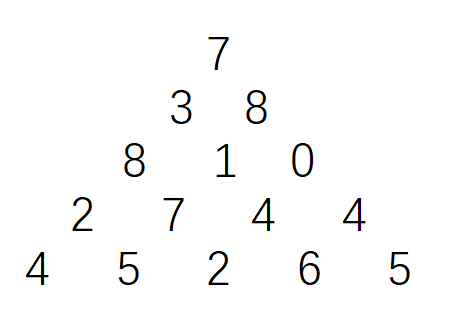动态规划

First Post:

Last Update:

动态规划（Dynamic Programming）

实验介绍

本节课我们进入动态规划课程的学习，动态规划是一种多阶段的决策过程最优化的问题。

本课程对于算法学习非常重要，但是又比较难，我们讲解分 $3$ 个章节进行动态规划问题的讲解。

今天的课程是动态规划系列的第一个章节。

知识点

  • 动态规划的基本思想
  • 动态规划问题的基本套路与步骤

为什么使用动态规划算法

我们先回忆一下贪心问题。

贪心又称贪婪算法。是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而使得问题得到全局最优解。

它的特点：

贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。

这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。

贪心选择性质就是，该问题的每一步选择都在选择最优的情况下能够导致最终问题的答案也是最优。

其实贪心和动态规划的区别，你可以理解为一个是正推，一眼就能看出来最优子结构，依次按照最优子结构选择每个过程最优选择即可。

而动态规划是没办法按照题目的意思直接得到最有优子结构，如下文所述:

多阶段决策过程最优化问题

动态规划问题，是运筹学的一个分支，动态规划主要用于求解以时间划分阶段的动态过程的优化问题。

在实际生活中，动态规划问题与贪心问题相似，都是完成某一事件的过程可以划分成多个阶段。

但是与贪心不同的是动态规划的每个状态之间都会相互影响和相互干涉，也就是说在某一阶段做出的决策会影响整个事件的最终结果。

因为阶段是有先后的，所以某一阶段的选取受之前阶段的影响，他也会影响后面的阶段。

多阶段决策问题：

多阶段决策过程问题，就是一类在每一阶段都需要做出选择，且某一阶段的决策受前面所有阶段决策后的状态影响，他的决策又会影响后续的决策。

这样一类问题就是多阶段决策问题。

多阶段决策过程最优化问题：

在多阶段决策问题中，各个阶段采取的决策，通常与时间相关，但有时又与其他的线性的变量相关。

我们前面说到，某个阶段的决策是在前面做完了的决策引发的某一个状态开始进行决策的。

而现在做的决策又会使得状态进行转移，那么又影响了下次进行决策的状态。

所以说作决策时的状态是动态的，规划是解决最优化问题的方式，所以解决这种多阶段决策过程最优化的方法叫做动态规划。

动态规划中的术语解释

  • 阶段： 把所给求解问题的过程恰当地分成若干个相互联系的阶段，以便于求解，过程不同，阶段数就可能不同

  • 状态： 述事物的性质，不同事物有不同的性质，因而用不同的状态来刻画。对问题的求解状态的描述是分阶段的

  • 决策： 根据题意要求，对每个阶段所做出的某种选择性操作

  • 策略： 由每个阶段的决策组成的序列称为策略

  • 状态转移方程： 用数学公式描述与阶段相关的状态间的演变规律

能采用动态规划求解的问题的性质

  • 最优化原理：

    如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

  • 无后效性：

    即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

  • 有重叠子问题：

    即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

解题步骤

  • 拆分问题
  • 定义状态(并找出初状态)
  • 找到状态转移
  • 逆推找最优子结构
  • 写出 DP 状态转移方程。

一般的模型方法

  • 递归搜索法
  • 记忆化搜索(记忆化暴力)
  • 递推式法

经典例题数塔问题

我们先来回顾一下我们之前讲过的数塔问题：

题目描述:

图片描述

如图数字三角形。如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径，使该路径所经过的数字总和最大。只要求输出总和。

  1. 一步可沿左斜线向下或右斜线向下走；
  2. 三角形行数小于等于 $100$；
  3. 三角形中的数字为 $0，1，…，99$；

测试数据通过键盘逐行输入。

如上例数据应以样例所示格式输入：

样例:

1
2
3
4
5
6
7
8
输入：

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
1
2
3
输出：

30

运行限制:

1
1. 最大运行时间：1s 2. 最大运行内存：128M

题目分析:

  1. 定义状态 假设 dp[i][j] 为处理 a[i][j] 后能达到的最大值。

  2. 找出状态转移

    dp[i][j]怎么转移呢？按照题意他有两条路径可以转移

    dp[i+1][j]=dp[i][j]+a[i+1][j] 向下走

    dp[i+1][j+1]=dp[i][j]+a[i+1][j+1] 向右下走

    我们有办法知道这两条路径哪条更优吗？

    不能！因为通向了两个不同的决策过程。为什么贪心可以知道，因为贪心处理完之后通向的是同一个决策过程，这里dp[i+1][j]和dp[i+1][j+1]明显他们两个所能达到的状态是完全不同的，这就是动态规划和贪心的不同之处。

    那我们怎样处理呢，我们要做的就是达到同一个状态我们才能够判断那个是最优的，这就是最优子结构。

  3. 逆推找最优子结构

    虽然我们进行了逆推，但是实际上不是因为我们逆推做了什么，只是因为我们找最优子结构的过程中恰好做了逆推的过程。

    我们要找最优子结构，我们刚才说了，要找到达同一状态的转移才能比较。那我们就考虑什么状态能够转移得到dp[i][j]，这时候我们直接看也能看出来是这两条路径dp[i+1][j]+a[i][j],dp[i+1][j+1]+a[i][j]。

  4. 写出状态转移方程

$dp[i][j] = max{dp[i+1][j]+a[i][j],dp[i+1][j+1]+a[i][j]}$

空间优化，已知 dp[i][j] 的值只会被覆盖前使用一次，所以可以合并 dp[i][j] 和 a[i][j] 那么就变成了。

$a[i][j] = max{a[i][j]+a[i+1][j],a[i][j]+a[i+1][j+1]}$

则 逆推到出发点 a[1][1] 为题目所求答案，即第一层到第 N 层的最大值。

答案解析：

C++ 解题代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>
using namespace std;

int main()
{
    int n; //n层
    int a[101][101]; //路径矩阵
    cin>>n;

    //输入数字三角形的值
    for (int i=1; i<=n; i++)
    {
        for (int j=1; j<=i; j++)
        {

        cin>>a[i][j]; //输入原始数据

        }
    }

    //递推开始

    for (int i=n-1; i>=1; i--)//从最后一层逆推
    {
        for (int j=1; j<=i; j++)
        {

            if (a[i+1][j]>=a[i+1][j+1])
                a[i][j]+=a[i+1][j];     //路径选择

            else
                a[i][j]+=a[i+1][j+1];
        }
    }

    cout<<a[1][1]<<endl;
}

Python 解题代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
a = [[0] * 101] * 101

if __name__ == '__main__':

  n = int(input())

  # 输入数字三角形的值
  for i in range(1, n+1):
      a[i] = input().split()
      a[i] = list(map(int, a[i]))  # split 分割后都是 字符 这里是转化成数字
  #
  # for i in range(1, n + 1):
  #     print(a[i])

 # a = list(map(int, a)) # split 分割后都是 字符 这里是转化成数字

  # 递推开始

  for i in range(n - 1, 0, -1):
      # 最后一层逆推
      for j in range(0, i):

          # 路径选择
          if a[i + 1][j] >= a[i + 1][j + 1]:
              a[i][j] += a[i + 1][j]

          else:
              a[i][j] += a[i + 1][j + 1]

  # for i in range(1, n + 1):
  #     print(a[i])

  print(a[1][0])

Java 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
package com.company;
import java.util.Scanner;

public class Main {

  static int [][]a=new int [101][101];

  public static void main(String[] args) {

      int n;
      Scanner in = new Scanner(System.in);
      n = in.nextInt();

      //输入数字三角形的值
      for (int i=1; i<=n; i++)
      {
          for (int j=1; j<=i; j++)
          {
              a[i][j]=in.nextInt(); //输入原始数据
          }
      }

      //递推开始

      for (int i=n-1; i>=1; i--)//从最后一层逆推
      {

          for (int j=1; j<=i; j++)
          {
              if (a[i+1][j]>=a[i+1][j+1])
                  a[i][j]+=a[i+1][j];     //路径选择

              else  a[i][j]+=a[i+1][j+1];
          }
      }
      System.out.println(a[1][1]);
  }
}

其实我们在讲这道题目中所用到的思想就是动态规划。

我们换种方式在理解一遍。

在用动态规划考虑数塔问题时可以自顶向下的分析，自底向上的计算。

从顶点出发时到底向左走还是向右走应取决于是从左走能取到最大值还是从右走能取到最大值，只要左右两道路径上的最大值求出来了才能作出决策。

同样的道理下一层的走向又要取决于再下一层上的最大值是否已经求出才能决策。

这样一层一层推下去，直到倒数第二层时就非常明了。

所以第一步对第五层的 $8$ 个数据，做如下四次决策：

  • 如果经过第四层 $2$，则在第五层的 $4$ 和 $5$ 中，决策选择的肯定是 $19$

  • 如果经过第四层 $7$，则在第五层的 $5$ 和 $2$ 中，决策选择的肯定是 $10$

  • 如果经过第四层第一个 $4$，则在第五层的 $2$ 和 $6$ 中，决策选择的肯定是 $6$

  • 如果经过第四层第二个 $4$，则在第五层的 $6$ 和 $5$ 中肯定是 $6$

经过一次决策，问题降了一阶。$5$ 层数塔问题转换成 $4$ 层数塔问题，经过如此的决策，就将原来问题转换为一阶数塔问题。

于是我们可以用我们上面的递推求解。

这就是递推式法模型。

我们通过这道简单的例题，大家首先要去找感觉，去分解问题的状态，去找决策，去找状态转移，而笔者认为动态规划问题，感觉是最重要的。

有的人 $10$ 道题就能找到感觉，有的人 $100$ 道题也找不到感觉。

游戏中的学问

难度: 简单 标签: DP, JSOI, 2013

题目链接：https://www.lanqiao.cn/problems/1436/learning/

题目描述：

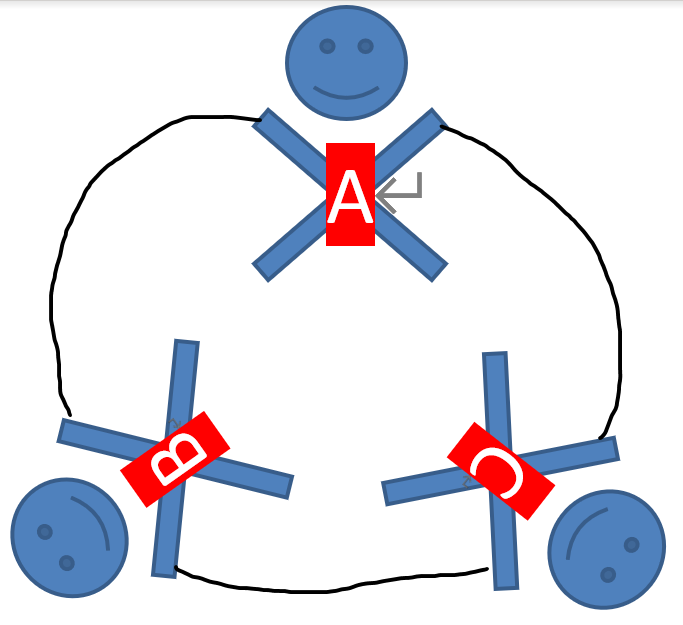
大家应该都见过很多人手拉手围着篝火跳舞的场景吧？

一般情况下，大家手拉手跳舞总是会围成一个大圈，每个人的左手拉着旁边朋友的右手，右手拉着另一侧朋友的左手。

不过，如果每一个人都随机的拉住两个不同人的手，然后再慢慢散开，事情就变得有趣多了——此时大家依旧会形成圈，不过却可能会形成多个独立的圈。

当然这里我们依然要求一个人的右手只能拉另一个人的左手，反之亦然。

班里一共有 $N$ 个同学，由 $1$ 到 $N$ 编号。Will 想知道，究竟有多少种本质不同的拉手方案，使得最终大家散开后恰好形成 $k$ 个圈呢？

给定两种方案，若存在一个人和他的一只手，满足在这两种方案中，拉着这只手的人的编号不同，则这两种方案本质不同。

输入描述：

1
2
3
4

输入一行包含三个正整数 N k P

3<=3k<=N<=3000，10^4<=p<=2×10^9

输出描述：

输出一行一个整数，表示本质不同的方案数对 p 的余数。保证 p 一定是一个质数。

输入输出样例：

  • 样例 1： Input：

    1
    2

    3 1 1000000009

    output：

    1
    2

答案解析：

题目是说随即的拉住右手，共计 N 个人形成 k 个独立环的可能的情况有多少种。

我们举个例子，A B C 三个人：

图片描述

A 的左手是 C A 的右手是 B B 的左手是 A B 的右手是 C C 的左手是 B C 的右手是 A

图片描述

A 的左手是 B A 的右手是 C B 的左手是 C B 的右手是 A C 的左手是 A C 的右手是 B

这两种是不同的。

最后对 P 取模。

这道题目可以说是记忆化搜索，也可以说是递推法模型。

定义状态：

我们设 dp{i,j} 是 i 个人组成 j 个圈有多少种情况的状态

找初始状态：

由于最少是三个人围成 1 个圈

所以 dp{3,1}=2

找状态转移：

我们考虑 dp{4,1} 的时候： 由于一开始三个人之间共计 3 个空位置，它可以见缝插针，所以就有 $3 \times$ dp {$3,1$}，dp{$4,1$} = $3 \times$ dp{$3,1$}

接着考虑 dp{x+1,y} 和 dp{x,y} 的关系：

假设 X 个人分成了 y 个环后每个环得人数是 X1 X2 ... Xy

对于第一个环 X1 来说共有 X1 个空

对于第二个环 X2 来说共有 X2 个空

共计 X1+X2+...+Xy=X

所以共有 X 个空，那么第 X+1 个人就用 X 种选择可以做。

所以 dp{$x+1,y$} = $x \times$ dp{$x,y$}，即 dp{$i,j$}=$(i-1) \times$ dp{$i-1,j$}

考虑 dp{$6,1$} 和 dp{$6,2$} ：

大家考虑以下我们划分阶段得方式是什么，是圈数吗？

如果是圈数，我们发现好像{$6,1$} 和 {$6,2$} 两个状态之间没有什么关系？

单纯的圈数不存在关系。

我们思考一下，至少需要 3 个人才能组成一个圈。

所以第 i 个人加入时，要在前 i-1 个人中抽出两个人才能组成一个新圈。

所以原本的 dp{$i-1,j$} 的状态就变成了，dp{$i-3,j$}了。

由于是从 i-1 个人中抽出 2 个人所以，共计$C_{i-1}^{2}$的抽取方式，3 个人我们已知能组成两种方案。

根据组合数求方案数的方式

$2\times C_{i-1}^{2}=2\times \frac{(i-1)!}{(i-3)!\times2}$

$2\times C_{i-1}^{2}=(i-1)!/(i-3)!=(i-1)*(i-2)$

所以 dp{i,j+1}=dp{i-3,j}×(i-1)×(i-2)

即 dp{i,j}=dp{i-3,j-1}×(i-1)×(i-2)

就此我们得到状态转移方程

  • dp{i,j}=dp{i-1,j}×(i-1)
  • dp{i,j}=dp{i-3,j-1}×(i-1)×(i-2)

除此之外，我们还有要考虑的情况，即建不建立新圈都是 dp{i,j}的情况，所以这里不是等于，而是求和:

dp{i,j}=dp{i-1,j}×(i-1)

dp{i,j}=dp{i,j}+dp{i-3,j-1}×(i-1)×(i-2)

比如：

dp{7,2}可以由 dp{6,2}转移而来

dp{7,2}也可以由 dp{4,1}转移而来

为什么这两种情况没有重叠，而是绝对异构的：

dp{6,2}由 dp{3,1}转移而来

dp{4,1}由 dp{3,1}转移而来

dp{4,1}中 1-4 号是在同一个圈内的。

dp{6,2}中 两个圈中的任意 3 个在一个圈内

不可能出现 1-4 在一个圈里的这种情况。

所以推导 dp{i,j}

dp{i,j}由 dp{i-i,j}转移而来 dp{i,j}也可以由 dp{i-3,j-1} 转移而来

dp{i-i,j}可以由 dp{i-2,j}或者 dp{i-4,j-1} dp{i-3,j-1}可以由 dp{i-4,j-1}或者 dp{i-6,j-2}

最终还是会到 3,1。

所以通过 3，通过两种方式走向了完全不同的方向。

至此我们轻松写出代码。

C++ 描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;
LL DP[3100][3100],mod;
int n,k;
int main()
{
    cin>>n>>k>>mod;
    DP[3][1]=2;
    for(int i=4;i<=n;i++)
    {

        for(int j=1;3*j<=i&&j<=k;j++)
        {
            DP[i][j]=DP[i-1][j]*(i-1)%mod;

            DP[i][j]=(DP[i][j]+DP[i-3][j-1]*(i-1)*(i-2))%mod;
        }
    }
    cout<<DP[n][k];
    return 0;
}

Python 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

n, k, mod = map(int, input().split())

DP=[[0 for i in range (3100)] for j in range (3100) ]

DP[3][1]=2

for i in range(4,n+1):

    for j in range(1,k+1):

        if 3*j>i:
            break

        DP[i][j]=DP[i-1][j]*(i-1)%mod

        DP[i][j]=(DP[i][j]+DP[i-3][j-1]*(i-1)*(i-2))%mod


print(DP[n][k])

java 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static long DP[][]=new long [3100][3100];

    public static int n,k;

 public static void main (String[] args) throws java.lang.Exception
 {
     Scanner in = new Scanner(System.in);

     n=in.nextInt();

     k=in.nextInt();

    long mod=in.nextLong();

     DP[3][1]=2;
        for(int i=4;i<=n;i++)
        {

            for(int j=1;3*j<=i&&j<=k;j++)
            {
                DP[i][j]=DP[i-1][j]*(i-1)%mod;

                DP[i][j]=(DP[i][j]+DP[i-3][j-1]*(i-1)*(i-2))%mod;
            }
        }
  System.out.println(DP[n][k]);
 }
}

跳跃

难度: 简单 标签: 动态规划, 搜索, 2021, 模拟赛

题目链接：https://www.lanqiao.cn/problems/553/learning/

题目描述： 开始时，小蓝站在方格图的左上角，即第 $1$ 行第 $1$ 列。

小蓝可以在方格图上走动，走动时，如果当前在第 $r$ 行第 $c$ 列，他不能走到行号比 $r$ 小的行，也不能走到列号比 $c$ 小的列。

同时，他一步走的直线距离不超过 $3$。

例如，如果当前小蓝在第 $3$ 行第 $5$ 列，他下一步可以走到

第 $3$ 行第 $6$ 列 第 $3$ 行第 $7$ 列 第 $3$ 行第 $8$ 列 第 $4$ 行第 $5$ 列 第 $4$ 行第 $6$ 列 第 $4$ 行第 $7$ 列 第 $5$ 行第 $5$ 列 第 $5$ 行第 $6$ 列 第 $6$ 行第 $5$ 列 小蓝最终要走到第 $n$ 行第 $m$ 列。

在图中，有的位置有奖励，走上去即可获得，有的位置有惩罚，走上去就要接受惩罚。奖励和惩罚最终抽象成一个权值，奖励为正，惩罚为负。

小蓝希望，从第 $1$ 行第 $1$ 列走到第 $n$ 行第 $m$ 列后，总的权值和最大。请问最大是多少？

输入描述：

输入的第一行包含两个整数 $n, m$，表示图的大小。

接下来 $n$ 行，每行 $m$ 个整数，表示方格图中每个点的权值。

其中，$1\leq n\leq 100$，$-10^4\leq$权值$\leq 10^4$。

输出描述：

输出一个整数，表示最大权值和。

输入输出样例：

  • 样例 1： Input：

    1
    2
    3
    4
    5

    3 5
    -4 -5 -10 -3 1
    7 5 -9 3 -10
    10 -2 6 -10 -4

    output：

    1
    2

    15

运行限制:

  • 最大运行时间：1s
  • 最大运行内存: 128M

答案解析：

由于这道题目数据较弱，大家可以使用搜索把所有情况都搜索到，每次到终点就保存最大值，知道遍历完所有的情况，然后输出最大值。

大家一定要写一遍 DFS 然后在看后边的 DP ,有时动态规划要从状态出发，有时动态规划又可以看成暴力搜索的剪枝。

我们先看一下搜索的解法：

因为只能向右下方移动，不存再走回头路的情况，所以不需要设置 Vis 数组。

C++ 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
#define MAX 105
using namespace std;
int n, m, sum = -0x3f3f3f3f;
int map[MAX][MAX];
int nextt[9][2] = { {0,1},{1,0},{0,2},{2,0},{0,3},{3,0},{1,1},{1,2},{2,1} };
void dfs(int x, int y,int value)
{
    value += map[x][y];
    if (x == n && y == m)
    {
        sum=max(sum,value);
        return;
    }

    for (int i = 0; i < 9; i++)
    {
        int tx = x + nextt[i][0];
        int ty = y + nextt[i][1];
        if (tx <= n && ty <= m)
            dfs(tx, ty, value);
    }
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> map[i][j];
    dfs(1, 1, 0);
    cout << sum;
    return 0;
}

Python 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


import os
import sys

# 请在此输入您的代码
n,m = map(int,input().strip().split())

mapTable = [list(map(int,input().strip().split())) for i in range(n)]

nextt = [[0,1],[0,2],[0,3],[1,0],[2,0],[3,0],[1,1],[1,2],[2,1]] #9种走的方式

Sum=float('-inf')

def dfs(x,y,value):

    global Sum

    value+=mapTable[x][y]
    if x==n-1 and y==m-1 :
        Sum=max(Sum,value)
        return

    for i in range(9):
        tx = x+nextt[i][0]
        ty = y+nextt[i][1]
        if  tx<n and  ty<m :

            dfs(tx,ty,value)
dfs(0,0,0)
print(Sum)

Java 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


import os
import sys

# 请在此输入您的代码
n,m = map(int,input().strip().split())

mapTable = [list(map(int,input().strip().split())) for i in range(n)]

nextt = [[0,1],[0,2],[0,3],[1,0],[2,0],[3,0],[1,1],[1,2],[2,1]] #9种走的方式

Sum=float('-inf')

def dfs(x,y,value):

    global Sum

    value+=mapTable[x][y]
    if x==n-1 and y==m-1 :
        Sum=max(Sum,value)
        return

    for i in range(9):
        tx = x+nextt[i][0]
        ty = y+nextt[i][1]
        if  tx<n and  ty<m :

            dfs(tx,ty,value)
dfs(0,0,0)
print(Sum)

我们再来看一下 DP 怎么解这个问题。

定义状态：

我们设 dp{$i,j$} 当走到第 $i$ 行第 $j$ 列的值。

找初始状态：

dp{$1,1$}

找状态转移：

对于dp{$i,j$} 会有 $9$ 种不同的状态转移，我们很难知道当前的选择去怎样影响后续的值，这就是上边的搜索问题，我们难以找到一种 DP 思路去求解这个问题，但是我们反向考虑，既然dp{$i,j$} 会有 $9$ 种转移方式，那么当这 $9$ 种状态的值为从这九种状态到达终点的最优解（最大值）时，那么我们就能轻易得到dp{$i,j$} 的最大值为这九种最优解的最大值。

继续消解子问题，那么我们得到这 $9$ 种最优子状态，继续根据同样的原理得到这 $9$ 种最优的子状态的最优子状态。

持续消解，发现只有到了 dp{$n,m$} 采用终止，这就是一个递归的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

value[n+5][m+5]

dp(x,y)
{
    if(x==n&&y==m)
        return value[n][m]

    if(越界)
        return 负无穷

    value[x][y]=value[x][y]+max(dp(x+1,y)......,dp(2,1))
    return dp(x,y)

}

这个过程是正推，根据递归写出递推来就变成了逆推，其实并不是根据动态规划写出来的逆推式，而是用正推递归变递推变来的，当然有的同学一眼看出来，那是非常优秀的。

这个题目数据量较小，用递归写不会爆，大家可以根据我的伪代码写写试试。

正推也是可以写出递推式，大家有兴趣可以尝试下。

C++ 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<iostream>
#define MAX 105
using namespace std;
int n, m, sum = -0x3f3f3f3f;
int map[MAX][MAX];
int nextt[9][2] = { {0,1},{1,0},{0,2},{2,0},{0,3},{3,0},{1,1},{1,2},{2,1} };

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> map[i][j];

    for(int i=n;i>=1;i--)
    {
      for(int j=m;j>=1;j--)
      {
        if(i==n&&j==m) continue;
        int maxTemp=-0x3f3f3f3f;
        for (int k = 0; k < 9; k++)
        {
          int tx = i + nextt[k][0];
          int ty = j + nextt[k][1];
          if (tx > n || ty > m) continue;
          maxTemp=max(maxTemp,map[tx][ty]);
        }
        map[i][j]+=maxTemp;
      }
    }
        // for (int i = 1; i <= n; i++){
        //   for (int j = 1; j <= m; j++)
        //   cout << map[i][j]<<" ";

        //   cout<<endl;
        // }
          cout << map[1][1];
    return 0;
}

Python 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
nextt = [[0, 1], [0, 2], [0, 3], [1, 0], [2, 0], [3, 0], [1, 1], [1, 2], [2, 1]]  # 9种走的方式

n, m = map(int, input().split())

DP = [list(map(int, input().split())) for i in range(n)]

for i in range(n - 1, -1, -1):
    for j in range(m - 1, -1, -1):
        if i == n - 1 and j == m - 1:
            continue

        maxTemp = float('-inf')

        for k in range(9):
            tx = i + nextt[k][0]
            ty = j + nextt[k][1]

            if tx >= n or ty >= m:
                continue

            maxTemp = max(maxTemp, DP[tx][ty])

        DP[i][j] += maxTemp

print(DP[0][0])

java 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

import java.io.*;
import java.util.Scanner;
public class test
{

    public static int n, m, Sum = -0x3f3f3f3f;

    public static int [][] mapTable=new int [105][105];

    public static int nextt[][] ={ {0,1},{1,0},{0,2},{2,0},{0,3},{3,0},{1,1},{1,2},{2,1} };



 public static void main (String[] args) throws java.lang.Exception
 {

      Scanner in =new Scanner(System.in);
      n=in.nextInt();
      m=in.nextInt();
     for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                    mapTable[i][j]=in.nextInt();

    for(int i=n;i>=1;i--)
    {
      for(int j=m;j>=1;j--)
      {
        if(i==n&&j==m) continue;
        int maxTemp=-0x3f3f3f3f;

        for (int k = 0; k < 9; k++)
        {
          int tx = i + nextt[k][0];
          int ty = j + nextt[k][1];
          if (tx > n || ty > m) continue;
          maxTemp=Math.max(maxTemp,mapTable[tx][ty]);
        }
        mapTable[i][j]+=maxTemp;
      }
    }

  System.out.println(mapTable[1][1]);
 }
}

动态规划背包问题

实验介绍

本节课我们进入动态规划课程的学习，动态规划是一种多阶段的决策过程最优化的问题。

本课程对于算法学习非常重要，但是又比较难，我们讲解分 $3$ 个章节进行动态规划问题的讲解。

今天的课程是动态规划系列的第二个章节。

知识点

  • 0-1 背包
  • 完全背包
  • 多重背包问题

背包问题

我们上一章课程讲解了动态规划算法的基本原理，包括动态规划的“为什么使用动态规划算法”、“多阶段决策过程最优化问题”、“动态规划中的术语解释”，“可解动态鬼规划的性质”等知识点。

今天我们来讲一下，动态规划中的背包问题，背包问题，是比赛中常考的问题，也是动态规划入门的问题，其实动态规划并没有套路，只是这类问题有着明确的特点，如果你做的题足够多的话，你会发现很多问题都会有模板。

背包问题基本都是不可拆分背包，因为可拆分背包是贪心去求解的问题。我们今天讲三种背包的基本模型：1.0-1 背包、2.完全背包、3.多重背包问题。

0-1 背包问题

0-1 背包是背包问题的入门的问题。但是背包问题的模板也是最简单的。

0-1 背包的问题是什么呢？

其问题的简单表述为，有 N 件物品，每件物品只有一件。每个物品都有一个价值$w_i$，每件物品都有一个占一个部分空间$c_i$,已知你的背包共计可承重 C(Contains),现在让你求你的背包最多装得下多少$w_{Max}$，即求你背包中物品的最大价值$w_{Max}$。

对于这个问题我们有以下模板:

1.定义变量并输入

C++ 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 定义V,W用于保存价值和质量
#define Maxn 5000

int c[Maxn],w[Maxn];

int C;

// 输入

int n;

cin>> n;

for(int i=0;i<n;i++)
{
    cin>>c[i]>>w[i];
}

cin>>C;

//创建动态规划数组

int dp[Maxn];

Python 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import os
import sys

c = []
w = []
dp = []

if __name__ == '__main__':

    n, C = map(int, input().strip().split())

    for i in range(n):

        tempC, tempW = map(int, input().strip().split())

        c.append(tempC)

        w.append(tempW)

java 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import java.util.Arrays;
import java.util.Scanner;

import static java.lang.Math.max;

public  class  Main{

    static int []c;
    static int []w;
    static int dp[];

   static int C;

    static int n;

    public static void main(String[] args)
    {
        Scanner in = new Scanner(System.in);

        n=in.nextInt();

       C=in.nextInt();

       c=new int[n+50];

       w=new int[n+50];

       dp=new int [C+50];

        for (int i = 0; i < n; i++) {

             c[i]=in.nextInt();
             w[i]=in.nextInt();;
        }



    }
}

2.执行算法

我们先去找到状态转移方程

dp[i][j]=max(dp[i][j],dp[i−1]j−c[i]]+w[i])

含义，选到第 i 件物品，且背包现在重量为 j。

那么考虑这个状态会由什么状态转移而来，肯定是选到第 i-1 件的时候。

如果选了第 i 件，那么就是由 dp[i−1]j−c[i]]转移而来。

如果不选第 i 件，那么就是由 dp[i][j]转移而来。

那么已知 dp[i−1]j−c[i]]和 dp[i][j]都为各自最优的状态，那我们直接取最优状态即可。

C++ 描述：

1
2
3
4
5
6
7
8
9
10

for(int i=0;i<n;i++)
{

    for(int j=0;j<=C;j++)
    {
        if(j>=c[i])
            dp[i][j]=max(dp[i][j],dp[i-1][j-c[i]]+w[i]);
    }
}

Python 语言描述:

1
2
3
4
5
6
7
8

for i in range(n):

    for j in reversed(C+1):

        dp[i][j]=max(dp[i][j],dp[i-1][j-c[i]]+w[i])

print(dp[C])

Java 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14


for(int i=0;i<n;i++)
{

    for(int j=0;j<=C;j++)
    {
        if(j>=c[i])
            dp[i][j]=max(dp[i][j],dp[i-1][j-c[i]]+w[i]);
    }
}


        System.out.println(dp[C]);

空间优化：

因为状态转移每次只与上一层有关，所以用一个一维数组就可以。

为什么从大到小遍历， 看 $dp[j]=dp[j-c[i]]+w[i]$ 这一状态转移，是根据小的改大的，如果先把小的改了，那小的还会被用到，数据就不对了，所以从小到大。

C++ 描述；

1
2
3
4
for(int i=0;i<n;i++) //遍历每一件物品
    for(int j=C;j>=c[i];j--)
    //遍历背包容量，表示在上一层的基础上，容量为J时，第i件物品装或不装的最优解;
        dp[j]=max(dp[j-c[i]]+w[i],dp[j]);

Python 语言描述:

1
2
3
4
5
6
7

for i in range(n):

    for j in reversed(range(c[i],C+1)):
        dp[j] = max(dp[j - c[i]] + w[i], dp[j]);

print(dp[C])

Java 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12


for (int i = 0; i < n; i++) //遍历每一件物品
{

    for (int j = C; j >= c[i]; j--)
        //遍历背包容量，表示在上一层的基础上，容量为J时，第i件物品装或不装的最优解;
        dp[j] = max(dp[j - c[i]] + w[i], dp[j]);
}


System.out.println(dp[C]);

初始化细节：

  • 装满 $dp[0]=0$，其余赋值 $-INF$；
  • 不装满全初始化为 $0$；

C++ 语言描述：

1
2
3
4
5
6
7
8
9

//装满
memset(dp, 0, sizeof(dp));

dp[0]=0;

//不装满

memset(dp, -0x3f, sizeof(dp));

Python 语言描述:

1
2
3
4
5
6
7
8
9
10
11
# 装满
for i in range(C + 50):

    dp.append(-0x3f3f3f3f)

dp[0]=0

# 不装满
for i in range(C + 50):

    dp.append(0)

Java 语言描述：

1
2
3
4
5
6
7
8
9

//装满
Arrays.fill(dp, -0x3f3f3f3f);

dp[0]=0;

//不装满

memset(dp, -0x3f, sizeof(dp));

题目描述:

题目链接：https://www.lanqiao.cn/problems/1174/learning/

小明有一个容量为 $V$ 的背包。

这天他去商场购物，商场一共有 $N$ 件物品，第 $i$ 件物品的体积为 $w$ ，价值为 $v$，每种物品都只有一个。

小明想知道在购买的物品总体积不超过 $V$ 的情况下所能获得的最大价值为多少，请你帮他算算。

输入描述:

输入第 $1$ 行包含两个正整数 $N,V$，表示商场物品的数量和小明的背包容量。

第 $2∼N+1$ 行包含 $2$ 个正整数 $w,v$，表示物品的体积和价值。

样例:

1
2
3
4
5
6
7
8
输入：

5 20
1 6
2 5
3 8
5 15
3 3
1
输出： 37

运行限制:

1
1. 最大运行时间：1s 2. 最大运行内存：128M

答案解析：

C++ 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

#include <iostream>
#include <cstring>

using namespace std;
#define Maxn 5000


int c[Maxn], w[Maxn];
int dp[Maxn];
int C;

// 输入

int n;

int main() {

    cin >> n;

    cin >> C;

    for (int i = 0; i < n; i++) {

        cin >> c[i] >> w[i];
    }


    int dp[Maxn];

    memset(dp, 0, sizeof(dp)); //不装满

    //创建动态规划数组



    for (int i = 0; i < n; i++) //遍历每一件物品
    {

        for (int j = C; j >= c[i]; j--)
            //遍历背包容量，表示在上一层的基础上，容量为J时，第i件物品装或不装的最优解;
            dp[j] = max(dp[j - c[i]] + w[i], dp[j]);
    }

    cout << dp[C] << endl;

}

Python 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

c = []
w = []
dp = []

if __name__ == '__main__':

    n, C = map(int, input().strip().split())
    for i in range(n):
        tempC, tempW = map(int, input().strip().split())
        c.append(tempC)
        w.append(tempW)

    for i in range(C + 50):
        dp.append(0)

    for i in range(n):
        for j in reversed(range(c[i],C+1)):
            dp[j] = max(dp[j - c[i]] + w[i], dp[j]);

    print(dp[C])

Java 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

import java.util.Arrays;
import java.util.Scanner;

import static java.lang.Math.max;

public  class  Main{

    static int []c;
    static int []w;
    static int dp[];
    static int C;
    static int n;

    public static void main(String[] args)
    {
        Scanner in = new Scanner(System.in);

        n=in.nextInt();
        C=in.nextInt();
        c=new int[n+50];
        w=new int[n+50];
        dp=new int [C+50];

        for (int i = 0; i < n; i++) {

             c[i]=in.nextInt();
             w[i]=in.nextInt();;
        }

        Arrays.fill(dp, 0);

        for (int i = 0; i < n; i++) //遍历每一件物品
        {

            for (int j = C; j >= c[i]; j--)
                //遍历背包容量，表示在上一层的基础上，容量为J时，第i件物品装或不装的最优解;
                dp[j] = max(dp[j - c[i]] + w[i], dp[j]);
        }
        System.out.println(dp[C]);

    }
}

完全背包问题

完全背包是背包问题的入门的问题。

根据 0-1 背包写出模板也是很简单的。

完全背包的问题是什么呢？

其问题的简单表述为，有 $N$ 件物品，每件物品有无数件。每个物品都有一个价值$w_i$，每件物品都有一个占一个部分空间$c_i$,已知你的背包共计可承重 $C(Contains)$,现在让你求你的背包最多装得下多少$w_{Max}$，即求你背包中物品的最大价值$w_{Max}$。

对于这个问题我们有以下模板:

1.定义变量并输入

参考 0-1 背包。

2.执行算法

我们先去找到状态转移方程

dp[i][j]=max(dp[i][j],dp[i]j−c[i]]+w[i])

含义，选到第 $i$ 件物品，且背包现在重量为 $j$。

那么考虑这个状态会由什么状态转移而来，肯定是选到第 $i-1$ 件的时候,或者选了若干次第 $i$ 件。

如果不选第 $i$ 种，那么就是由 dp[i-1][j]转移而来。

如果选了第 $i$ 件，那么就是由 dp[i−1]j−c[i]]转移而来。

或者在某一刻，不在选第 $i$ 件了，那么就是有 dp[i][j]转移而来。

那么已知 dp[i]j−c[i]]和 dp[i][j]都为各自最优的状态，那我们直接取最优状态即可。

C++ 描述：

1
2
3
4
5
6
7
for(int i=0;i<n;i++){
    for(int j=0;j<=C;j++){
        dp[i][j]=dp[i-1][j];
        if(j>=c[i])  dp[i][j]=max(dp[i][j],dp[i][j-c[i]]+w[i]);
    }
}
cout<<dp[n][C]<<endl;

Python 语言描述:

1
2
3
4
5
for i in range(n):
    for j in range(C+1):
        dp[i][j]=dp[i-1][j];
        dp[i][j]=max(dp[i][j],dp[i][j-c[i]]+w[i])
print(dp[n][C])

Java 语言描述：

1
2
3
4
5
6
7
for(int i=0;i<n;i++){
    for(int j=0;j<=C;j++){
        dp[i][j]=dp[i-1][j];
        if(j>=c[i])dp[i][j]=max(dp[i][j],dp[i][j-c[i]]+w[i]);
    }
}
 System.out.println(dp[n][C]);

空间优化：

因为状态转移每次只与上一层有关，所以用一个一维数组就可以。

为什么从小到大遍历， 看 $dp[j]=dp[j-c[i]]+w[i]$ 这一状态转移，是根据小的改大的，而此时的含义为选了 x 件后的容量与质量，跟 01 背包类似，但含义不同，处理方式上也有本质区别，处理完一件后在处理下件。

C++ 描述；

1
2
3
4
for(int i=0;i<n;i++) //遍历每一件物品
    for(int j=c[i];j<=C;j++)
    //遍历背包容量，表示在上一层的基础上，容量为J时，第i件物品装或不装的最优解;
        dp[j]=max(dp[j-c[i]]+w[i],dp[j]);

Python 语言描述:

1
2
3
4
5
6
7

for i in range(n):

    for j in range(c[i],C+1):
        dp[j] = max(dp[j - c[i]] + w[i], dp[j]);

print(dp[C])

Java 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12


for (int i = 0; i < n; i++) //遍历每一件物品
{

    for(int j=c[i];j<=C;j++)
        //遍历背包容量，表示在上一层的基础上，容量为J时，第i件物品装或不装的最优解;
        dp[j] = max(dp[j - c[i]] + w[i], dp[j]);
}


System.out.println(dp[C]);

初始化细节：

与 0 - 1背包相同。

  • 装满 $dp[0]=0$，其余赋值$-INF$；
  • 不装满全初始化为 $0$；

题目描述:

题目链接：https://www.lanqiao.cn/problems/1175/learning/

小明有一个容量为 $V$ 的背包。

这天他去商场购物，商场一共有 $N$ 件物品，第 $i$ 件物品的体积为 $w$ ，价值为 $v$，每种物品都有无限多个。

xxxxxxxxxx68 1import java.io.*;2​3public class Main {4    static int N=110;5    static long[][] g=new long[N][N],m=new long[N][N],f=new long[N][N];6    static long n,q;7    static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));8    static PrintWriter  out=new PrintWriter(new OutputStreamWriter(System.out));9    public static void main(String[] args) throws IOException {10        String[] s=br.readLine().split(“ “);11        n=Long.parseLong(s[0]);12        q=Long.parseLong(s[1]);13        for(int i=1;i<=n;++i){14            s=br.readLine().split(“ “);15            for(int j=1;j<=n;++j){16                g[i][j]=Long.parseLong(s[j-1]);17           }18       }19        for(int i=1;i<=n;++i){20            s=br.readLine().split(“ “);21            for(int j=1;j<=n;++j){22                m[i][j]=Long.parseLong(s[j-1]);23                f[i][j]=m[i][j];24           }25       }26        if(floyd()>q){27            out.println(-1);28            out.flush();29            return;30       }31        long l=0,r=1000000000;32        while(l<r){33            long mid=l+r>>1;34            if(check(mid)) r=mid;35            else l=mid+1;36       }37        out.println(r);38        out.flush();39   }40    static long floyd(){41        long a=0;42        for (int k = 1; k <= n; k ++ )43            for (int i = 1; i <= n; i ++ )44                for (int j = 1; j <= n; j ++ )45                    f[i][j] =Math.min(f[i][j], f[i][k] + f[k][j]);46​47        for(int i=1;i<=n;++i)48            for(int j=1;j<=n;++j)49                a+=f[i][j];50        return a;51   }52    static boolean check(long x){53        for(int i=1;i<=n;++i){54            for(int j=1;j<=n;++j) f[i][j]=g[i][j];55       }56        long h=x/n;57        long s=x%n;58        for(int i=1;i<=n;++i){59            for(int j=1;j<=n;++j){60                if(i==j) continue;61                if(i<=s) f[i][j]=Math.max(m[i][j],f[i][j]-h-1);62                else f[i][j]=Math.max(m[i][j],f[i][j]-h);63                f[j][i]=f[i][j];64           }65       }66        return floyd()<=q;67   }68}java

输入描述:

输入第 $1$ 行包含两个正整数 $N,V$，表示商场物品的数量和小明的背包容量。

第 $2∼N+1$ 行包含 $2$ 个正整数 $w,v$，表示物品的体积和价值。

样例:

1
2
3
4
5
6
7
8
输入：

5 20
1 6
2 5
3 8
5 15
3 3
1
输出： 120

运行限制:

1
1. 最大运行时间：1s 2. 最大运行内存：128M

答案解析：

C++ 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

#include <iostream>
#include <cstring>

using namespace std;
#define Maxn 5000

int c[Maxn], w[Maxn];
int dp[Maxn];
int C;
// 输入

int n;
int main() {

    cin >> n;
    cin >> C;

    for (int i = 0; i < n; i++) {

        cin >> c[i] >> w[i];
    }

    int dp[Maxn];

    memset(dp, 0, sizeof(dp)); //不装满
    //创建动态规划数组

    for (int i = 0; i < n; i++) //遍历每一件物品
    {
        for(int j=c[i];j<=C;j++)
            //遍历背包容量，表示在上一层的基础上，容量为J时，第i件物品装或不装的最优解;
            dp[j] = max(dp[j - c[i]] + w[i], dp[j]);
    }
    cout << dp[C] << endl;

}

Python 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import os
import sys

c = []
w = []
dp = []

if __name__ == '__main__':

    n, C = map(int, input().strip().split())

    for i in range(n):
        tempC, tempW = map(int, input().strip().split())
        c.append(tempC)
        w.append(tempW)

    for i in range(C + 50):
        dp.append(0)

    for i in range(n):
        for j in range(c[i],C+1):
            dp[j] = max(dp[j - c[i]] + w[i], dp[j])

    print(dp[C])

Java 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import java.util.Arrays;
import java.util.Scanner;

import static java.lang.Math.max;

public  class  Main{

    static int []c;
    static int []w;
    static int dp[];
    static int C;
    static int n;

    public static void main(String[] args)
    {
        Scanner in = new Scanner(System.in);

        n=in.nextInt();
        C=in.nextInt();
        c=new int[n+50];
        w=new int[n+50];
        dp=new int [C+50];
        for (int i = 0; i < n; i++) {
             c[i]=in.nextInt();
             w[i]=in.nextInt();;
        }
        Arrays.fill(dp, 0);
        for (int i = 0; i < n; i++) //遍历每一件物品
        {
                for(int j=c[i];j<=C;j++)
                //遍历背包容量，表示在上一层的基础上，容量为J时，第i件物品装或不装的最优解;
                dp[j] = max(dp[j - c[i]] + w[i], dp[j]);
        }
        System.out.println(dp[C])
    }
}

多重背包

多重背包是背包问题的入门的问题。 根据 0-1 背包写出模板也是很简单的。

多重背包的问题是什么呢？

其问题的简单表述为，有 N 件物品，每件物品有$s_i$件。每个物品都有一个价值$w_i$，每件物品都有一个占一个部分空间$c_i$,已知你的背包共计可承重 C(Contains),现在让你求你的背包最多装得下多少$w_{Max}$，即求你背包中物品的最大价值$w_{Max}$。

对于这个问题我们有以下模板:

1.定义变量并输入

参考 0-1 背包。

2.执行算法

这次我们直接空间优化，不再讲解二维做法：

多重背包是可以不选，也可以选 1 个，可以选多个，而 0-1 背包只能选 0 个或者 1个。

那就直接把种物品分开，即可比如：

每个盘子 3 块钱，我有 2 个。每双筷子 1 块钱，我有 10 双，每对刀叉 3 块钱，我有 3 个。

那么我就可以拆成，有 2 个三块的盘子，每个可以选也可以不选，就变成了 0-1 背包。

也就是说，对于每种是可以选多个，那就直接拆分成独立的个体就可以了。

C++ 描述；

1
2
3
4
5
6
7
8
9
10
11
for(int i=0;i<n;i++)
//遍历每一个物品
    for(int j=0;j<=s[i];j++)
    //遍历物品的数量
        for(int k=C;k>=c[i];k--)
        //当做01背包来处理
        {
            //取01背包情况的dp[k]和dp[k-c[i]]+w[i]的最大值
            dp[k]=max( dp[k],dp[k-c[i]]+w[i] );
        }

Python 语言描述:

1
2
3
4
5
6
7

for i in range(n):
    for j in range(s[i]+1):
        for k in reversed(range(c[i],C+1)):
            dp[k]=max( dp[k],dp[k-c[i]]+w[i] )

print(dp[C])

Java 语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15


for(int i=0;i<n;i++)
//遍历每一个物品
    for(int j=0;j<=s[i];j++)
    //遍历物品的数量
        for(int k=C;k>=c[i];k--)
        //当做01背包来处理
        {
            //取01背包情况的dp[k]和dp[k-c[i]]+w[i]的最大值
            dp[k]=max( dp[k],dp[k-c[i]]+w[i] );
        }


System.out.println(dp[C]);

不顾这样做大概率会超时，我们换一种理解方式：

在这两种问题中，我们需要考虑每个物品选择取或不取的情况，通过动态规划来求解最优解。

$01$背包问题中，对于每个物品$i$，我们有两个选择：选取或不选取。状态转移方程为： $dp[j] = \max(dp[j], dp[j - v[i]] + w[i])$

多重背包问题中，对于每个物品i，我们可以选择取$0$个、$1$个、$2$个…直到$s[i]$个。状态转移方程为： $dp[j] = \max(dp[j], dp[j - v[i] \cdot k] + w[i] \cdot k)$ 其中，k 的取值范围是$0, 1, 2, …, s[i]$。

这两个问题的解决思路相似，都是通过填充一个二维的动态规划数组$dp$，其中$dp[j]$表示背包容量为j时的最优解。在状态转移时，我们考虑了每个物品的选择情况，求解最终的最优解。

初始化细节：

与 $0 - 1$ 背包相同。

  • 装满 $dp[0]=0$，其余赋值$-INF$；
  • 不装满全初始化为 $0$；

题目描述:

题目链接：https://www.lanqiao.cn/problems/1176/learning/

小明有一个容量为 $V$的背包。

这天他去商场购物，商场一共有 $N$ 件物品，第 $i$ 件物品的体积为 $w$，价值为 $v$，每种物品都有$s$个。

小明想知道在购买的物品总体积不超过 $V$ 的情况下所能获得的最大价值为多少，请你帮他算算。

输入描述:

输入第 $1$ 行包含两个正整数 $N,V$，表示商场物品的数量和小明的背包容量。

第 $2∼N+1$ 行包含 $3$ 个正整数 $w,vs$,表示物品的体积、价值和数量。

样例:

1
2
3
4
5
6
7
输入：

3 30
1 2 3
4 5 6
7 8 9

1
输出： 39

运行限制:

1
1. 最大运行时间：1s 2. 最大运行内存：128M

答案解析：

C++ 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

#include <iostream>
#include <cstring>

using namespace std;
#define Maxn 5000

int c[Maxn], w[Maxn], s[Maxn];
int dp[Maxn];
int C;

// 输入
int n;

int main() {

    cin >> n;
    cin >> C;
    for (int i = 0; i < n; i++) {
        cin >> c[i] >> w[i] >> s[i];
    }


    int dp[Maxn];
    memset(dp, 0, sizeof(dp)); //不装满

    //创建动态规划数组

    for (int i = 0; i < n; i++)
//遍历每一个物品
    {
        for(int j=C;j>=c[i];j--)
        {
            for(int k=1;k<=s[i] && j>=k*c[i];k++)
                //遍历物品的数量
                dp[j]=max(dp[j],dp[j-k*c[i]]+w[i]*k);
        }
    }

    cout << dp[C] << endl;

}

Python 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
c = []
w = []
s=[]
dp = []

if __name__ == '__main__':

    n, C = map(int, input().strip().split())

    for i in range(n):

        tempC, tempW ,tempS= map(int, input().strip().split())
        c.append(tempC)
        w.append(tempW)
        s.append(tempS)

    for i in range(C + 50):
        dp.append(0)

    for i in range(n):
        for j in reversed(range(c[i],C+1)):
            for k in range(s[i]+1):
                if j<k*c[i]:
                    break;
                dp[j] = max(dp[j], dp[j - k * c[i]] + w[i] * k)

    print(dp[C])

Java 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

import java.util.Arrays;
import java.util.Scanner;

import static java.lang.Math.max;

public  class  Main{

        static int []c;
        static int []w;
        static int []s;
        static int dp[];

        public static void main(String[] args)
        {
            Scanner in = new Scanner(System.in);
            int n=in.nextInt();
            int C=in.nextInt();
            c=new int[n+50];
            w=new int[n+50];
            s=new int[n+50];
            dp=new int [C+50];

            for (int i = 0; i < n; i++) {

                c[i]=in.nextInt();
                w[i]=in.nextInt();
                s[i]=in.nextInt();
            }

            Arrays.fill(dp, 0);
            for (int i = 0; i < n; i++)
//遍历每一个物品
            {
                for(int j=C;j>=c[i];j--)
                {
                    for(int k=1;k<=s[i] && j>=k*c[i];k++)
                        //遍历物品的数量
                        dp[j]=max(dp[j],dp[j-k*c[i]]+w[i]*k);
                }
            }

            System.out.println(dp[C]);


    }
}

动态规划线性 DP

实验介绍

本课程对于算法学习非常重要，但是又比较难，我们讲解分 $3$ 个章节进行动态规划问题的讲解。

今天的课程是动态规划系列的第 $3$ 个章节。

知识点

  • 讲解很多经典的动态规划问题，对动态规划初步掌握。

普通线性 DP

线性 DP 是动态规划问题中的一类问题，指状态之间有线性关系的动态规划问题。

这类问题不像是我们讲的背包等问题有固定的模板。

少数常见的线性 DP 问题也有模板，比如我们讲的 $LIS$ 和 $LCS$ 问题。

大部分还是需要根据题目进行推导，基本没有什么规律可循。

大部分线性规划的问题，都需要自己首先定义状态，找到决策，推导状态转移方程。

我们再讲解几个题目，让大家找找做最普遍 DP 问题的感觉。

蓝肽子序列

题目链接：蓝肽子序列

题目描述:

L 星球上的生物由蛋蓝质组成，每一种蛋蓝质由一类称为蓝肽的物资首尾连接成一条长链后折叠而成。

生物学家小乔正在研究 L 星球上的蛋蓝质。她拿到两个蛋蓝质的蓝肽序列，想通过这两条蓝肽序列的共同特点来分析两种蛋蓝质的相似性。

具体的，一个蓝肽可以使用 $1$ 至 $5$ 个英文字母表示，其中第一个字母大写，后面的字母小写。一个蛋蓝质的蓝肽序列可以用蓝肽的表示顺序拼接而成。

在一条蓝肽序列中，如果选取其中的一些位置，把这些位置的蓝肽取出，并按照它们在原序列中的位置摆放，则称为这条蓝肽的一个子序列。蓝肽的子序列不一定在原序列中是连续的，中间可能间隔着一些未被取出的蓝肽。

如果第一条蓝肽序列可以取出一个子序列与第二条蓝肽序列中取出的某个子序列相等，则称为一个公共蓝肽子序列。

给定两条蓝肽序列，找出他们最长的那个公共蓝肽子序列的长度。

输入描述:

输入两行，每行包含一个字符串，表示一个蓝肽序列。字符串中间没有空格等分隔字符。

其中有 ，两个字符串的长度均不超过 $1000$。

输出描述:

输出一个整数，表示最长的那个公共蓝肽子序列的长度。

输入输出样例:

示例:

输入

1
LanQiaoBei LanTaiXiaoQiao

输出

1
2

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

答案解析：

该题目是 $LCS$ 的变形，由原来的一个字符或者一个数字的匹配变成了，一个单词的匹配。

这个题目为先划分字符串变成基本的比较单位。

然后再套用 $LCS$ 模板

即可完成这道题目。

C++ 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <algorithm>
using namespace std;
int dp[1005][1005];
string s1, s2;
string a[1005], b[1005];
int n=0, m=0;
int main()
{
    cin >> s1 >> s2;
    int d1 = s1.length(), d2 = s2.length();
    for (int i = 0; i < d1;)
    {
        if (s1[i] >= 'A' && s1[i] <= 'Z')
        {
            a[n] += s1[i++];
            while (s1[i] >= 'a' && s1[i] <= 'z')
            {
                a[n] += s1[i++];
            }
        }
        n++;
    }
    for (int i = 0; i < d2;)
    {
        if (s2[i] >= 'A' && s2[i] <= 'Z')
        {
            b[m] += s2[i++];
            while (s2[i] >= 'a' && s2[i] <= 'z')
            {
                b[m] += s2[i++];
            }

        }
        m++;
    }
     dp[0][0] = 0;

    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
        {

            if (a[i] == b[j])
            {
                dp[i + 1][j + 1] = dp[i][j] + 1;
            }
            else
            {
                dp[i + 1][j + 1]=max(dp[i + 1][j], dp[i][j + 1]);
            }
        }
    cout << dp[n][m] << endl;
}

Python 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
Maxn = 1005
dp = [[0 for _ in range(Maxn)] for _ in range(Maxn)]

if __name__ == '__main__':

    s1 = input()
    s2 = input()
    a = []
    b = []
    temp = ''

    for word in s1:
        if 'A' <= word <= 'Z':
            if temp != '':
                a.append(temp)
            temp = ''
        temp += word
    a.append(temp)

    temp = ' '

    for word in s2:
        if 'A' <= word <= 'Z':
            if temp != '':
                b.append(temp)
            temp = ''
        temp += word
    b.append(temp)

    n = len(a)
    m = len(b)

    for i in range(len(a)):
        for j in range(len(b)):
            if a[i] == b[j]:
                dp[i + 1][j + 1] = dp[i][j] + 1

            else:
                if dp[i + 1][j] > dp[i][j + 1]:
                    dp[i + 1][j + 1] = dp[i + 1][j]

                else:
                    dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1])

    print(dp[n][m])

Java 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
import java.util.Scanner;

public class Main {


    static int[][] dp;
    static String s1;
    static String s2;
    static String []a;
    static String []b;

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);

        int n=0,m=0;

        s1=in.next();
        s2=in.next();

        a=new String[1005];
        b=new String[1005];

        int d1=s1.length();
        int d2=s2.length();

        dp=new int[1005][1005];

        for (int i = 0; i < d1;n++)
        {


            if (s1.charAt(i) - 'A'>=0 && s1.charAt(i) - 'Z'<=0)
            {
                a[n] += s1.charAt(i++);
                while (i < d1&&s1.charAt(i) -'a'>=0 && s1.charAt(i)-'z' <=0)
                {
                    a[n] += s1.charAt(i++);
                }

            }

        }
        for (int i = 0; i < d2;m++)
        {

            if (s2.charAt(i) - 'A'>=0 && s2.charAt(i) - 'Z'<=0)
            {
                b[m] += s2.charAt(i++);
                while (i < d2&&s2.charAt(i) -'a'>=0&& s2.charAt(i)-'z' <= 0)
                {
                    b[m] += s2.charAt(i++);
                }

            }

        }
        dp[0][0] = 0;

        int Maxn=Math.max(n,m)+50;
        dp=new int[Maxn][Maxn];
        dp[0][0]=0;

        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
            {
                if (a[i].equals( b[j]))
                {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                }
                else
                {
                    dp[i + 1][j + 1]=Math.max(dp[i + 1][j], dp[i][j + 1]);
                }
            }
        System.out.println(dp[n][m]);

    }
}

合唱队形

题目链接：https://www.lanqiao.cn/problems/742/learning/

题目描述:

$N$ 位同学站成一排，音乐老师要请其中的 $(N-K)$ 位同学出列，使得剩下的 $K$ 位同学排成合唱队形。

合唱队形是指这样的一种队形：设 $K$ 位同学从左到右依次编号为 $1，2，\cdots K$，他们的身高分别为 $T_1，T_2，\cdots，T_K$， 则他们的身高满足 $T_1< \cdots < T_i> T_{i+1}> \cdots >T_K(1 \leq i \leq K)$。

你的任务是，已知所有 $N$ 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入描述:

输入两行。

第一行是一个整数 $N\ (2 \leq N \leq 100)$，表示同学的总数。

第二行有 $n$ 个整数，用空格分隔，第 $i$ 个整数 $T_i(130 \leq T_i \leq 230)$ 是第 $i$ 位同学的身高(厘米)。

输出描述:

输出一个整数，就是最少需要几位同学出列。

输入输出样例:

示例: 1

输入

1
8 186 186 150 200 160 130 197 220

输出

1
4

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

答案解析：

要使得出列最少，那么就要留下最多的，我们想到了 $LIS$ ，但是 $LIS$ 只能处理单调序列最长，所以并不能直接用。

我们看到，这里是两头低，中间高的一种情况。

在这种情况下，最多的话那么就是最高的那个人的左侧加上右侧最高。

到这，我们发现。

在中间那个人左侧，从左到右做了一遍 $LIS$ 。

在那个人的右侧，从右到左的做了一遍 $LIS$ 。

至此，我们好像找了策略。

通过枚举中间那个人，然后看他左侧的 $LIS$ 和他右侧的$LIS$ 的值之和的大小，就能将这道题目解出。

C++ 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
#include <algorithm>
using namespace std;

int dp1[105],dp2[105],a[105],s[105];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        dp2[i]=1;
        dp1[i]=1;
    }//输入并赋初值

    //预处理，从右往左LIS
    for(int i=n-1;i>=1;i--)
    {
        for(int j=i+1;j<=n;j++)
        {
            if(a[i]>a[j]&&dp2[i]<=dp2[j]+1)
            {
                dp2[i]=dp2[j]+1;
            }
        }
    }
    //预处理，从左往右LIS
    for(int i=2;i<=n;i++)
    {
        for(int j=1;j<i;j++)
        {
            if(a[i]>a[j]&&dp1[i]<=dp1[j]+1)
            {
                dp1[i]=dp1[j]+1;
            }
        }
    }

    int maxx=0;
    for(int i=1;i<=n;i++)
    {
        s[i]=dp2[i]+dp1[i]-1;
        //自己算了两次，所以-1


        if(s[i]>maxx)
        {
            maxx=s[i];
        }
    }

    cout<<n-maxx;//是求出列的人数

}

Python 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
if __name__ == "__main__":

    # 输入并赋初值
    n = int(input().strip())

    t = list(map(int, input().split()))

    dp1 = [1] * n
    dp2 = [1] * n

    # 预处理，从左往右LIS
    for i in range(1, n):
        for j in range(i):
            if t[i] > t[j]:
                dp1[i] = max(dp1[i], dp1[j] + 1)

    # 预处理，从右往左LIS
    for i in range(n - 1, 0, -1):
        for j in range(n - 1, i, -1):
            if t[i] > t[j]:
                dp2[i] = max(dp2[i], dp2[j] + 1)


    maxx = 0

    for i in range(n):
        maxx = max(maxx, dp1[i] + dp2[i] - 1)
        # 自己算了两次，所以-1

    print(n - maxx)



Java 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {

        Scanner in = new Scanner(System.in);

        int n = in.nextInt();

        int[] a = new int[n];
        int[] dp1 = new int[n];
        int[] dp2 = new int[n];

        for (int i = 0; i < n; i++) {
            a[i] = in.nextInt();
            dp2[i]=1;
            dp1[i]=1;
        }//输入并赋初值


        //预处理，从左往右LIS
        for (int i = 0; i < n; i++) {

            for (int j = 0; j < i; j++) {
                if (a[i] > a[j] && dp1[j] + 1 > dp1[i]) {
                    dp1[i] = dp1[j] + 1;
                }
            }
        }

        //预处理，从右往左LIS
        for (int i = n - 1; i >= 0; i--) {

            for (int j = n - 1; j > i; j--) {
                if (a[i] > a[j] && dp2[j] + 1 > dp2[i]) {
                    dp2[i] = dp2[j] + 1;
                }
            }
        }

        int maxx = 0;

        for (int i = 0; i < n; i++) {
            maxx = Math.max(maxx, dp1[i] + dp2[i]-1);
            //自己算了两次，所以-1
        }

        // 是求出列的人数
        System.out.println(n - maxx );
    }
}

最优包含

题目链接：https://www.lanqiao.cn/problems/239/learning/

题目描述: 我们称一个字符串 $S$ 包含字符串 $T$ 是指 $T$ 是 $S$ 的一个子序列，即可以从字符串 $S$ 中抽出若干个字符，它们按原来的顺序组合成一个新的字符串与 $T$ 完全一样。

给定两个字符串 $S$ 和 $T$，请问最少修改 $S$ 中的多少个字符，能使 $S$ 包含 $T$ ？

其中，$1 \leq |T| \leq |S| \leq 1000$。

输入描述:

输入两行，每行一个字符串。

第一行的字符串为 $S$，第二行的字符串为 $T$。

两个字符串均非空而且只包含大写英文字母。

输出描述:

输出一个整数，表示答案。

输入输出样例:

示例:

输入

1
ABCDEABCD XAABZ

输出

1
3

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 256M

答案解析：

个题目是线性 DP 中比较经典的题目。

这个类型就做编辑距离，可以通过 DFS 解决，也可以通过 DP 解决。

DP 的时间复杂度低。

我们先来讲一下，编辑距离。

编辑距离为两个字符串，$a$ 和 $b$ 通过多少次变换，使得 $a$ 变成 $b$。

我们可以做出 $3$ 种操作。

$1.$ 删除操作，将 $a[i]$ 从 $a$ 中移除 $2.$ 插入操作，在 $a[i]$ 后加上 $b[j]$ $3.$ 替换操作，将 $a[i]$ 修改为 $b[j]$

编辑距离的状态转移类似 LCS ，但有有很大的差别。

初始状态，$i=j=0$，都在字符串的开头。

然后开始判断 $a[i]=?b[j]$

  • 如果相同，那么就不需要修改，所以$dp[i+1][j+1]=dp[i][j]$

    所以在$a[i-1]$等于$b[j-1]$时，$dp[i][j]$这个状态由$dp[i-1][j-1]$转移而来。

    $dp[i][j]=dp[i-1][j-1]$

  • 如果不同，那就需要进行三种可能的操作

  1. 修改操作：

    $a[i]$ 修改为 $b[j]$， 因为编辑了一次，所以$+1$

    $dp[i+1][j+1]=dp[i][j]+1$

    所以在$a[i-1]$不等于$b[j-1]$时，$dp[i][j]$这个状态由$dp[i-1][j-1]$转移而来。

    $dp[i][j]=dp[i-1][j-1]$

  2. 删除操作，直接把 $a[i]$ 删除，此时转移到 $dp[i][j+1]$ ，因为 $a[i]$ 被删除，但是下一个字符到了 $a[i]$ 的位置，而对应比较的位置到了$b[j+1]$。

    所以此时状态转移到了$dp[i][j+1]$

    $dp[i][j+1]=dp[i][j]+1$

    因为编辑了一次，所以$+1$

    所以在$a[i-1]$不等于$b[j-1]$时，$dp[i][j]$就有可能通过$dp[i-1][j]$转移而来。

  3. 插入操作，在$a[i]$后添加一个$b[j]$，那么此时$a[i+1]$和$b[j]$对应，因为加了一个字符就变成了$a[i+1]$,而且跟$b[j]$对应，那么下一个状态转移到了$dp[i+1][j]$

    $dp[i+1][j]=dp[i][j]+1$

    此时状态转移到了 $dp[i+1][j]=dp[i][j]+1$

    因为编辑了一次，所以$+1$

    所以在$a[i-1]$不等于$b[j-1]$时，$dp[i][j]$就有可能通过$dp[i][j-1]$转移而来。

那么不同时，我们选择他们的最小值即可。

由此我们可以写出模板：

C++ 解题代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<algorithm>
#include<set>
#include<string>

using namespace std;
#define INF 99999999
string s, t;
int dp[1010][1010];

void init(){
    for (int i = 0; i <= s.size(); i++) dp[i][0] = 0;
    for (int j = 1; j <= t.size(); j++) dp[0][j] = INF;
}

int main() {
    cin >> s >> t;

    init();

    for (int i = 1; i <= s.size(); i++) {
        for (int j = 1; j <= t.size(); j++) {
            if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1];
            else
                dp[i][j] = min(dp[i - 1][j - 1],min(dp[i - 1][j], dp[i][j - 1])) + 1;
        }
    }
    cout << dp[s.size()][t.size()];
    return 0;
}

Python 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


def init(s,t):

    dp = [[0 for i in range(len(t) + 1)] for j in range(len(s) + 1)]
    for i in range(len(s) + 1):
        dp[i][0] = 0

    for j in range(1,len(t) + 1):
        dp[0][j] = 999999

    return dp

if __name__ == '__main__':
    s = list(input())
    t = list(input())

    dp=init(s,t)

    for i in range(len(s)):
        for j in range(len(t)):
            if s[i] == t[j]:
                dp[i + 1][j + 1] = dp[i][j]
            else:
                dp[i + 1][j + 1] = min(dp[i][j] + 1, dp[i][j + 1])
                dp[i + 1][j + 1] = min( dp[i + 1][j + 1] ,dp[j+1][i]+1)

    print(dp[-1][-1])

Java 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import java.util.Scanner;

public class Main {
    public static   int dp[][];

    public static void init(int n,int m){

        dp = new int[n+1][m+1];
        for (int i = 0; i <= n; i++) dp[i][0] = 0;
        for (int j = 1; j <= m; j++) dp[0][j] = 99999;
    }

    public static void main(String[] args) {

        Scanner in = new Scanner(System.in);

        String s = in.nextLine();
        String t = in.nextLine();

        int n = s.length();
        int m = t.length();

        init(n,m);

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1];
                else  dp[i][j] = min(dp[i - 1][j - 1],min(dp[i - 1][j], dp[i][j - 1])) + 1;
            }
        }

        System.out.println(dp[n][m]);

    }
}

这道题目也比较简单，由于是包含关系，并不是相等关系，所以当 S 多余 T 是，不需要进行删除操作。

所以这个题目不考虑删除的那个状态转移即可。

C++ 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<algorithm>
#include<set>
#include<string>

using namespace std;
#define INF 99999999
string s, t;
int dp[1010][1010];

void init(){
    for (int i = 0; i <= s.size(); i++) dp[i][0] = 0;
    for (int j = 1; j <= t.size(); j++) dp[0][j] = INF;
}

int main() {
    cin >> s >> t;

    init();

    for (int i = 1; i <= s.size(); i++) {
        for (int j = 1; j <= t.size(); j++) {
            if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1];
            else dp[i][j] = min(dp[i - 1][j - 1] + 1, dp[i - 1][j]);

        }
    }
    cout << dp[s.size()][t.size()];
    return 0;
}

Python 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def init(s,t):

    dp = [[0 for i in range(len(t) + 1)] for j in range(len(s) + 1)]
    for i in range(len(s) + 1):
        dp[i][0] = 0

    for j in range(1,len(t) + 1):
        dp[0][j] = 999999

    return dp

if __name__ == '__main__':
    s = list(input())
    t = list(input())

    dp=init(s,t)

    for i in range(len(s)):
        for j in range(len(t)):
            if s[i] == t[j]:
                dp[i + 1][j + 1] = dp[i][j]
            else:
                dp[i + 1][j + 1] = min(dp[i][j] + 1, dp[i][j + 1])

    print(dp[-1][-1])

Java 解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import java.util.Scanner;

public class Main {
    public static   int dp[][];

    public static void init(int n,int m){

        dp = new int[n+1][m+1];
        for (int i = 0; i <= n; i++) dp[i][0] = 0;
        for (int j = 1; j <= m; j++) dp[0][j] = 99999;
    }

    public static void main(String[] args) {

        Scanner in = new Scanner(System.in);

        String s = in.nextLine();
        String t = in.nextLine();

        int n = s.length();
        int m = t.length();

        init(n,m);

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1];
                else dp[i][j] = Math.min(dp[i - 1][j - 1] + 1, dp[i - 1][j]);

            }
        }

        System.out.println(dp[n][m]);

    }
}

实验总结

动态规划的学习是痛苦的，也是快乐，而且是非常重要的。

希望大家努力克服，动态规划都学会了还有什么学不会呢。

≡