组合数学

First Post:

2024-03-11

Last Update:

2024-03-31

组合数学

计数原理：加法原理

加法原理：集合 $S$ 被分成两两不相交的部分 $S_1, S_2, S_3, …, S_m$，那么 $S$ 的对象数目等于：$|S| = |S_1| + |S_2| + |S_3| + … + |S_m|$
例：一个学生想学一门数学课，一门文化课，但不能同时选，现在从 $4$ 门数学课和 $4$ 门文化课中选，一共有 $4 + 4 = 8$ 种方法选一门课。
加法原理的关键是将计数分解为若干个独立（不相容）的部分，保证既不重复也不遗漏地进行计数。加法原理是利用完备事件组的一个体现，我们可以利用一个集合的补记做题。

例题：分割立方体 lanqiaoOJ 题号 1620

题目描述： 一个立方体，边长为 $n$，分割成 $n × n × n$ 个单位立方体。任意两个单位立方体，或者有 $2$ 个公共点，或者有 $4$ 个公共点，或者没有公共点。请问，没有公共点和有 $2$ 个公共点的立方体，共有多少对？

输入描述： 一个整数 $n，1 \leq n \leq 30$

思路： 反过来计算，先算出有 $4$ 个公共点的立方体有多少对，然后用总对数减去。分几种情况讨论：

正方体和周围 $3$ 个正方体相邻，这种情况共有 $8$ 个，就是顶角上的 $8$ 个，总个数 $3 \times 8$；
正方体和周围 $4$ 个正方体相邻，这种情况共有 $(n-2) \times 12$ 个（棱）总个数 $4 \times (n-2) \times 12$；
正方体和周围 $5$ 个正方体相邻，这种情况共有 $6 \times (n \times n - 4 \times n + 4)$ 个，总个数 $5 \times 6 \times (n \times n - 4 \times n + 4)$；
正方体和周围 $6$ 个正方体相邻，这种情况共有 $(n \times n \times n - n \times n \times 6 + n \times 12 - 8)$ 个，总个数 $6 \times (n \times n \times n - n \times n \times 6 + n \times 12 - 8)$；最后把这 $4$ 个情况求和再除以 $2$。

正方体一共 $n^3$ 个，共有 $\frac{n^3(n^3 - 1)}{2}$ 种关系

正方体和周围 $3$ 个正方体相邻，总个数 $3 \times 8$；
正方体和周围 $4$ 个正方体相邻，总个数 $4 \times (n-2) \times 12$；
正方体和周围 $5$ 个正方体相邻，总个数 $5 \times 6 \times (n \times n - 4 \times n + 4)$；
正方体和周围 $6$ 个正方体相邻，总个数 $6 \times (n \times n \times n - n \times n \times 6 + n \times 12 - 8)$；
最后把这 $4$ 个情况求和再除以 $2$。

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n; cin >> n;
    if(n == 1){             // 边长为 1 时特判
        cout << 0 << endl;
        return 0;
    }
    long long sum = n * n * n * (n * n * n - 1) / 2;     //总数
    int edge3 = 8;
    int ans3 = 3 * edge3;
    int edge4 = (n - 2) * 12;
    int ans4 = 4 * edge4;
    int edge5 = n * n - 4 * n + 4;
    int ans5 = 5 * 6 * edge5;
    int edge6 = n * n * n - n * n * 6 + n * 12 - 8;
    int ans6 = 6 * edge6;
    cout << sum - (ans3 + ans4 + ans5 + ans6) / 2 << endl;
    return 0;
}

n = int(input())
if n == 1: # 边长为 1 时特判
    print(0)
else:
    sum = n * n * n * (n * n * n - 1) // 2 # 总数
    edge3 = 8
    ans3 = 3 * edge3
    edge4 = (n - 2) * 12
    ans4 = 4 * edge4
    edge5 = n * n - 4 * n + 4
    ans5 = 5 * 6 * edge5
    edge6 = n * n * n - n * n * 6 + n * 12 - 8
    ans6 = 6 * edge6
    print(sum - (ans3 + ans4 + ans5 + ans6) // 2)

import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        if (n == 1) { // 边长为 1 时特判
            System.out.println(0);
            return;
        }
        long sum = (long) n * n * n * (n * n * n - 1) / 2; // 总数
        int edge3 = 8;
        int ans3 = 3 * edge3;
        int edge4 = (n - 2) * 12;
        int ans4 = 4 * edge4;
        int edge5 = n * n - 4 * n + 4;
        int ans5 = 5 * 6 * edge5;
        int edge6 = n * n * n - n * n * 6 + n * 12 - 8;
        int ans6 = 6 * edge6;
        System.out.println(sum - (ans3 + ans4 + ans5 + ans6) / 2);
    }
}

计数原理：乘法原理

令 $S$ 是对象的有序对 $(a, b)$ 的集合，其中第一个对象 $a$ 来自大小为 $p$ 的一个集合，对于对象 $a$ 的每个选择，对象 $b$ 有 $q$ 个选择，那么 $S$ 的大小：$|S| = p \times q$

例：中性笔的长度有 $3$ 种，颜色有 $4$ 种，直径有 $5$ 种。不同种类的中性笔有：$3 \times 4 \times 5 = 60$ 种。

例：$34 \times 55 \times 72 \times 113$ 的正整数因子有多少？答：这是算数基本定理的概念。$3$ 有 $0$ ~ $4$ 这 $5$ 种选择，$5$ 有 $6$ 个选择，$7$ 有 $3$ 个选择，$11$ 有 $4$ 个选择，因子总数是 $5 \times 6 \times 3 \times 4 = 360$ 种。

排列数

排列是有序的。

不可重复排列数：从 $n$ 个不同的物品中取出 $r$ 个，排列数为：

$\mathrm{A_{n}^{r}=n(n-1)(n-2)…(n-r+1)=\frac{n!}{(n-r)!}}$

可重复排列数，从 $n$ 个不同的物品中可重复地取出 $r$ 个的排列数为：$n^r$。

组合数

排列是有序的，组合是无序的。

如果 $S$ 中的元素都不相同，组合数：

$\mathrm{C_{n}^{r}={\binom{n}{r}}={\frac{A_{n}^{r}}{r!}}={\frac{n!}{r!(n-r)!}}}$

糊涂人寄信 lanqiaoOJ 题号 1622

题目描述： 有一个糊涂人，写了 $n$ 封信和 $n$ 个信封，到了邮寄的时候，把所有的信都装错了信封。求装错信封可能的种类数。

输入描述： 每行输入一个正整数 $n$，表示一种情况。$(n \leq 20)$

输出描述： 输出相应的答案。

解题思路：

题目建模为：有 $1 \sim n$ 个数字，分别放在 $n$ 个位置，问都放错的情况有多少种。

用 DP 来做。定义 $dp[]$，$dp[i]$ 表示数字 $1 \sim i$ 都放错的种类数。$dp[n]$ 是答案。

下面考虑状态转移方程，从 $1 \sim i$ 递推到 $i$。

数字 $i$ 如果放错，有 $i-1$ 个位置可以放，假设其放在第 $k$ 个位置。对于数字 $k$，可以放在 $i$ 位置也可以不放在 $i$ 位置。

如果 $k$ 放在 $i$ 位置，那么对于剩下 $i-2$ 个数字放的次数，就是 $i-2$ 个数字都放错的方法数 $dp[i-2]$。

如果 $k$ 不放在 $i$ 位置，和 $i-1$ 个数字放错的情况相同，为 $dp[i-1]$。

状态转移方程：$dp[i] = (i-1) \times (dp[i-1] + dp[i-2])$

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[30];
int main(){
    dp[1]= dp[0]=0;
    dp[2]=1;
    for(int i=3;i<=22;i++) dp[i]=(i-1)*(dp[i-1]+dp[i-2]);
    int n;
    while(cin>>n) cout<<dp[n]<<endl;
    return 0;
}

import sys
def f(n):
    if n==0 or n==1: return 0
    elif n==2:  return 1
    else:  return (n-1)*(f(n-1)+f(n-2))
for n in sys.stdin:   #读入n，和C++代码的while(cin>>n)功能一样
    n = int(n)
    print(f(n))

import java.util.Scanner;

public class Main {
    static long[] dp = new long[30];
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        dp[1] = dp[0] = 0;
        dp[2] = 1;
        for (int i = 3; i <= 22; i++) {
            dp[i] = (i - 1) * (dp[i - 1] + dp[i - 2]);
        }
        while (sc.hasNext()) {
            int n = sc.nextInt();
            System.out.println(dp[n]);
        }
        sc.close();
    }
}

鸽巢原理

鸽巢原理，又称抽屉原理。

鸽巢原理： 把 $n+1$ 个物体放进 $n$ 个盒子，至少有一个盒子包含 $2$ 个或更多的物体。

例：在 $370$ 人中，至少有 $2$ 人生日相同；
例：$n$ 个人互相握手，一定有 $2$ 个人握手次数相同。

例：$n$ 个人互相握手，一定有 $2$ 个人握手次数相同。每人跟其他人握手，最少可以是 $0$ 次，最多可以是$n-1$次。如果握手最少的是 $0$ 次，那么剩下的$n-1$人中，握手最多的人不会超过$n-2$次。$0 \sim n-2$ 共$n-1$种情况。如果握手最少的张三是 $1$ 次，那么剩下的$n-1$人中，握手最多的李四除了跟张三握手一次，跟其他$n-2$人最多握手$n-2$次，李四最多握手$n-1$次。$1 \sim n-1$ 共$n-1$种情况。如果握手最少的张三是 $2$ 次，那么剩下的$n-1$人中，握手最多的李四除了跟张三握手一次，跟其他$n-2$人最多握手$n-2$次，李四最多握手$n-1$次。$2 \sim n-1$ 共$n-2$种情况。 …… 所以握手次数最多有$n-1$种情况，最少只有 $1$ 种情况。把最多的$n-1$种情况看成$n-1$个抽屉，$n$个人放进这$n-1$个抽屉，至少有一个抽屉里面有 $2$ 人。

例题：小蓝吃糖果 lanqiaoOJ 题号 1624

题目描述： Gardon 有 $n$ 种糖果，每种数量已知。Gardon 不喜欢连续 $2$ 次吃同样的糖果。问有没有可行的吃糖方案。

输入： 第一行是整数 N，$0 < n < 1000000$，第二行是 $n$ 个数，表示 $n$ 种糖果的数量 $m_i$，$0 < m_i < 1000000$

输出： 输出一行，包含一个 “Yes” 或 “no”。

解题思路

继续处理格式，鸽巢原理，用“隔板法”求解。

找出最多的一种糖果，把它的数量 $K$ 看成 $K$ 个隔板，隔成 $K$ 个空间（把每个隔板的右边看成一个空间）；其它所有糖果的数量为 $S$。

最多的一种糖果，把它的数量 $K$ 看成 $K$ 个隔板，隔成 $K$ 个空间（把每个隔板的右边看成一个空间）；其它所有糖果的数量为 $S$。

（1）如果 $S < K-1$，把 $S$ 个糖果放到隔板之间，这 $K$ 个隔板不够放，必然至少有 2 个隔板之间没有糖果，由于这 2 个隔板是同一种糖果，所以无解。
（2）$S \geq K-1$ 时，肯定有解。其中一个解是：把 $S$ 个糖果排成一个长队，其中同种类的糖果是挨在一起的，然后每次取 $K$ 个糖果，按顺序一个一个地放进 $K$ 个空间。由于隔板数量比每一种糖果的数量都多，所以不可能有 $2$ 个同样的糖果被放进一个空间里。把 $S$ 个糖果放完，就是一个解，一些隔板里面可能放好几种糖果。

#include<bits/stdc++.h>
using namespace std;
int a[1005000];
int main(){
    long long sum=0;
    int Max=0;
    int n; scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        sum += a[i];              //所有糖果数量
        if(a[i]>Max)  Max=a[i];   //最多的一种糖果
    }
    if(sum-Max+1>=Max) printf("Yes\n");
    else               printf("No\n");
return 0;
}

n=int(input())
a=list(map(int,input().split()))
if sum(a)-max(a) < max(a)-1:
    print("No")
else:
    print("Yes")

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        long sum = 0;
        int max = 0;
        int n = input.nextInt();
        for (int i = 1; i <= n; i++) {
            int x = input.nextInt();
            sum += x;
            if (x > max) {
                max = x;
            }
        }
        if (sum - max + 1 >= max) {
            System.out.println("Yes");
        } else {
            System.out.println("No");
        }
    }
}

二项式定理和杨辉三角

杨辉三角：排列成如下三角形的数字

      1
    1   1
   1  2  1
 1   3  3  1
1  4   6  4  1

每个数是它上面 $2$ 个数的和。

求杨辉三角第 $n$ 行的数字，可以模拟这个推导过程，逐级递推，复杂度 $O(n^2)$。

用数学公式计算，可以直接得到结果，这个公式是$(1 + x)n$。

图片描述

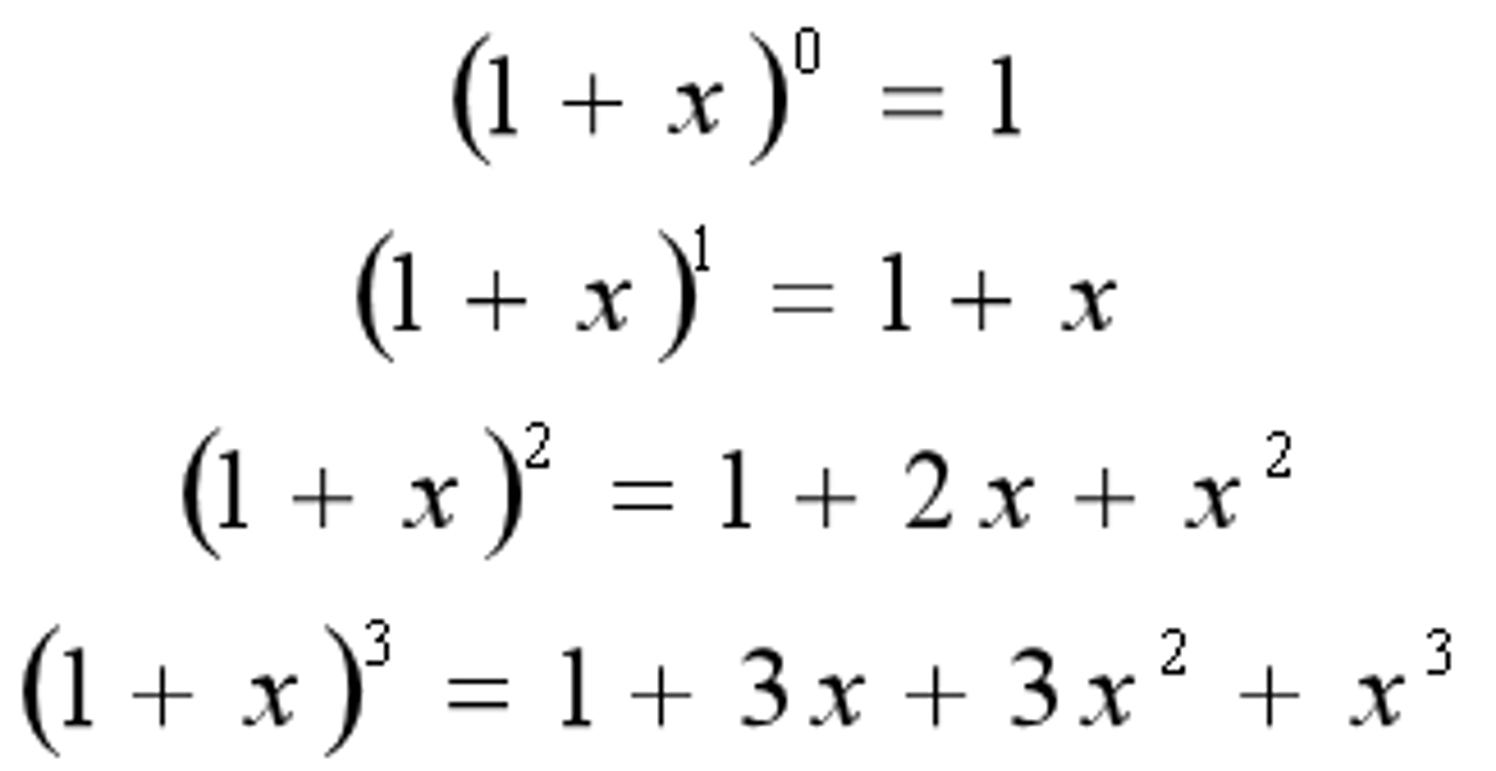
二项式系数就是$(1 + x)^n$ 展开后第 $r$ 项的系数。

$\mathrm{C_{n}^{r}={\binom{n}{r}}=\frac{n!}{r!(n-r)!}}$

对应杨辉三角的第 $n$ 行第 $r$ 个数是

例：杨辉三角的第 $4$ 行是“$1 3 3 1$”，

$\mathrm{C_{n-1}^{r-1}=C_{4-1}^{1-1}=C_3^0=1、C_3^1=3、C_3^2=3、C_3^3=1}$

理解：$(1 + x)^n$ 的第 $r$ 项，就是从 $n$ 个 $x$ 中选出 $r$ 个，这就是组合数的定义

当 n 较大，且需要取模时，二项式系数有两种计算方法：

（1）递推公式：$\mathrm{C_{n}^{r}=C_{n-1}^{r}+C_{n-1}^{r-1}}$

公式是杨辉三角的定义，即“每个数是它上面 $2$ 个数的和”。计算复杂度是 $O(n^2)$。

（2）用逆直接计算

因为输出取模，那么不用递推公式，直接用公式计算更快。不过，由于除法不能直接取模，需要用到逆。用逆计算二项式系数，有：

$\mathrm{C_{n}^{r}={\binom{n}{r}}=\frac{n!}{r!(n-r)!}}$

$\mathrm{C_{r}^{n}\bmod m=\frac{n!}{r!(n-r)!}\bmod m=(n!\bmod m)((r!)^{-1}\bmod m)(((n-r)!)^{-1}\bmod m)\bmod m}$

用逆计算二项式系数，复杂度是 $O(n)$ 的。

≡