【蓝桥杯】国赛知识梳理
动态规划
基础
线性DP



动态规划分析步骤

模板题——破损的楼梯
1 | |
1 | |
二维DP

分析步骤

模板题——数字三角形
1 | |


模板题——摆花
1 | |
模板题——选数异或
1 | |
LIS
最长上升子序列


模板题——蓝桥勇士
1 | |
模板题——合唱队形
1 | |
LCS
最长公共子序列

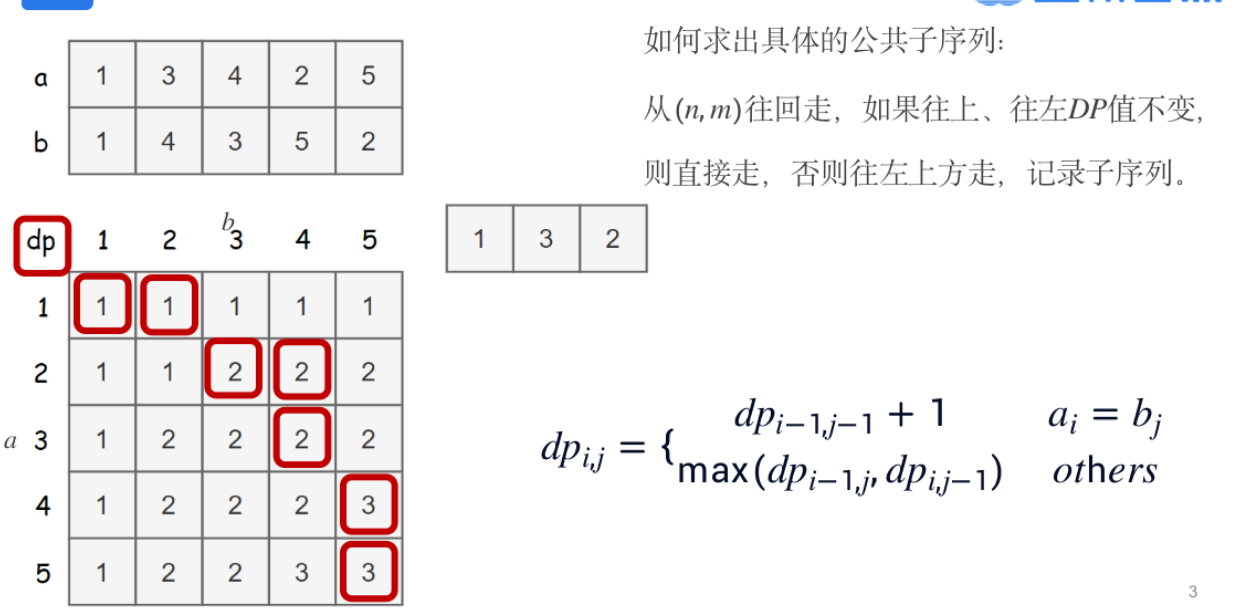
模板题——最长公共子序列
1 | |

背包DP
01背包



模板题——小明的背包1
1 | |
滚动数组优化



1 | |
完全背包




模板题——小明的背包2

1 | |
滚动数组优化
1 | |
多重背包


模板题——小明的背包3



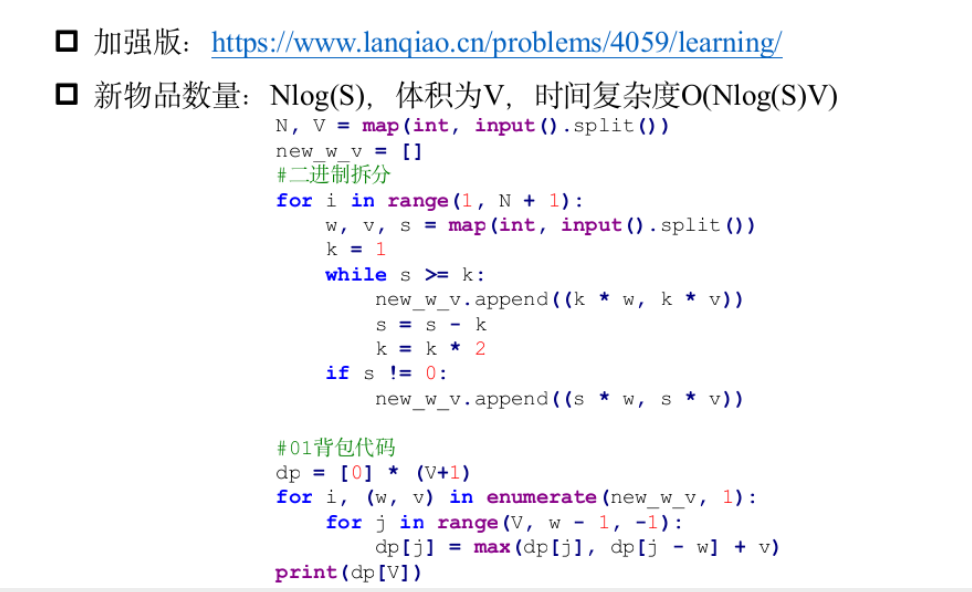
1 | |
滚动数组优化
1 | |
二维费用背包&分组背包


模板题——小蓝的神秘行囊
1 | |
1 | |
树形DP
自上而下树形DP
1 | |
自下而上树形DP
1 | |
路径相关树形DP
1 | |
换根DP
1 | |
区间DP


普通区间DP
模板题——石子合并
1 | |
模板题——涂色
1 | |
模板题——制作回文串
1 | |
环形区间DP
模板题——能量项链
1 | |
状压DP


模板题——例1

1 | |
模板题——例2

1 | |
数位DP
期望DP
数据结构
链表,栈,队列
链表
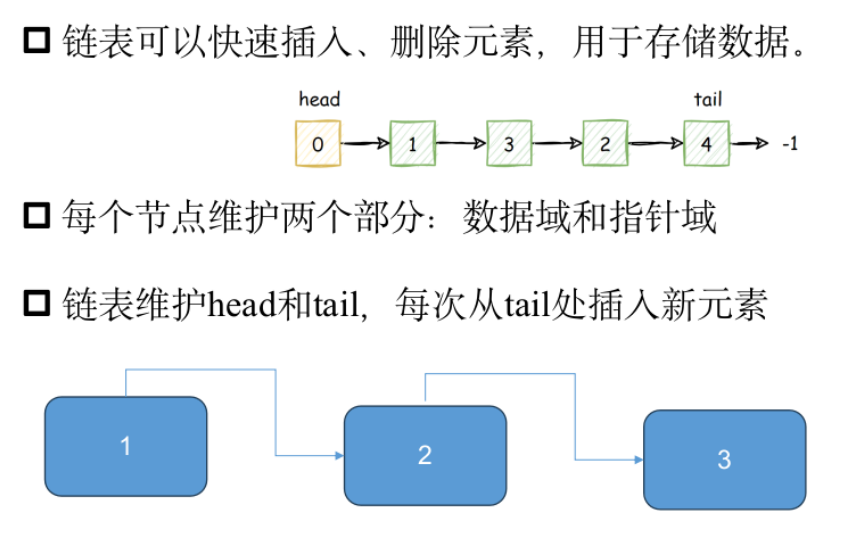
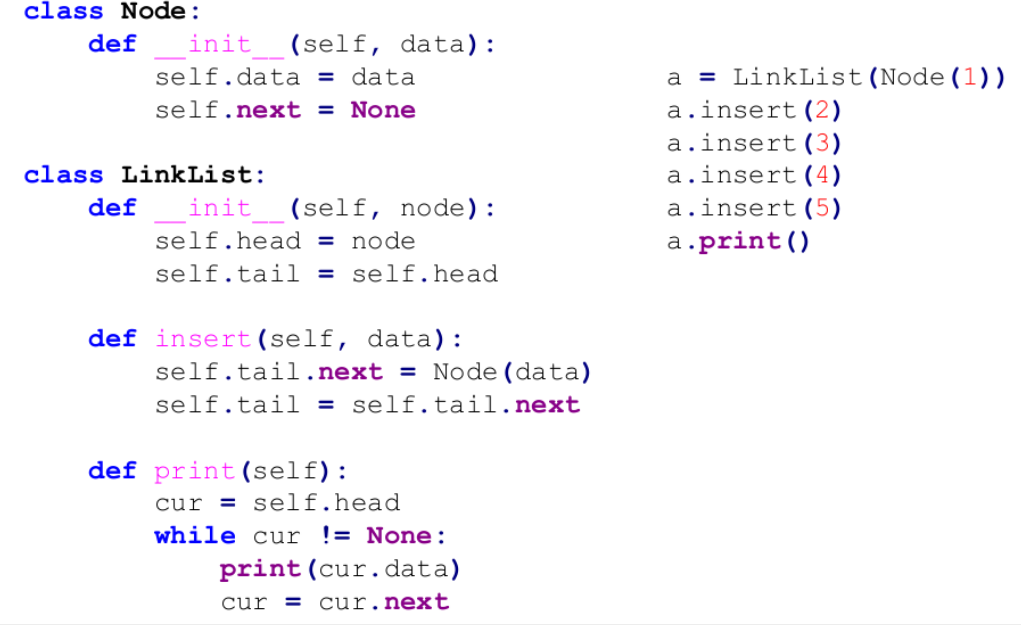

模板题——约瑟夫环
1 | |
栈
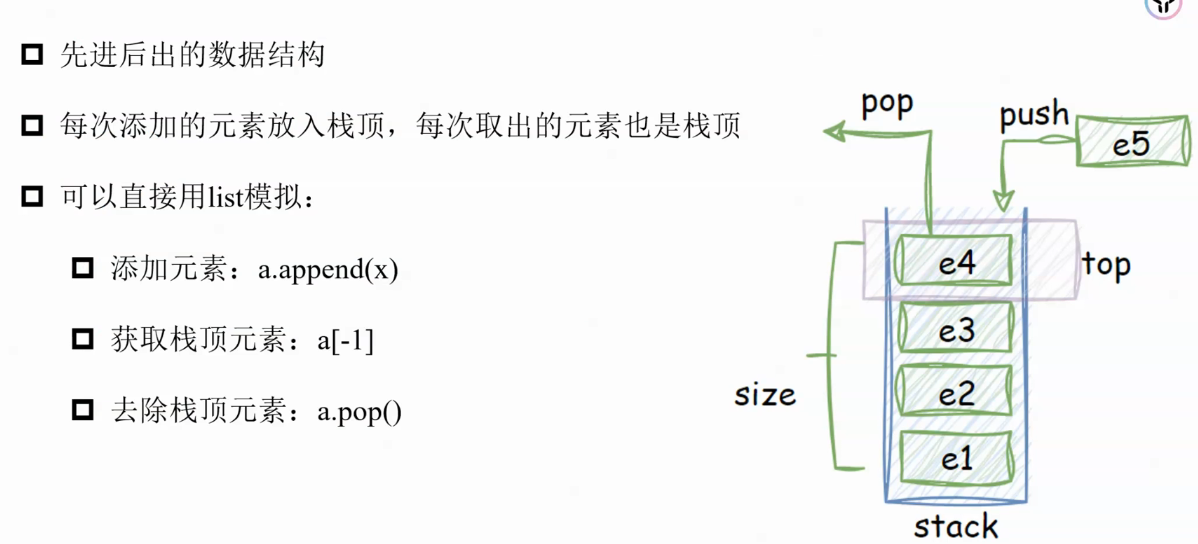
模板题——小蓝的括号串1
1 | |
队列

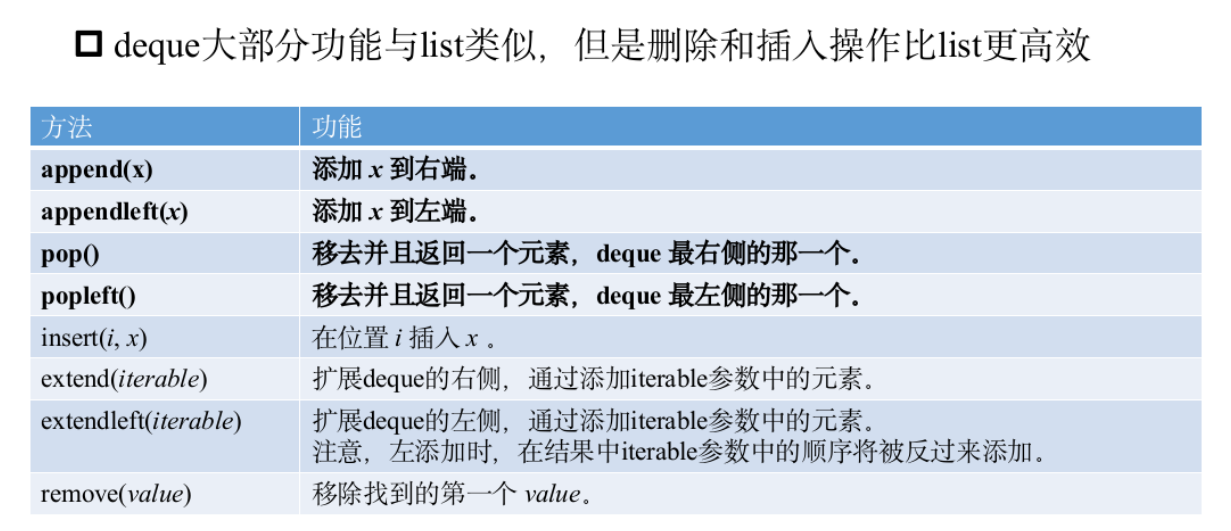

模板题——队列操作
1 | |
堆
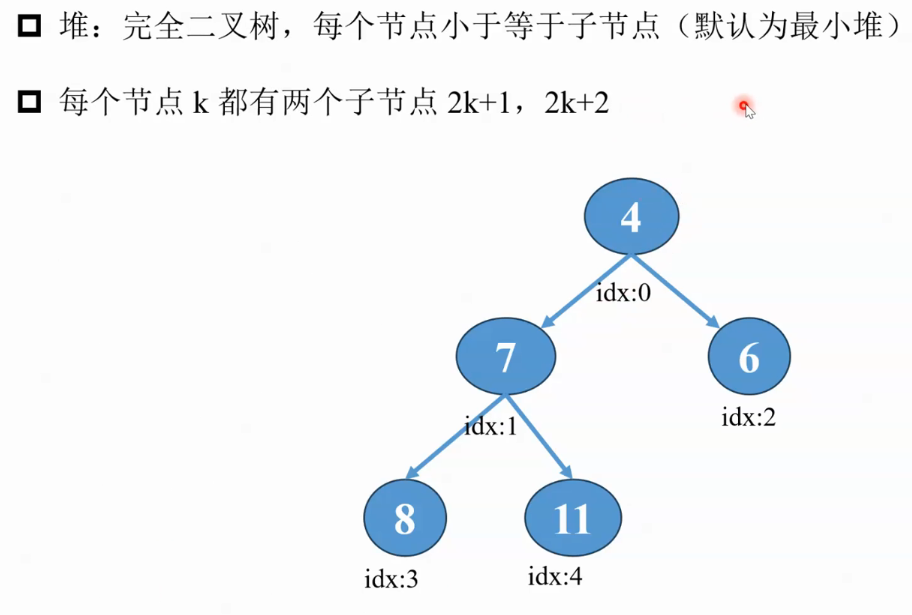

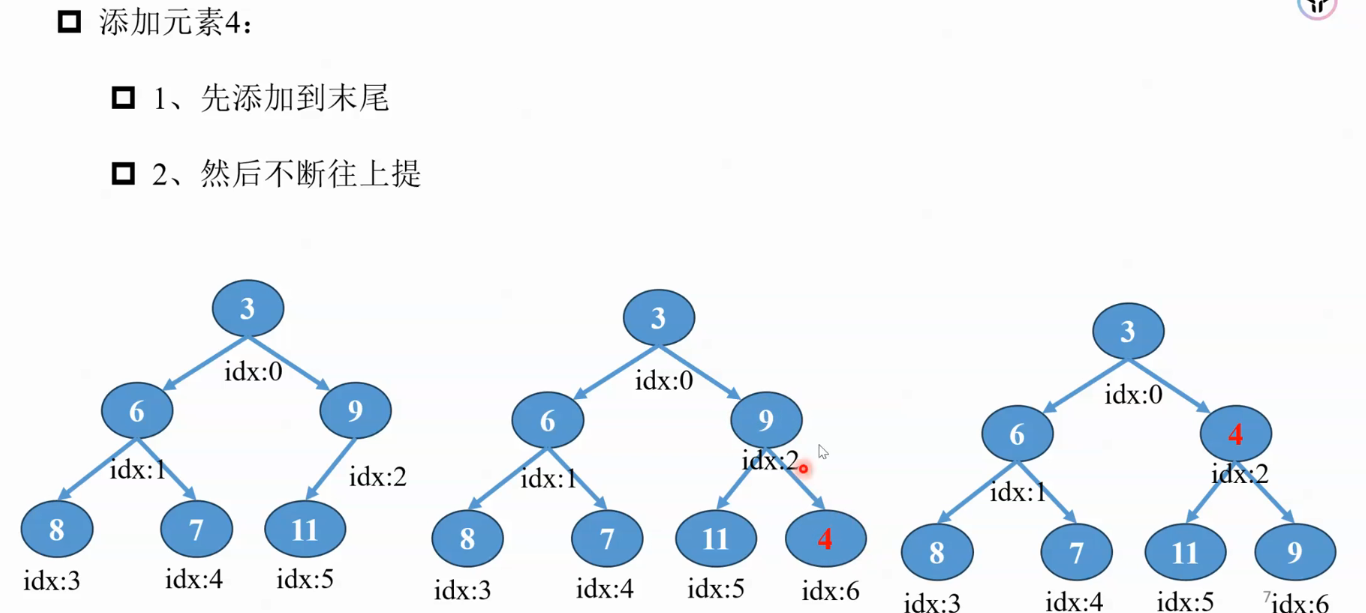
优先队列



模板题——小蓝的神奇复印机
1 | |
ST表
RMQ问题



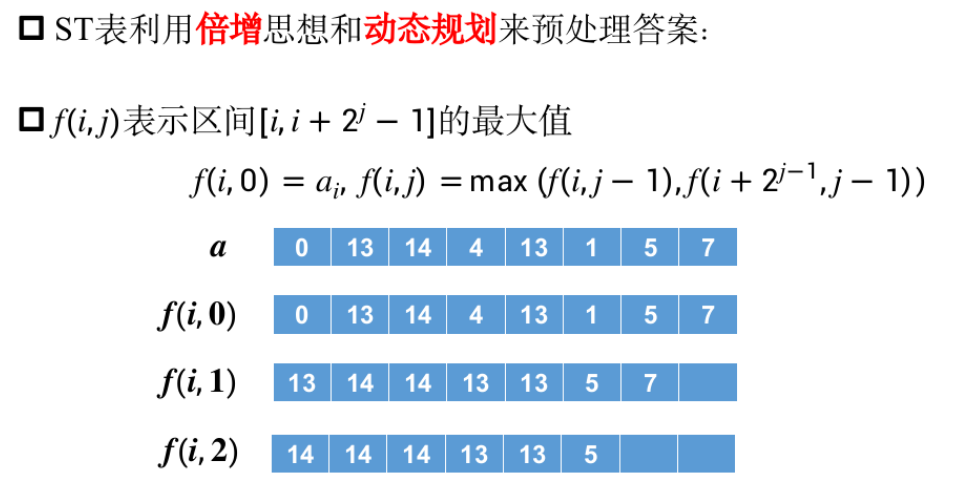

并查集
基础并查集
基础

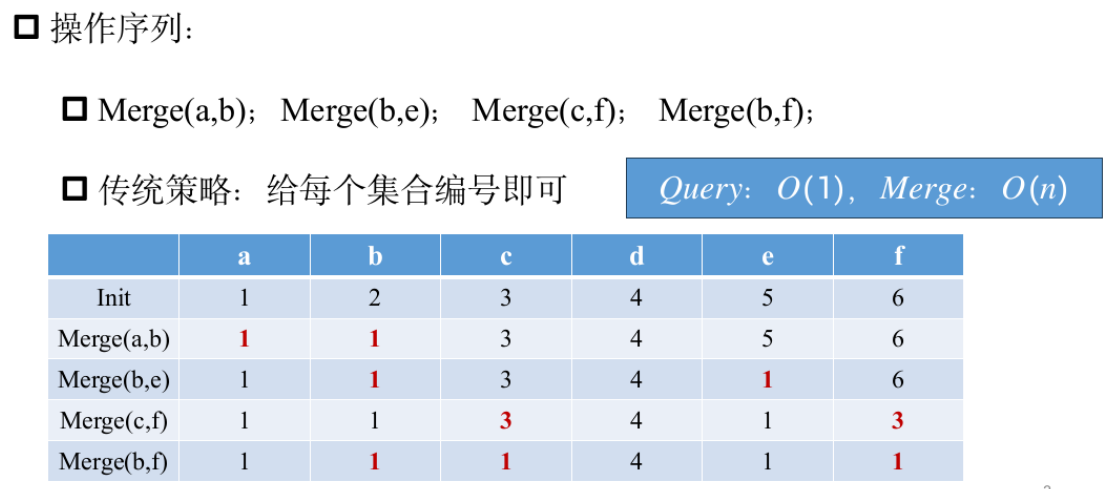
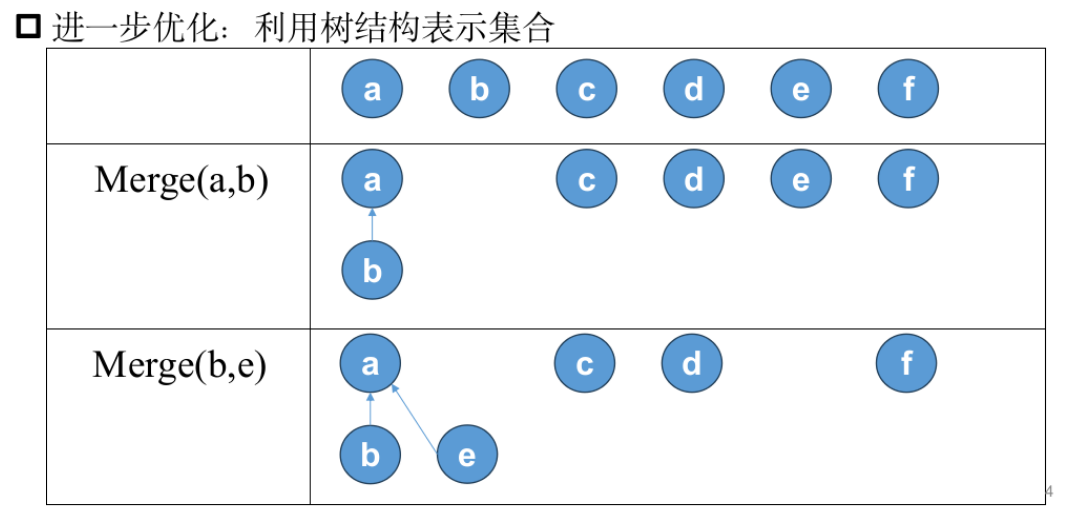
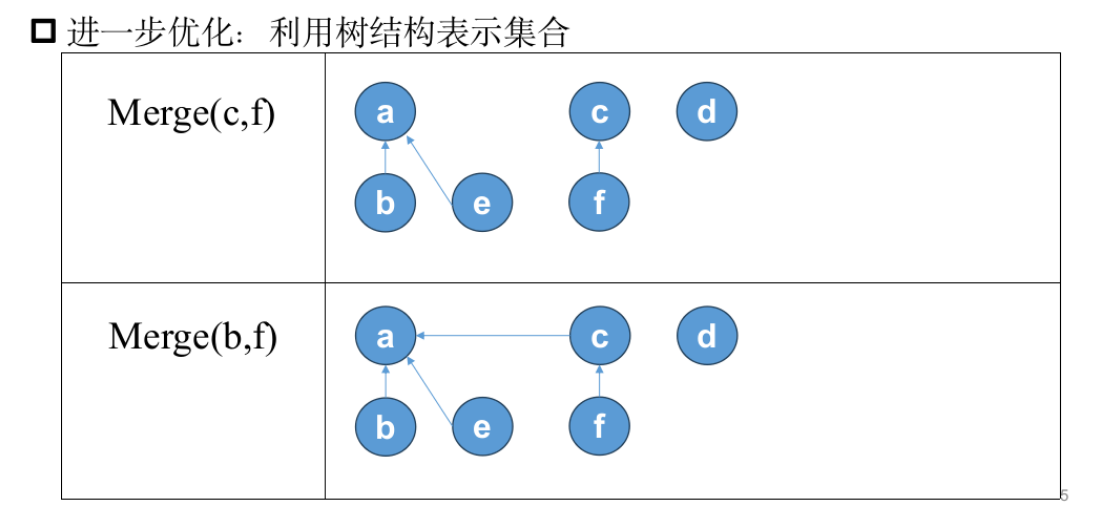

模板题——蓝桥幼儿园
1 | |
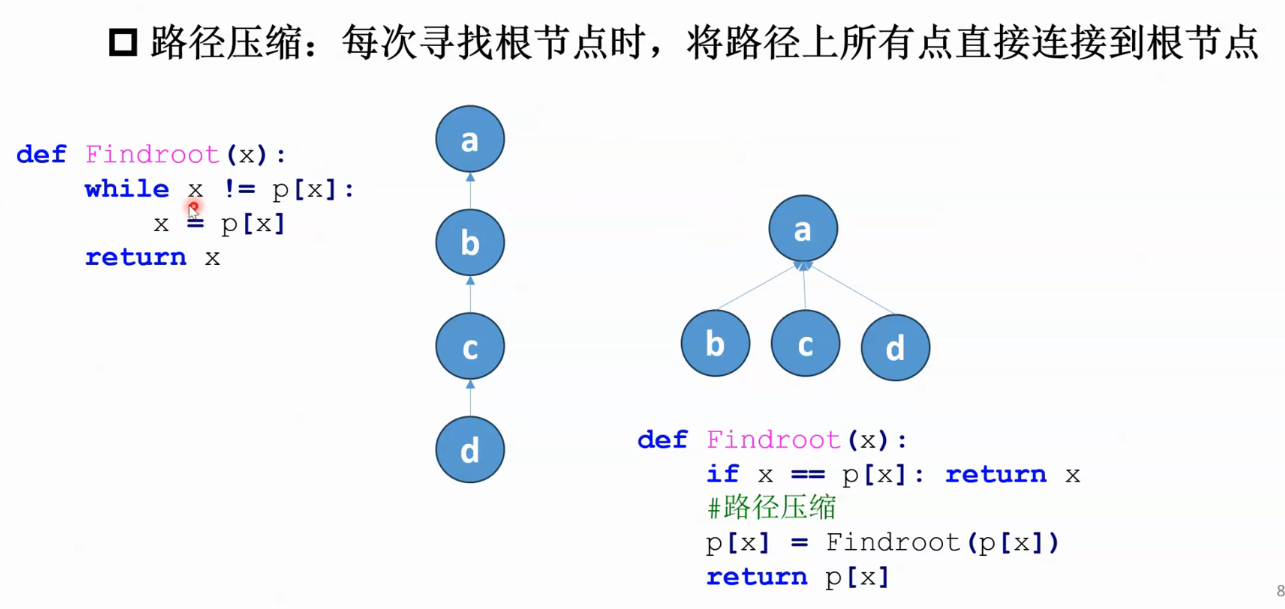
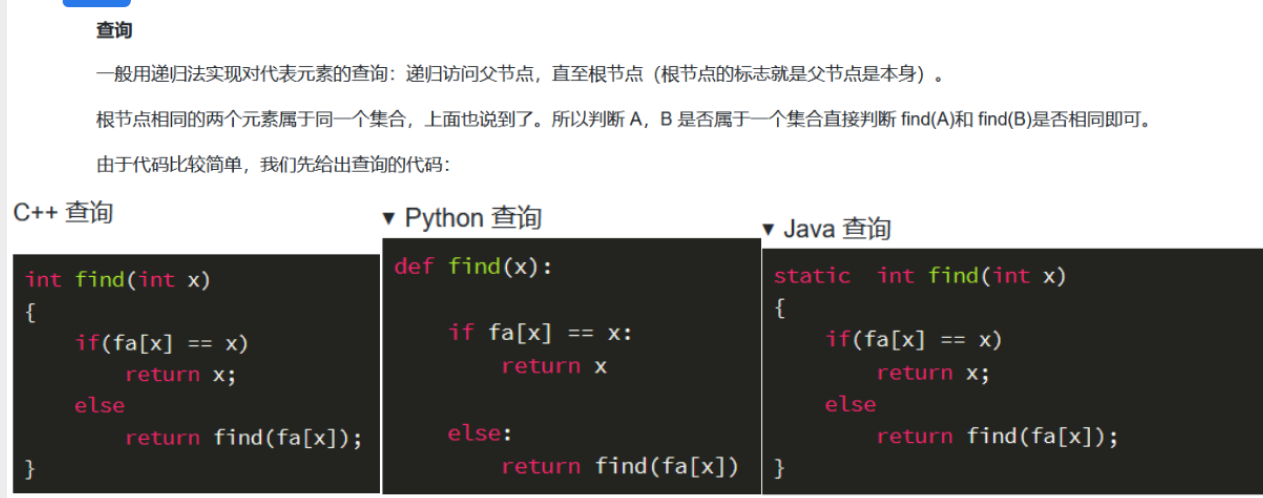
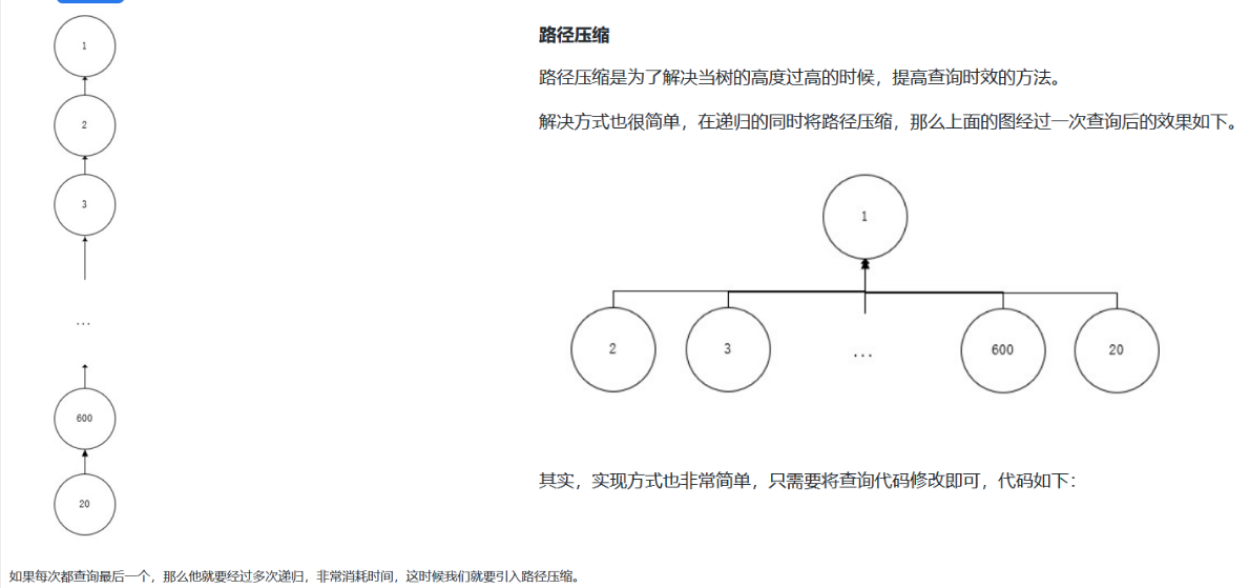
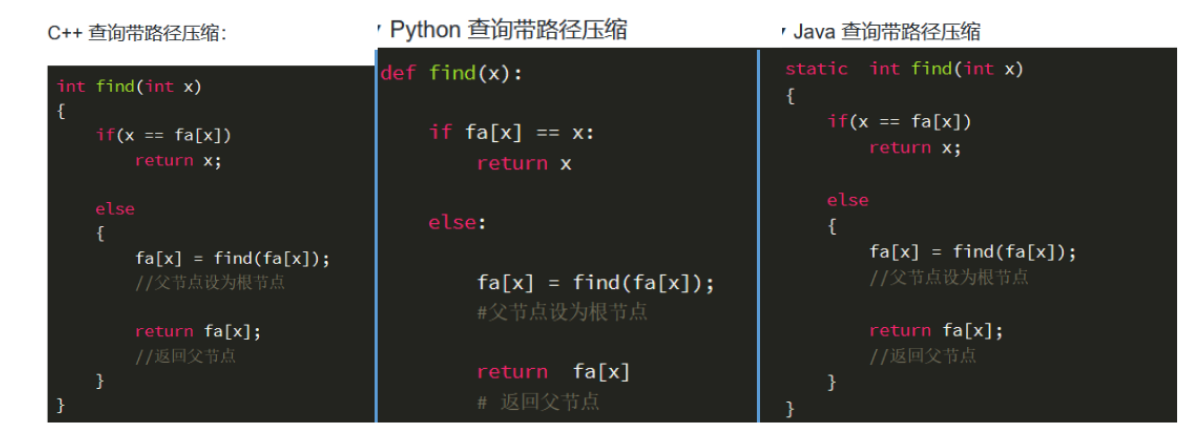
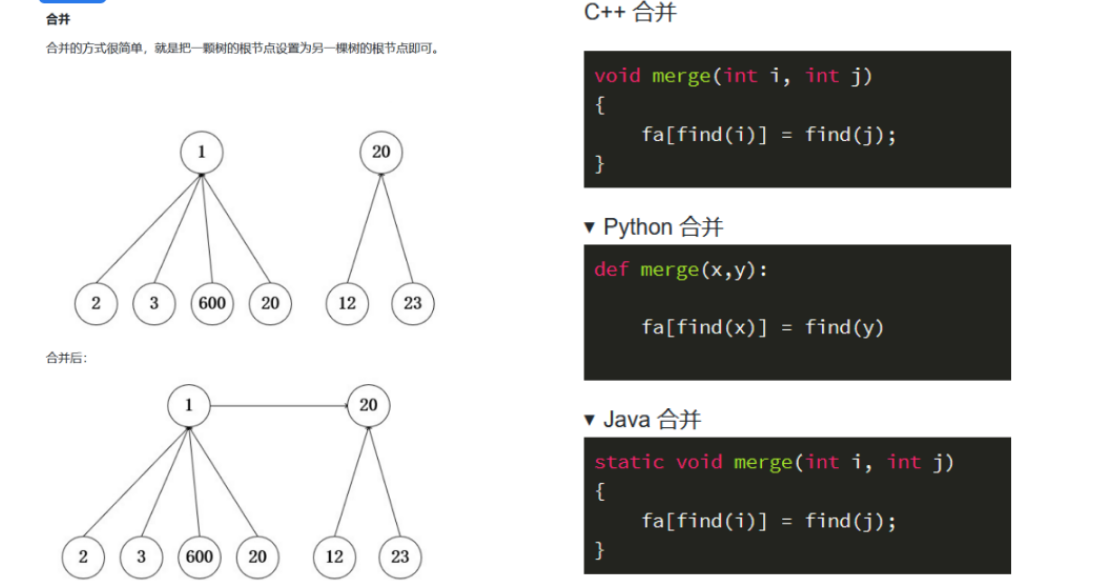
路径压缩
模板题——星球大战
1 | |
可撤销并查集



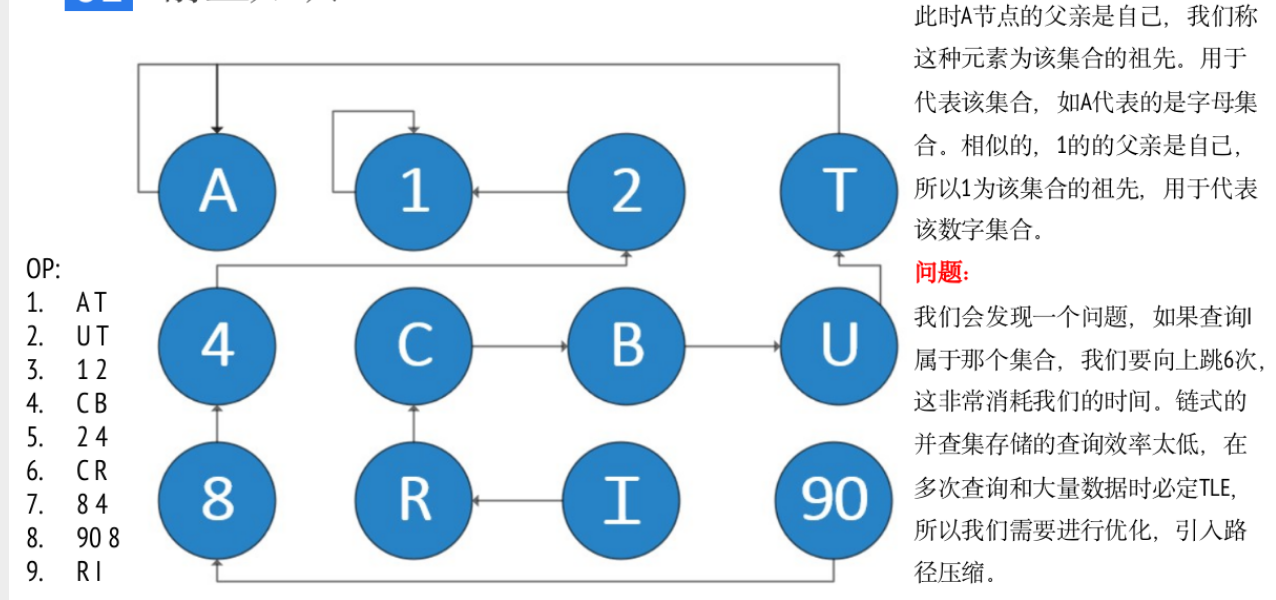
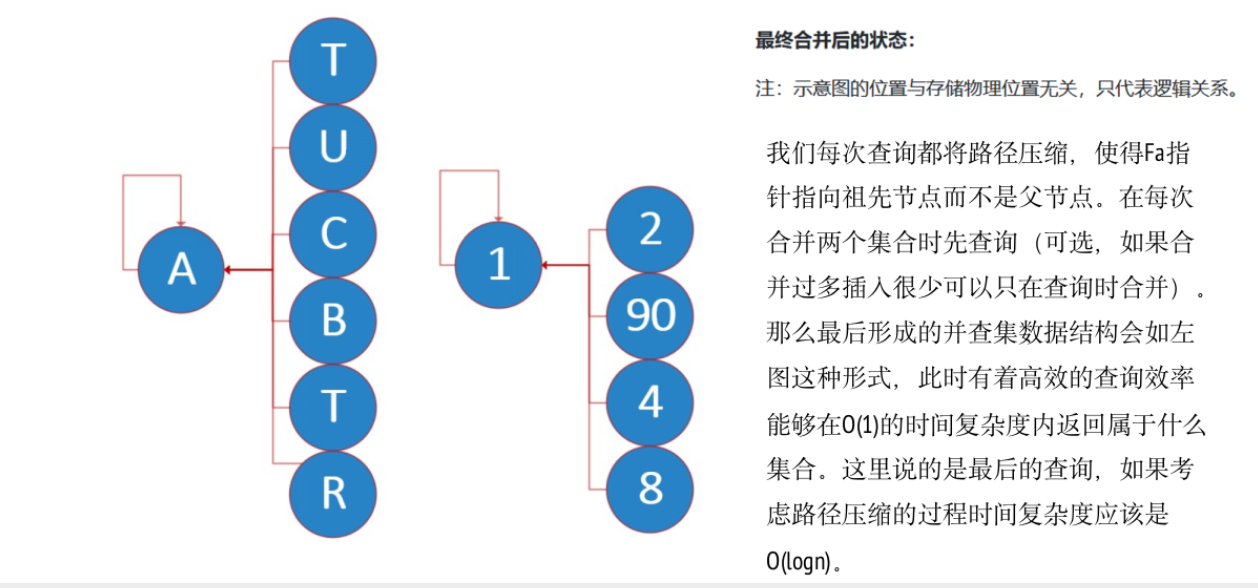
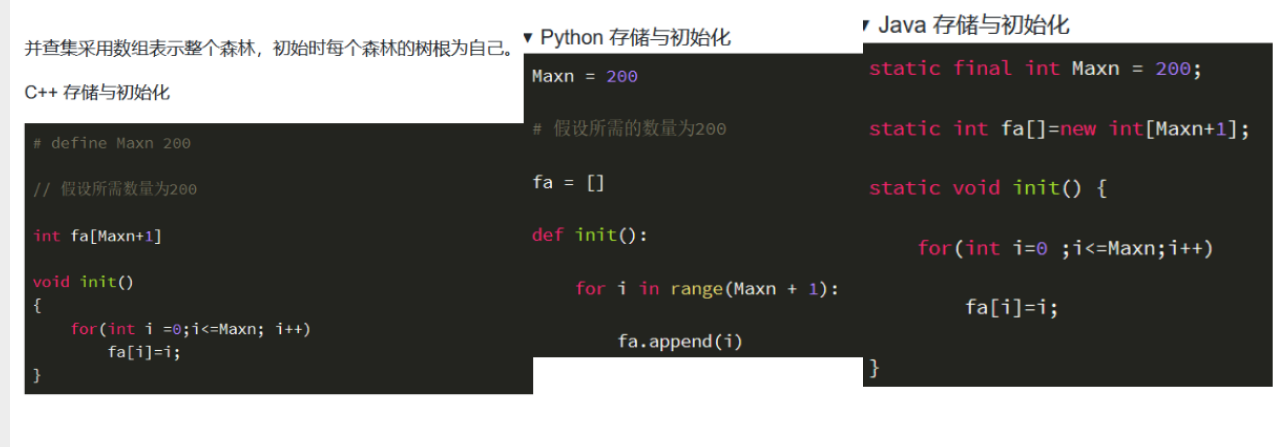

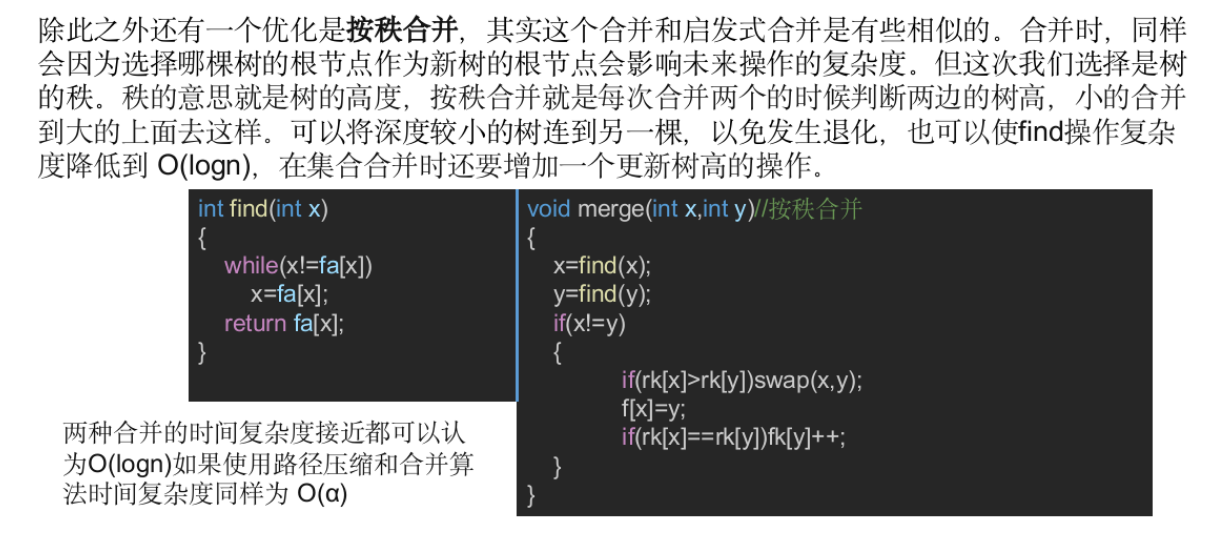

可撤销并查集定义




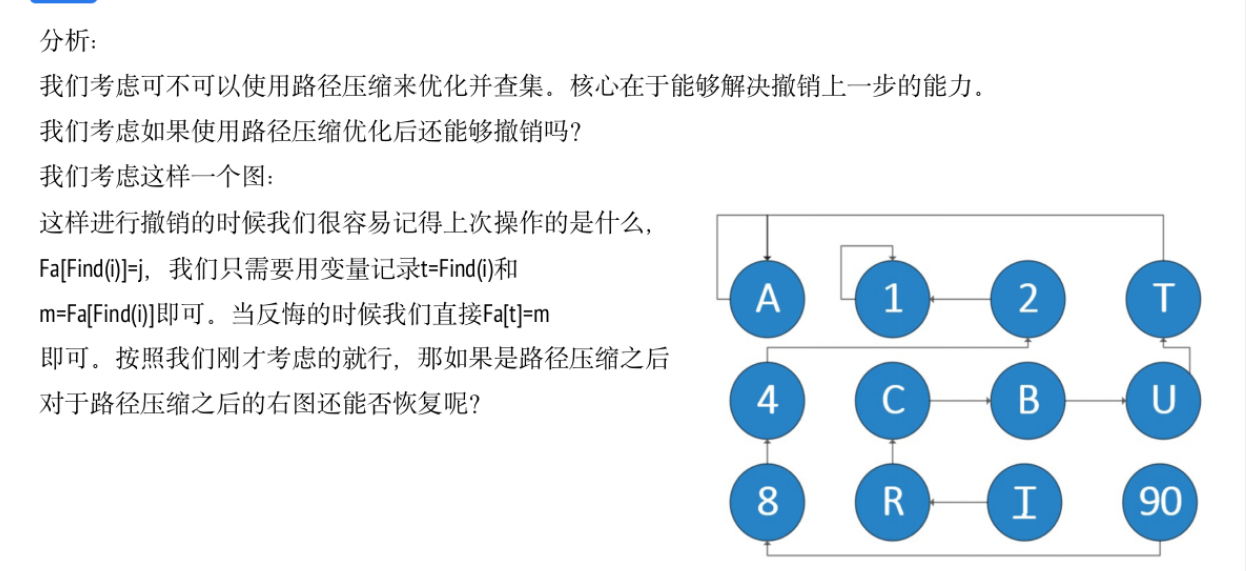
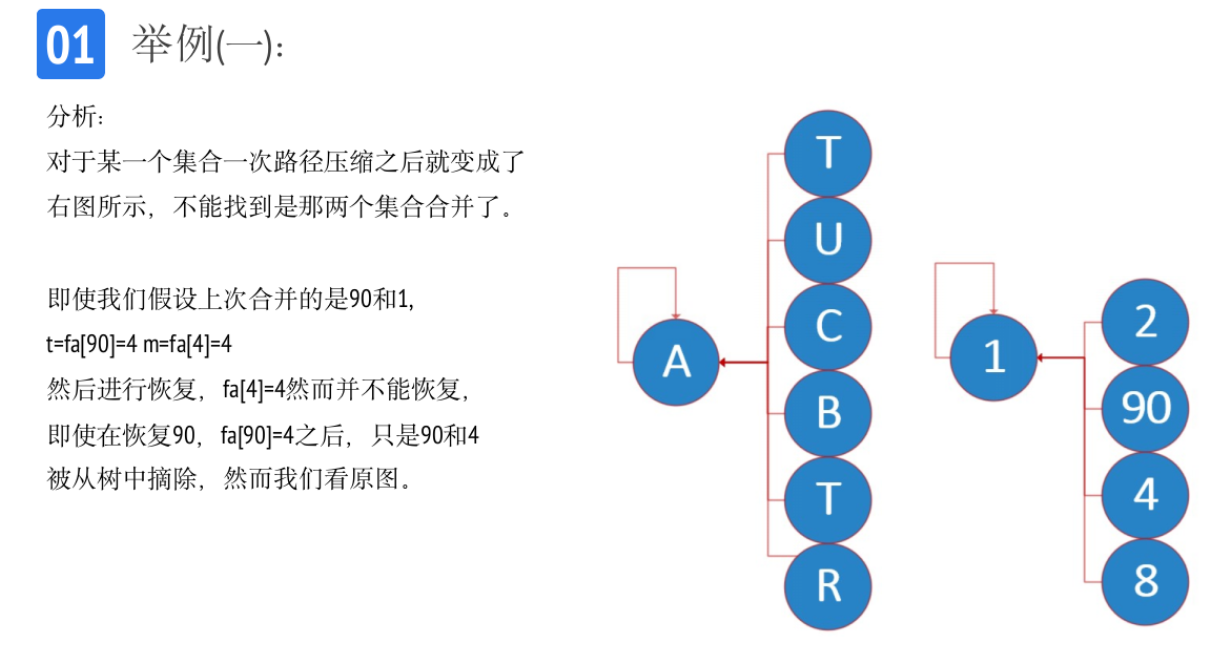
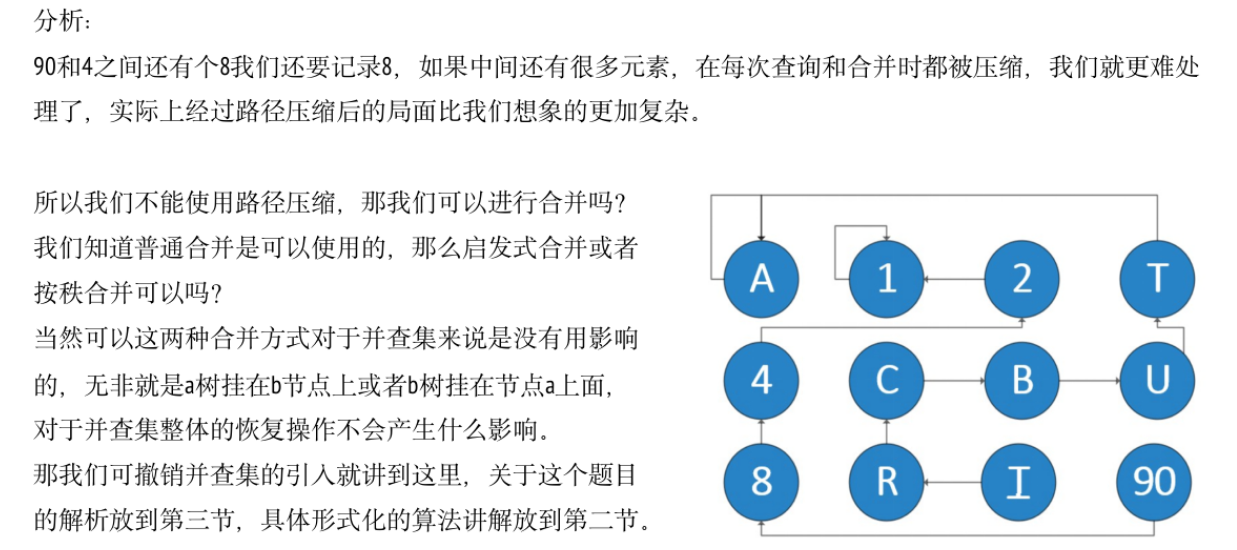


算法原理


带权并查集





树上问题
树的基本概念
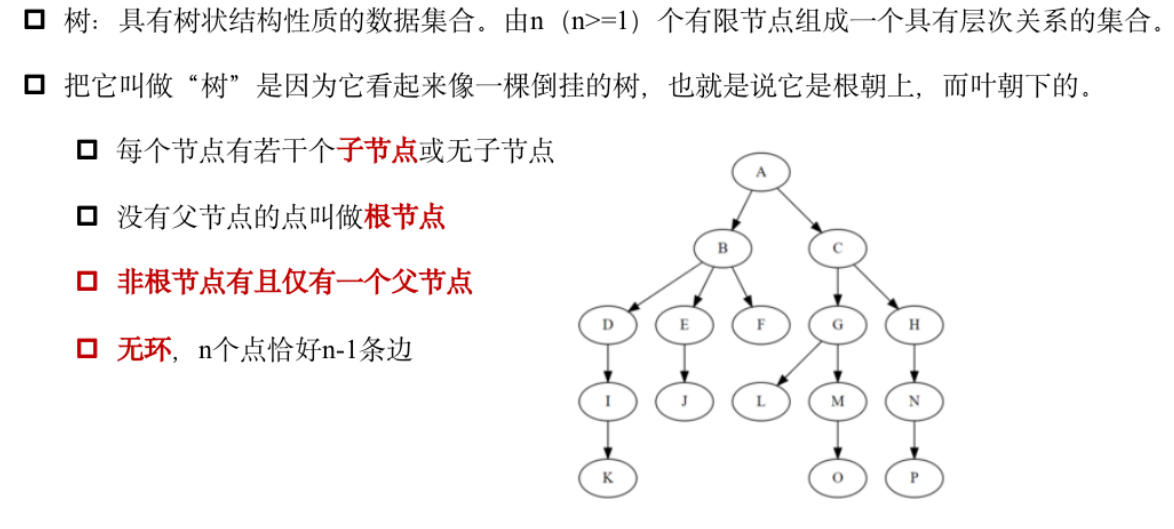
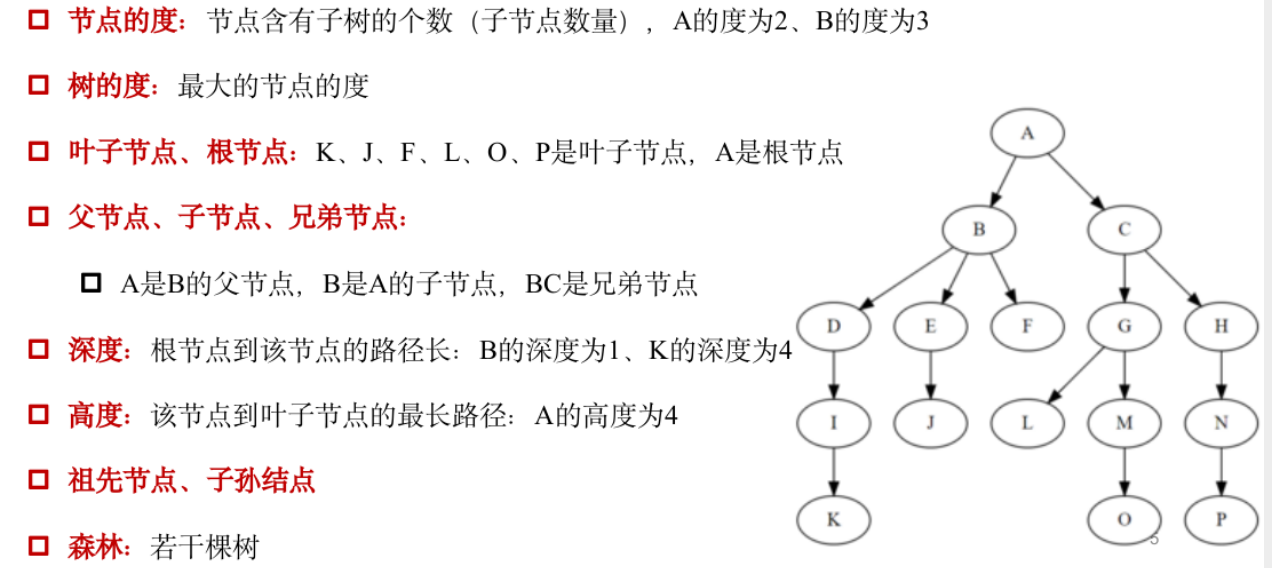
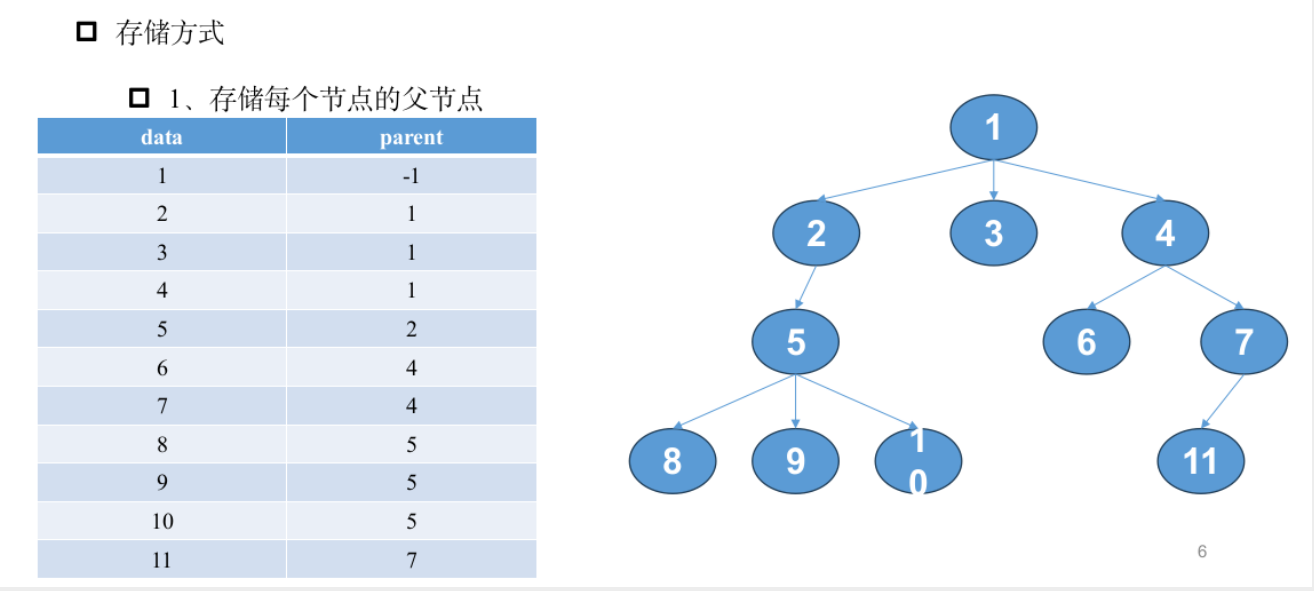
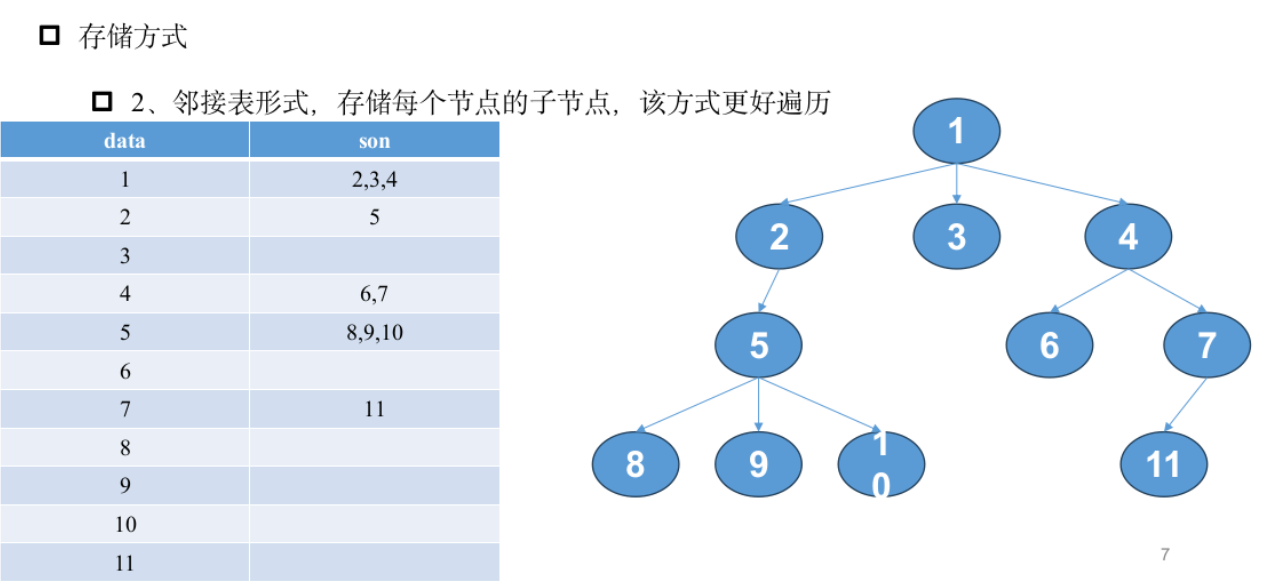
二叉树
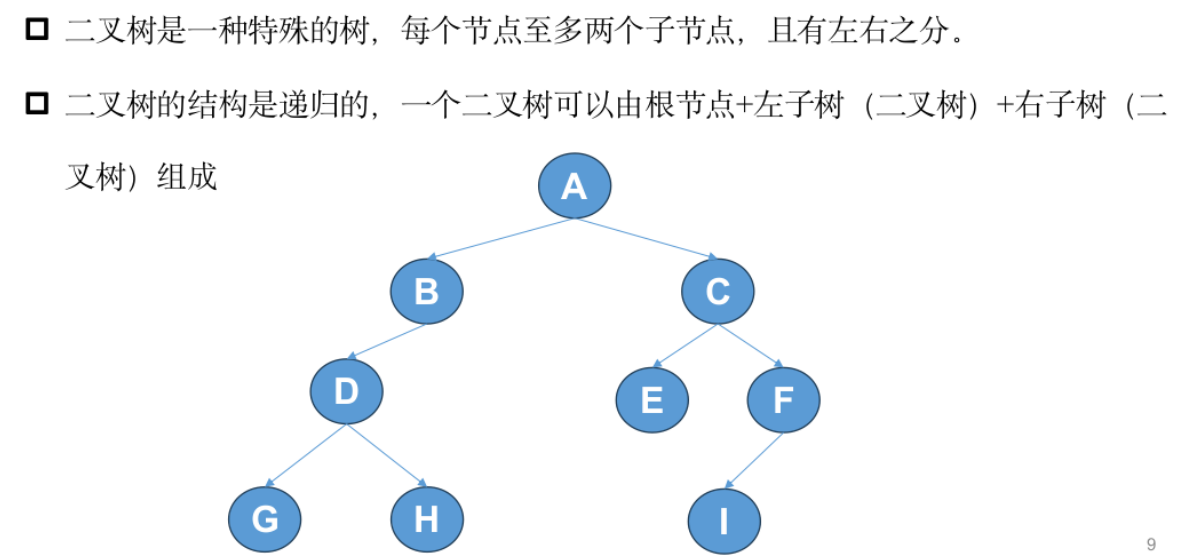
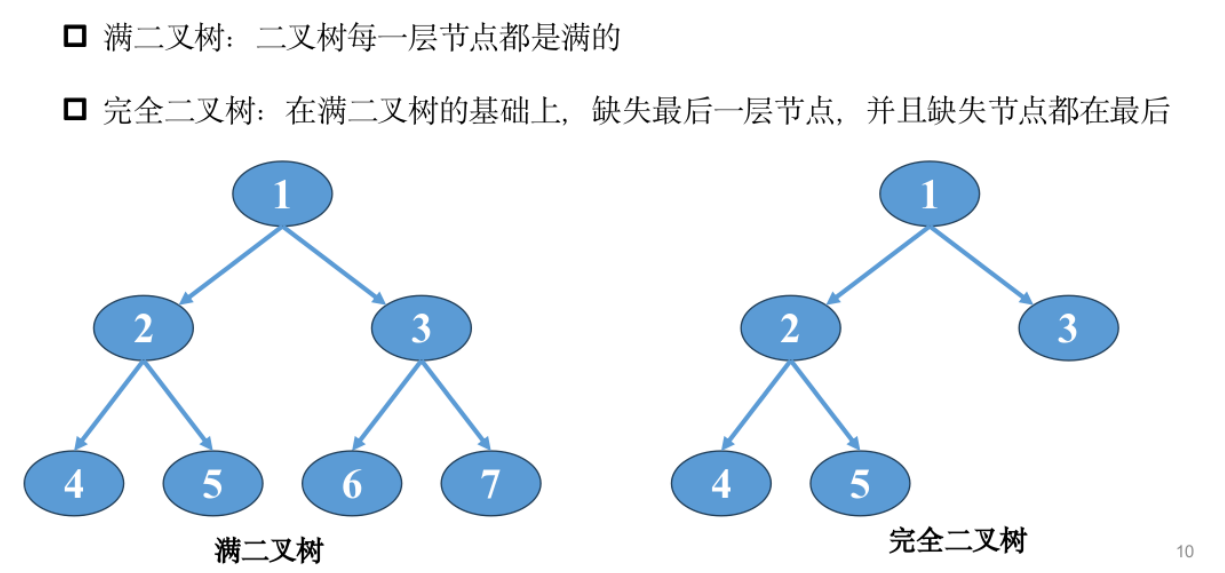
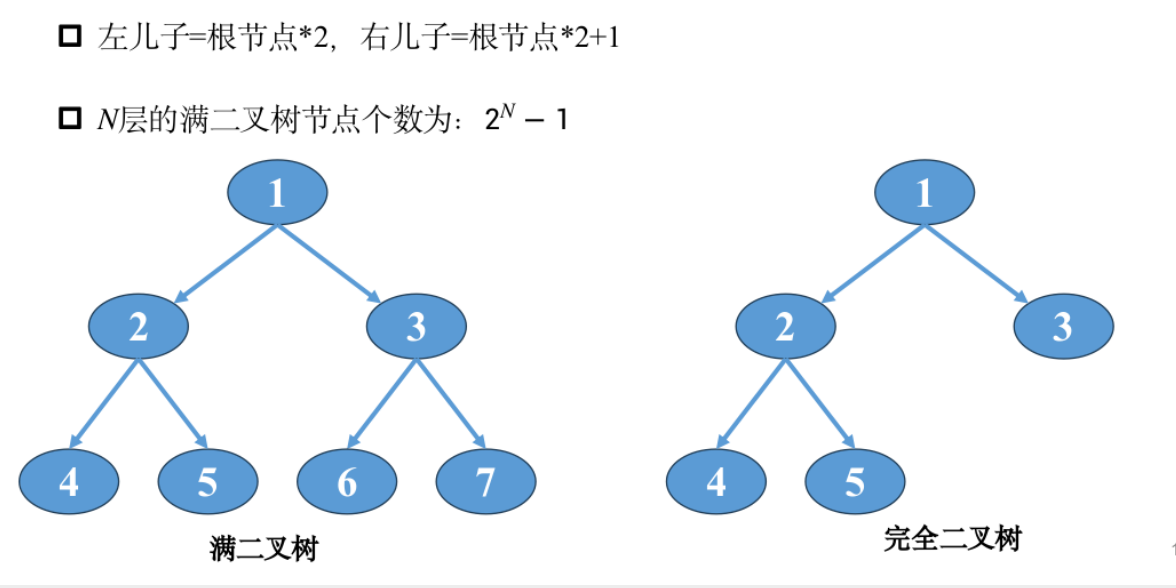
模板题——完全二叉树的权值
1 | |

树的遍历

先序遍历
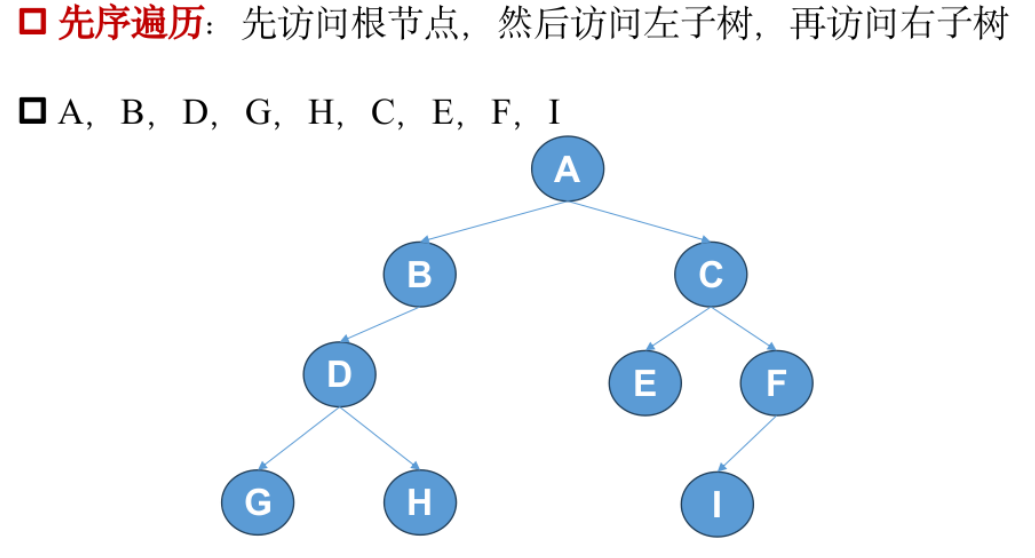
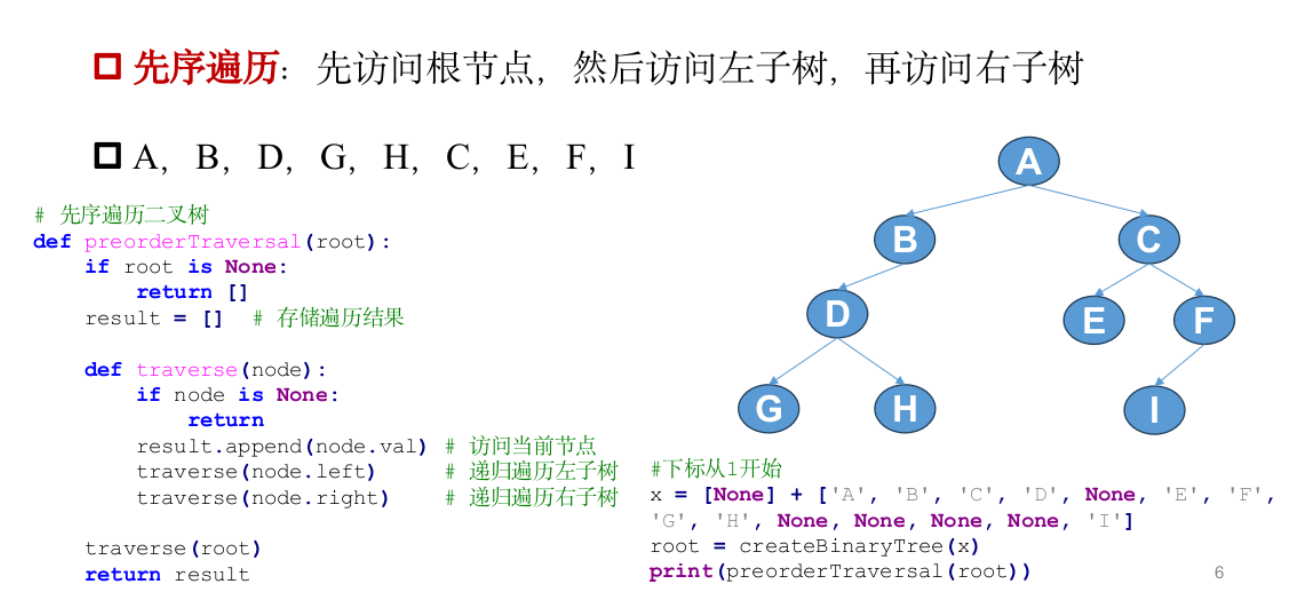
中序遍历
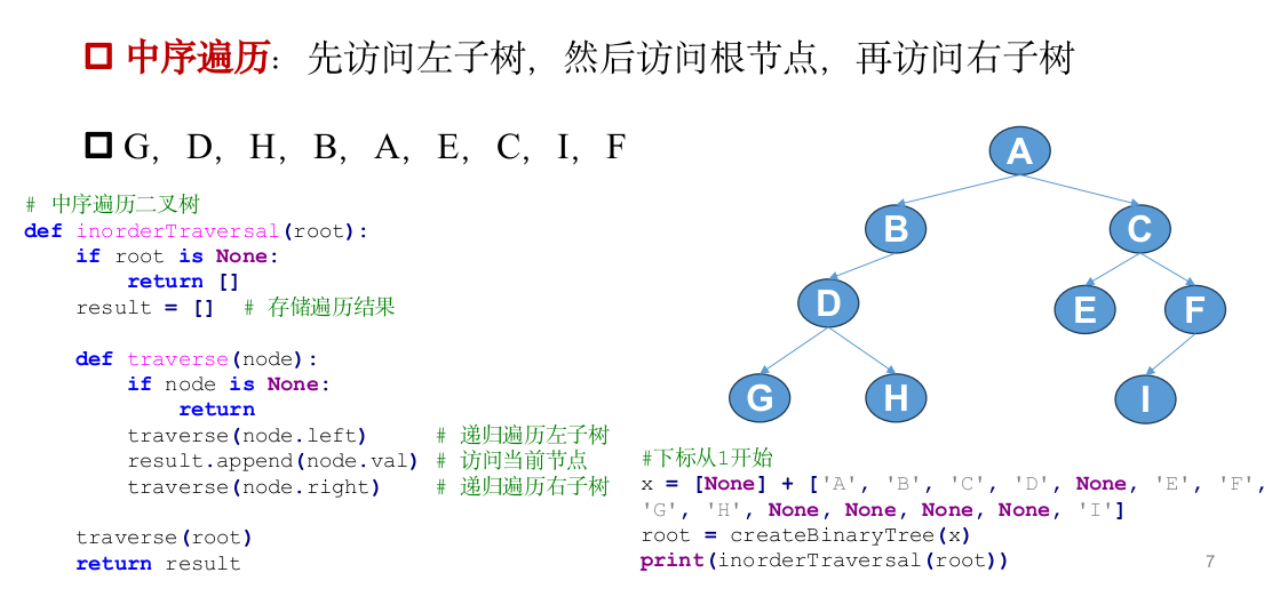
后序遍历
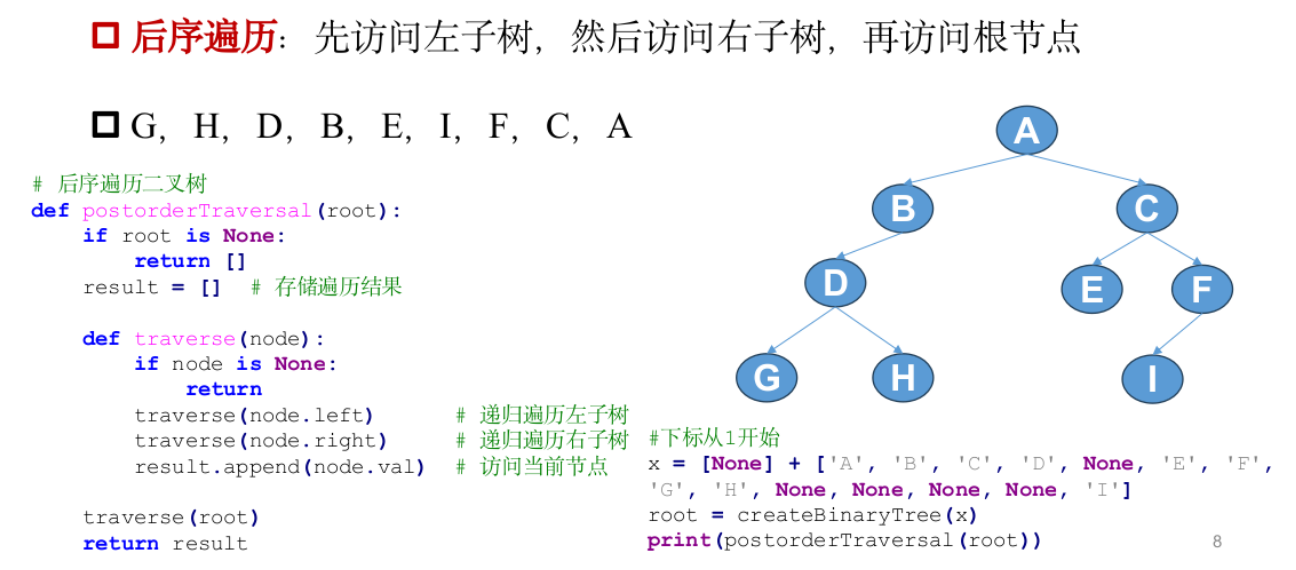
层序遍历
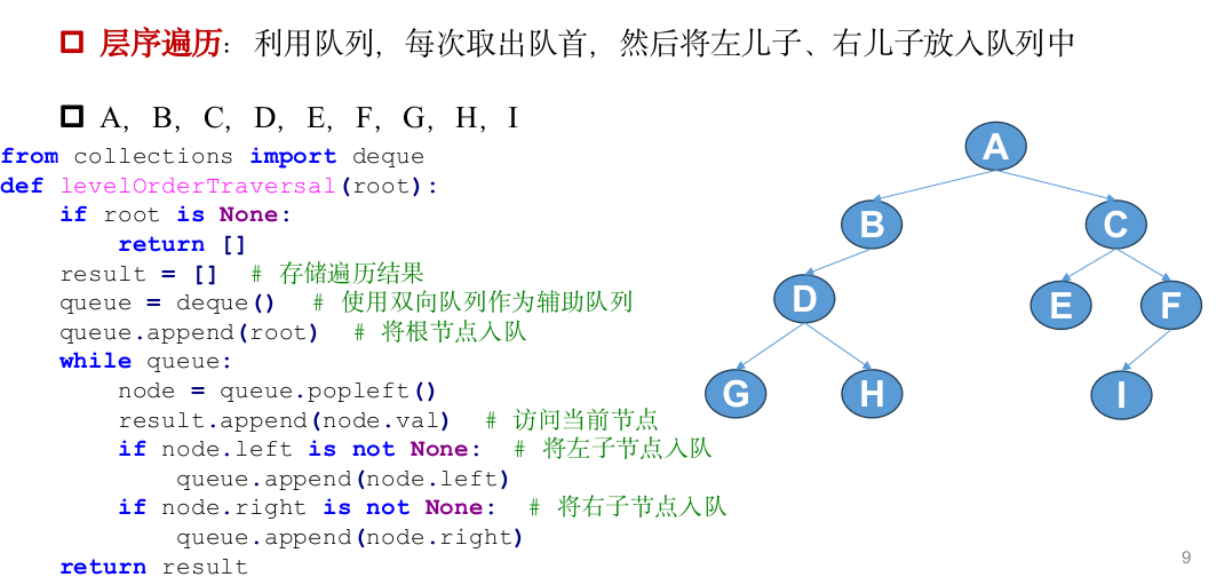
树的遍历
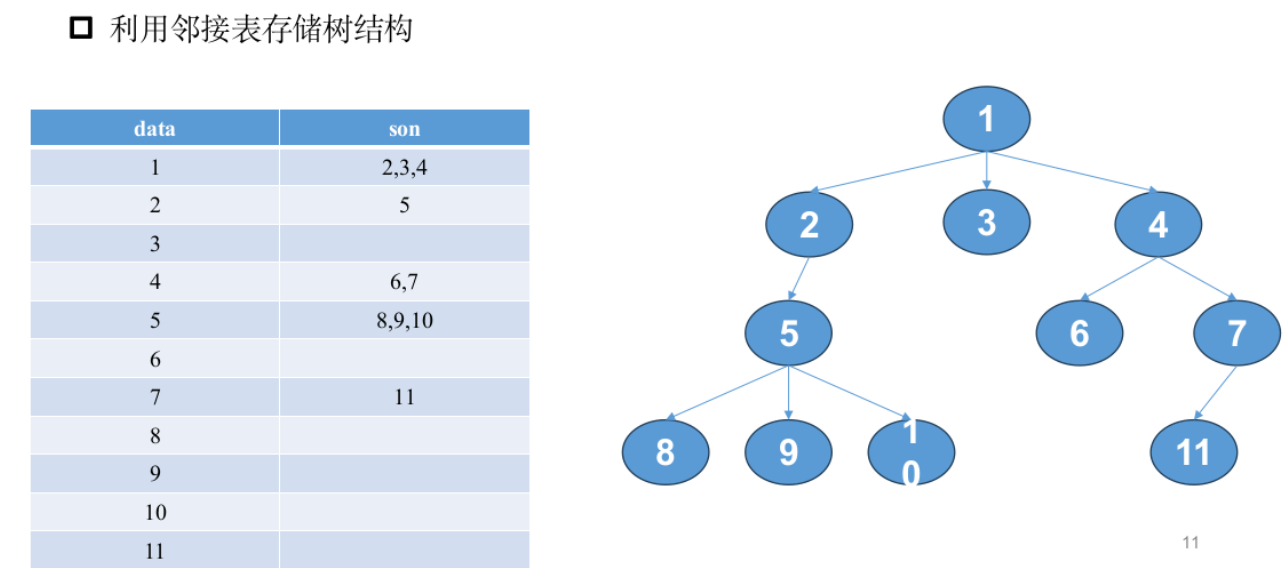
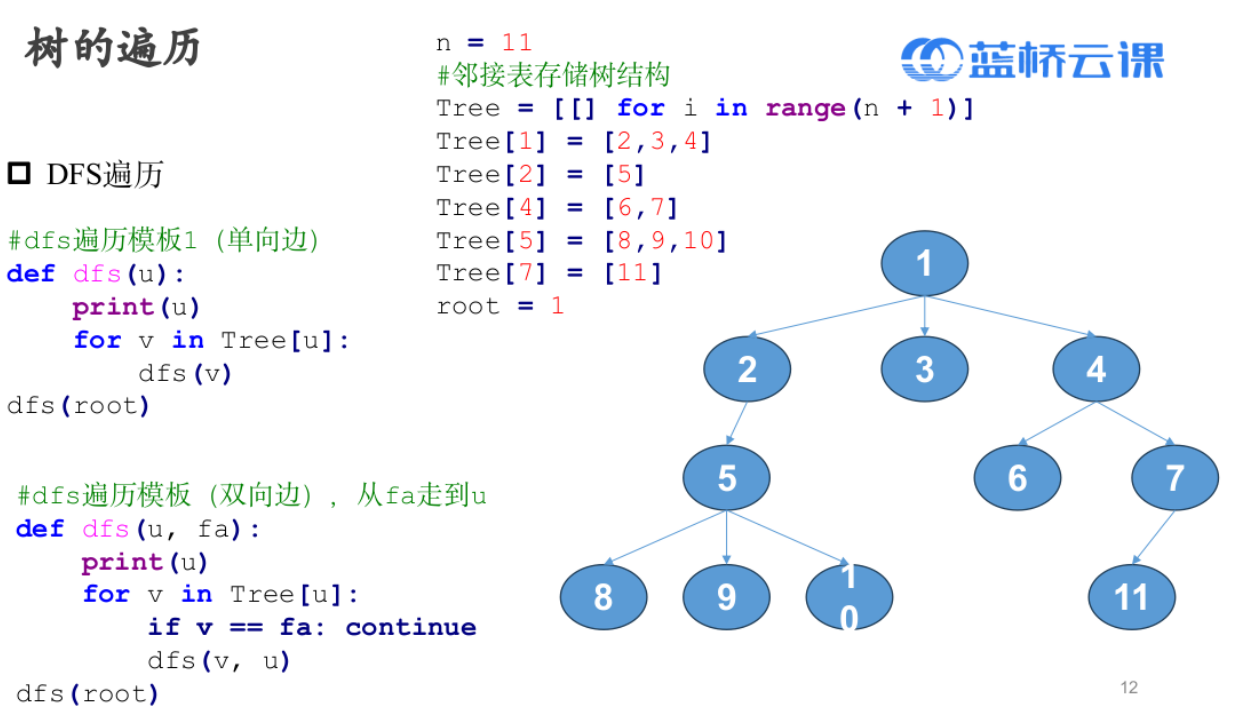
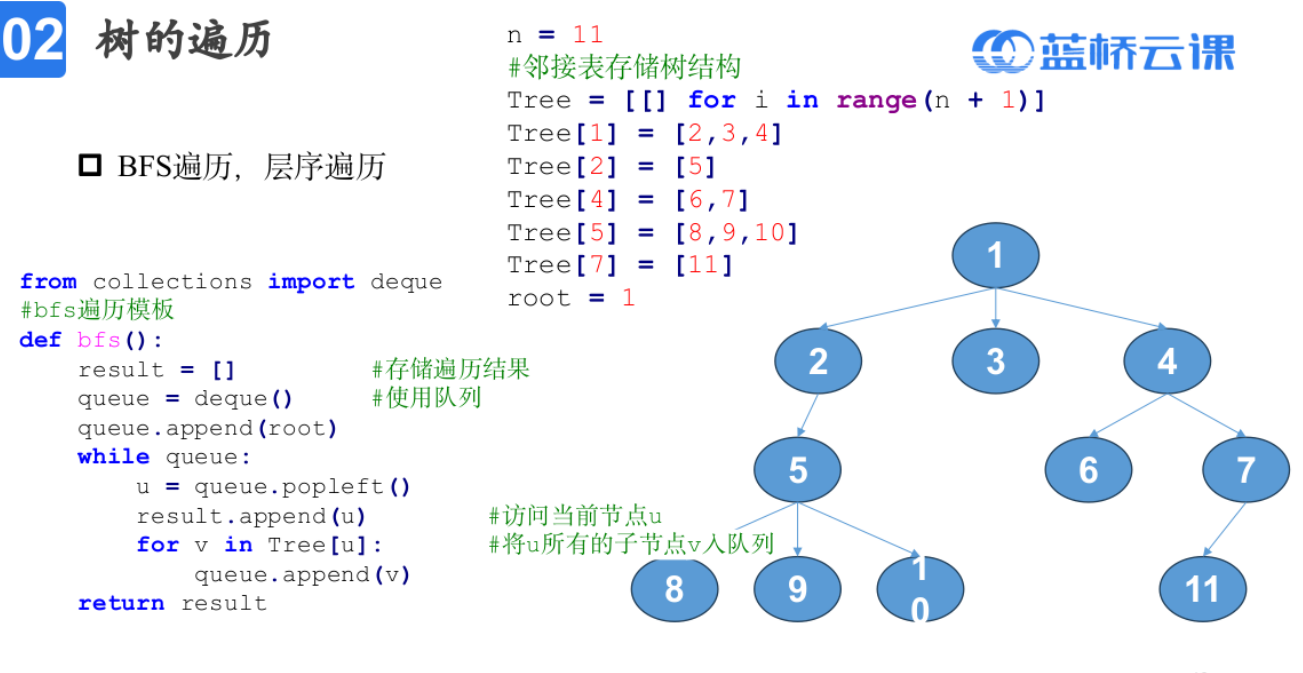
模板题——欧涛爬树
1 | |
1 | |
树的直径与重心
树的直径

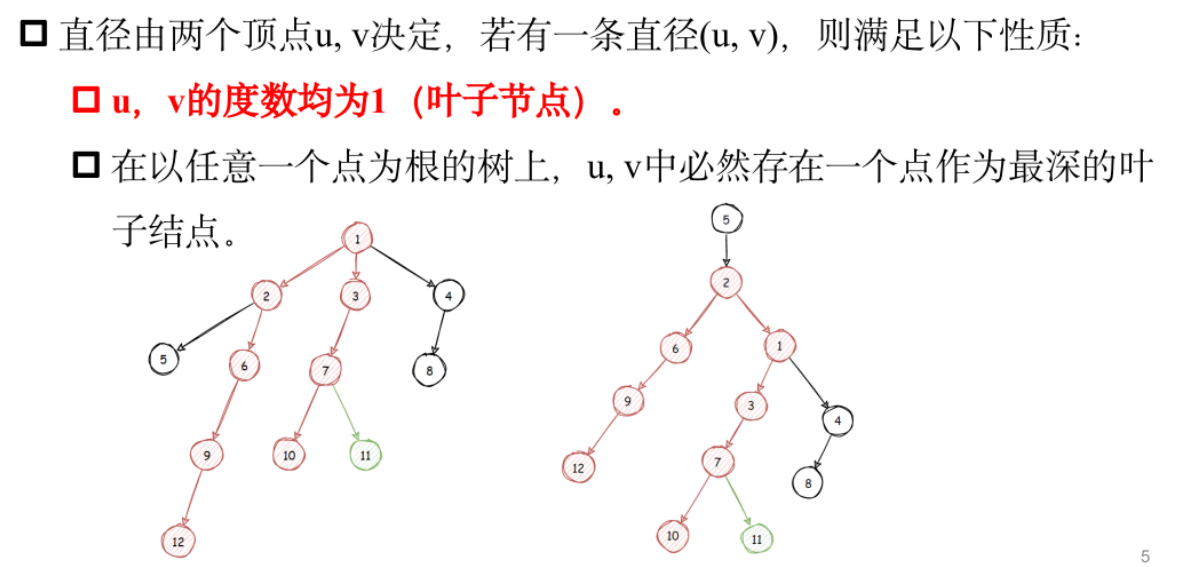
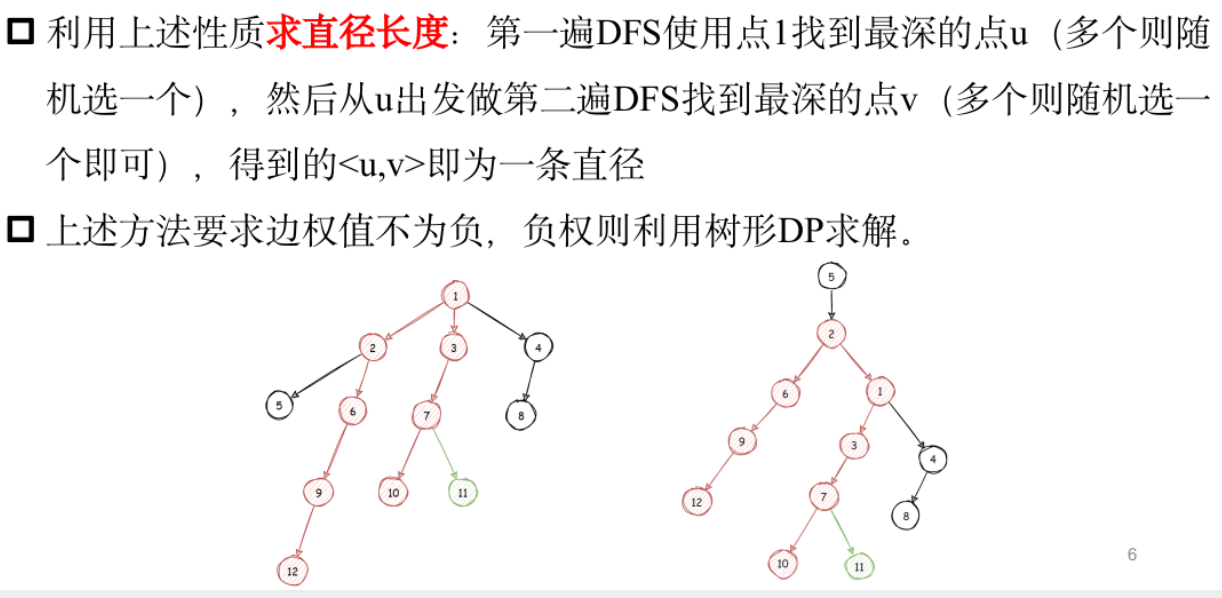
模板题——直径
1 | |

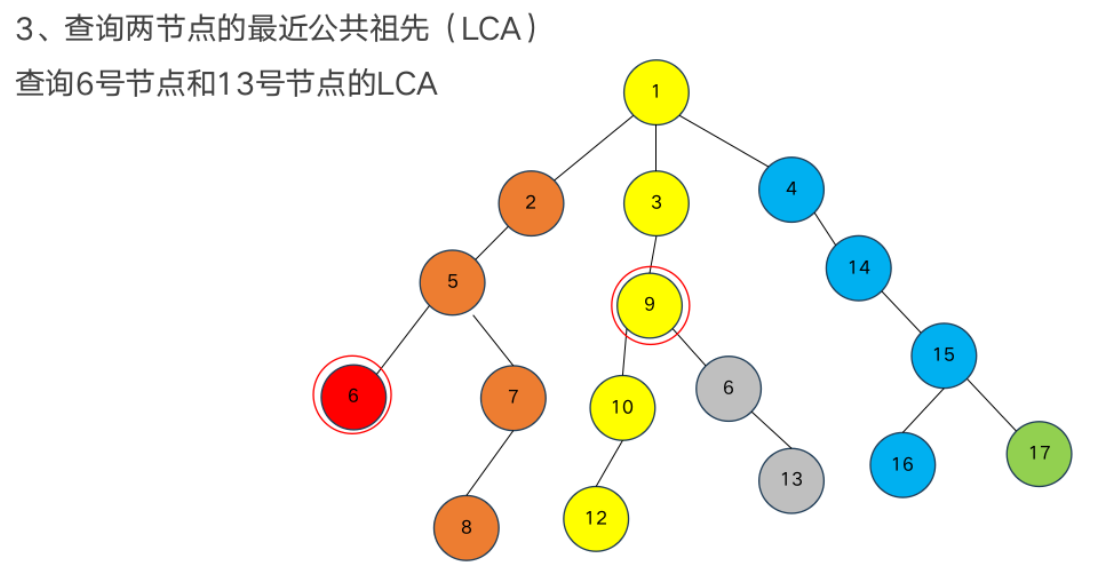
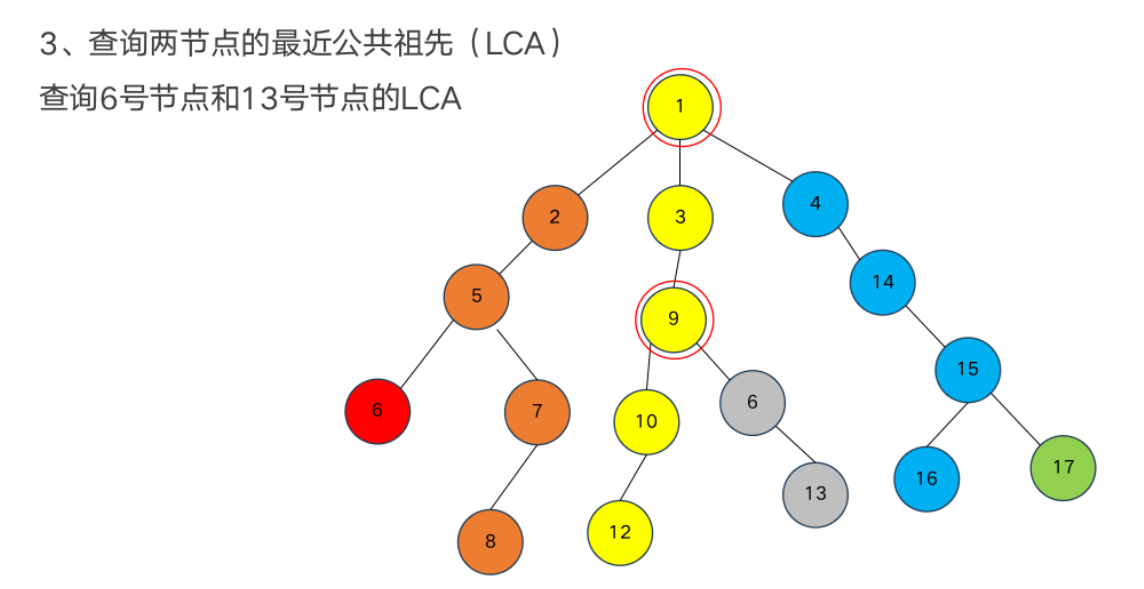
LCA
最近公共祖先






模板题——最近公共祖先LCA查询
1 | |
树上差分




问题引入

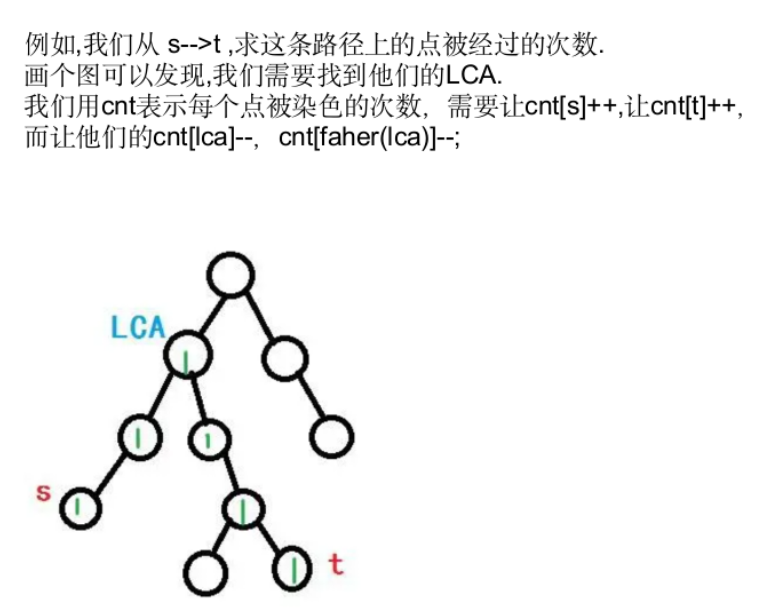

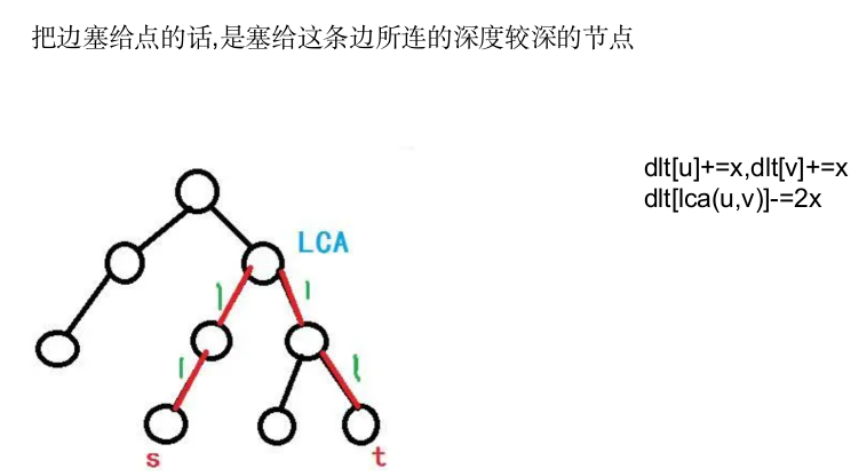


模板题——
1 | |
DFS序
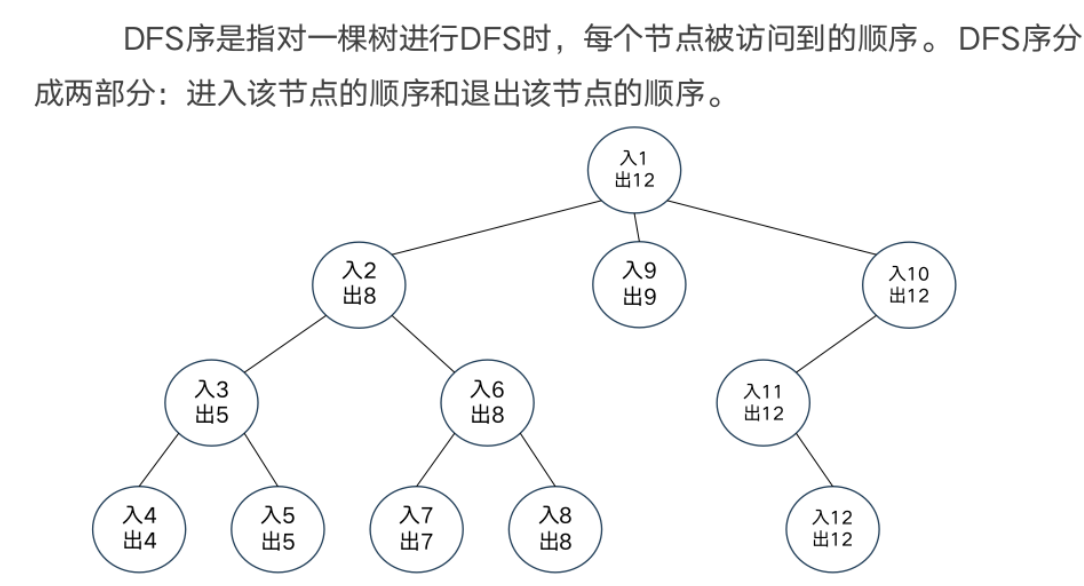

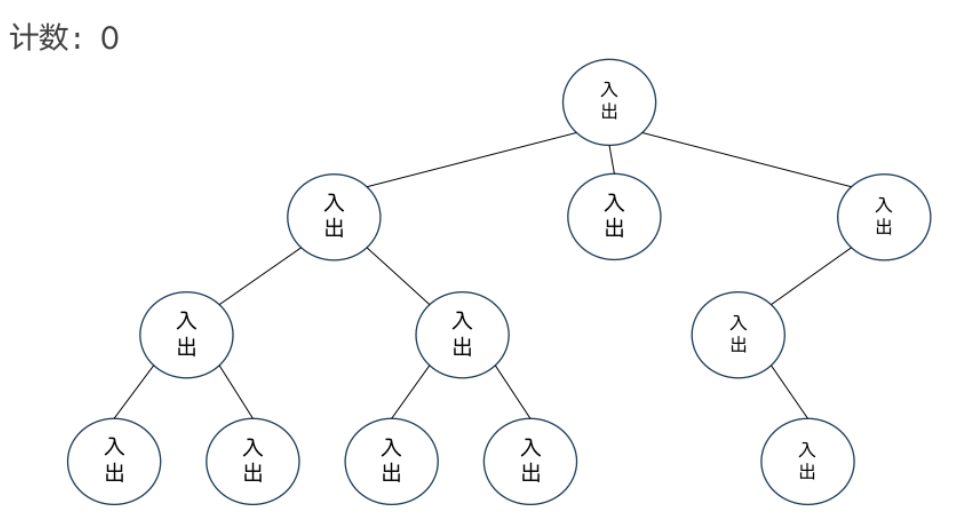
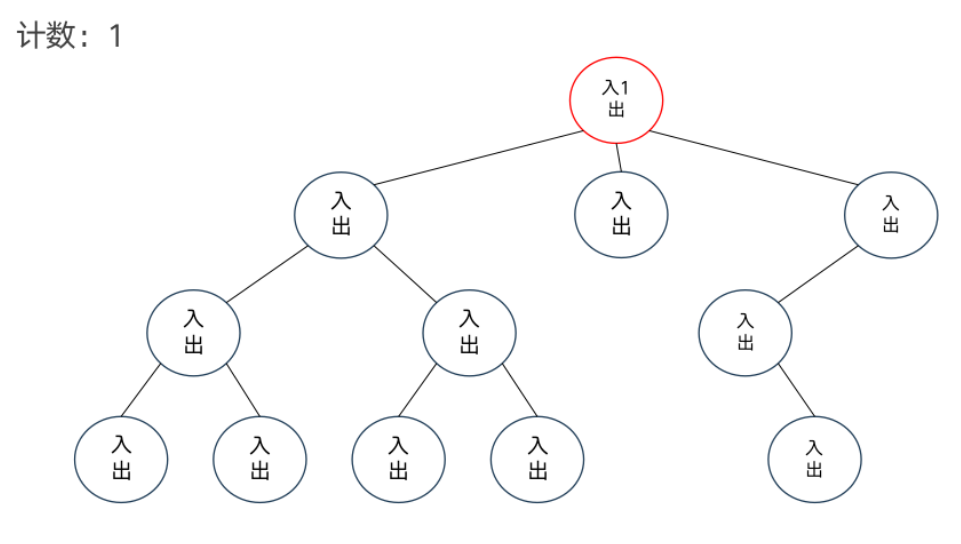
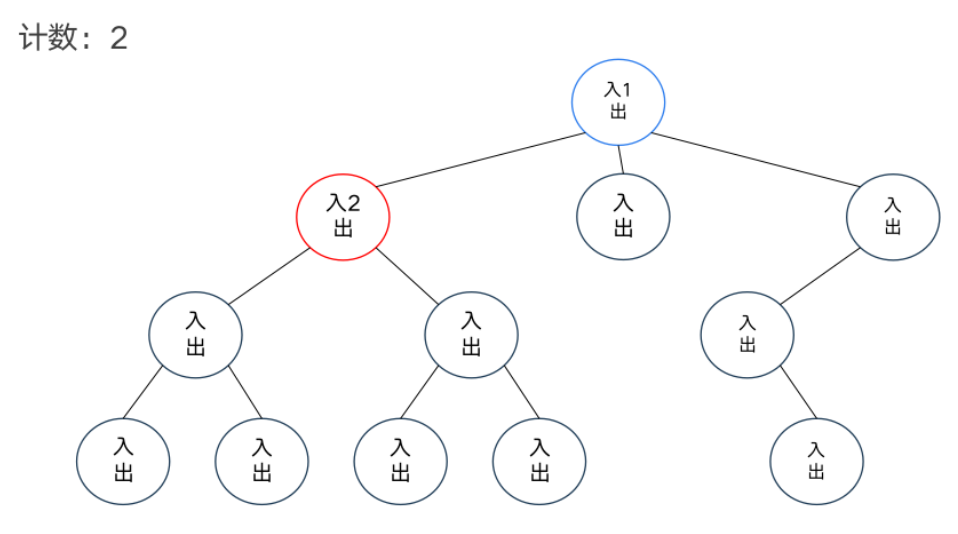
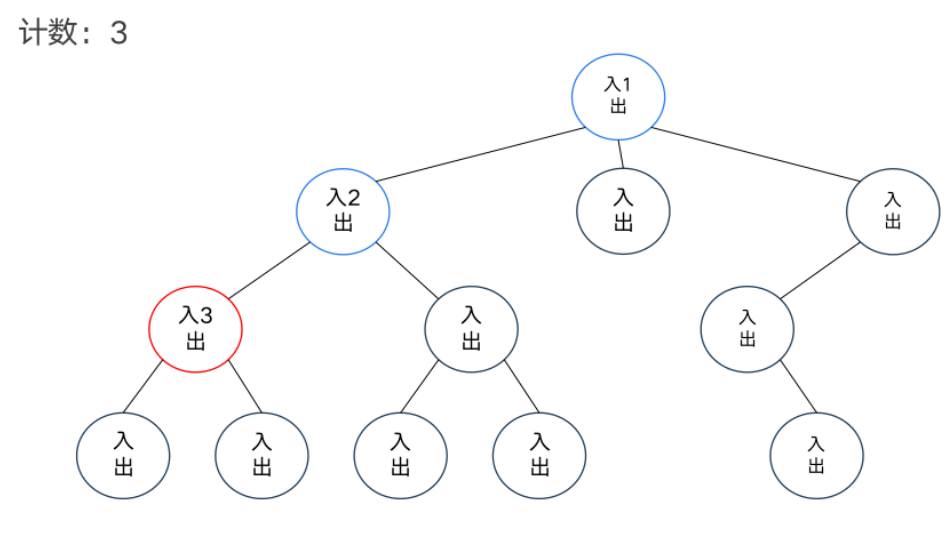
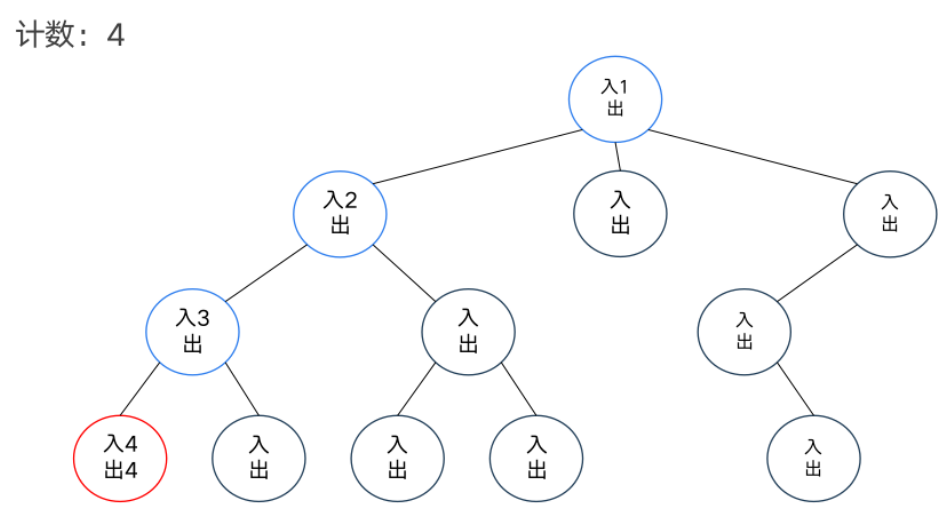
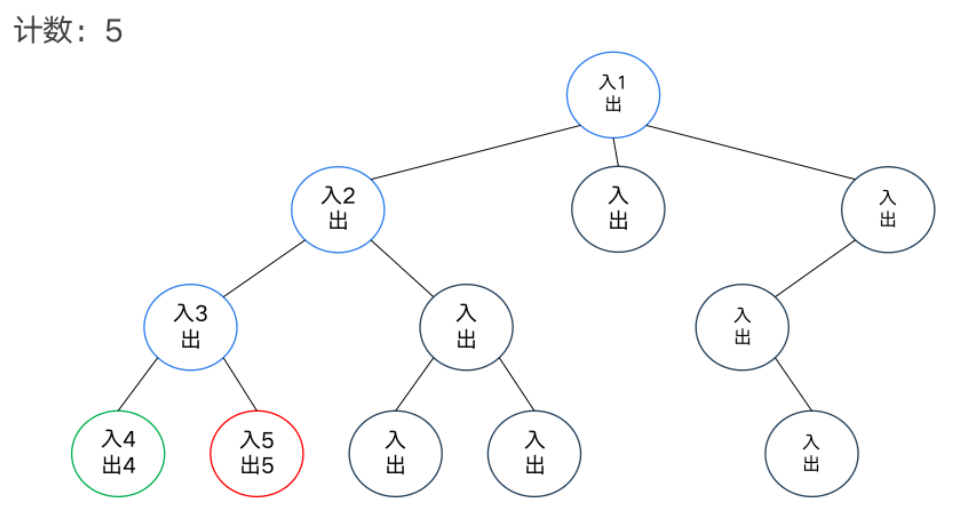
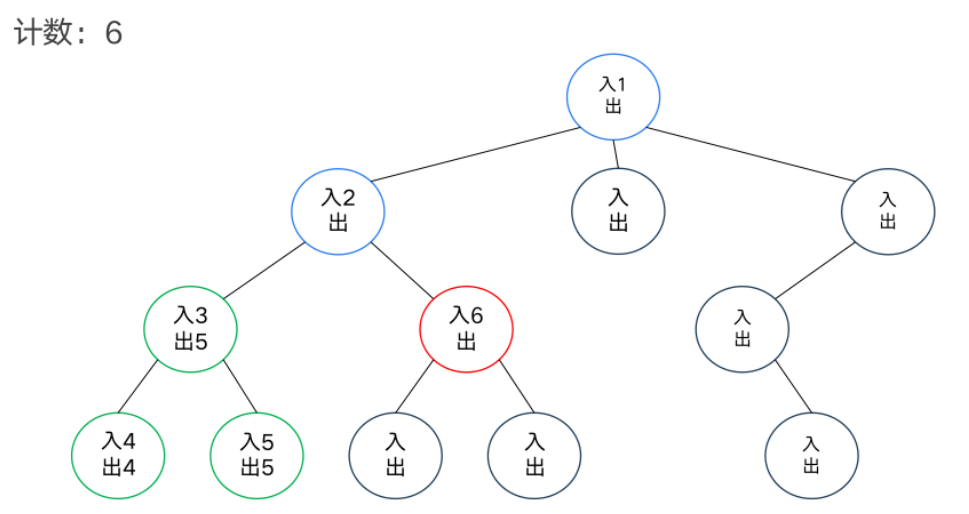
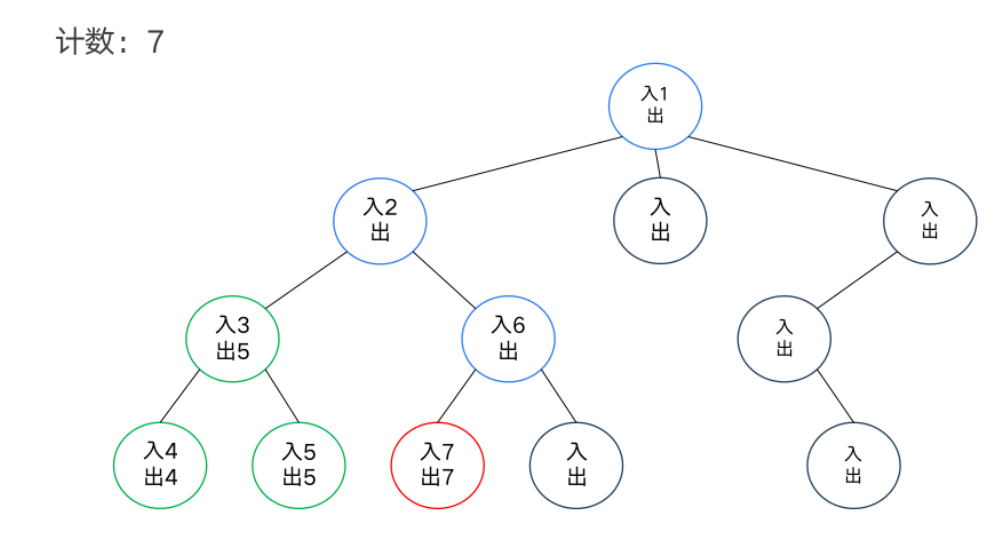
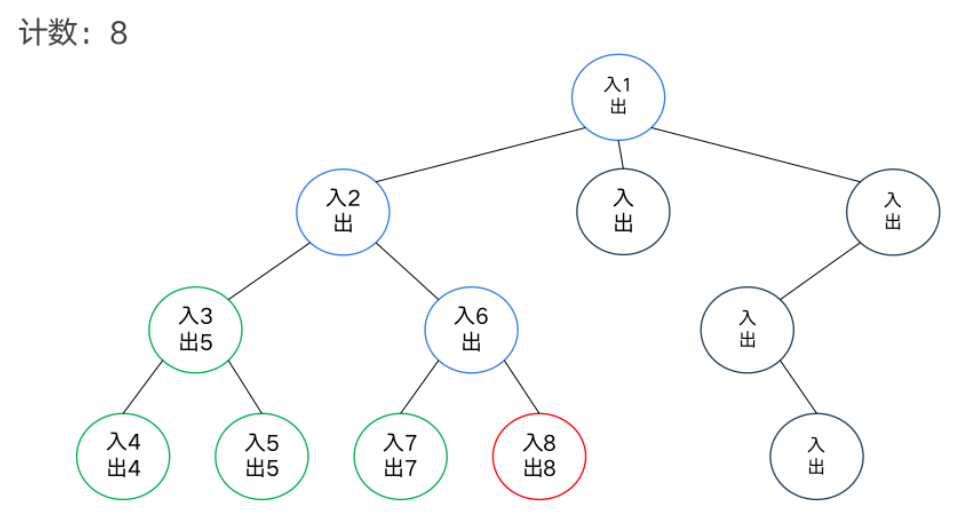
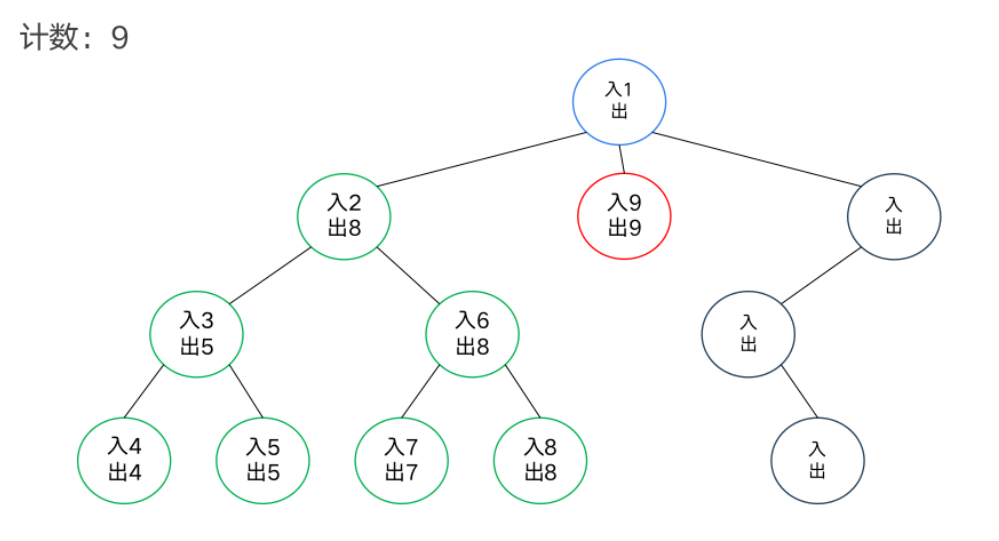
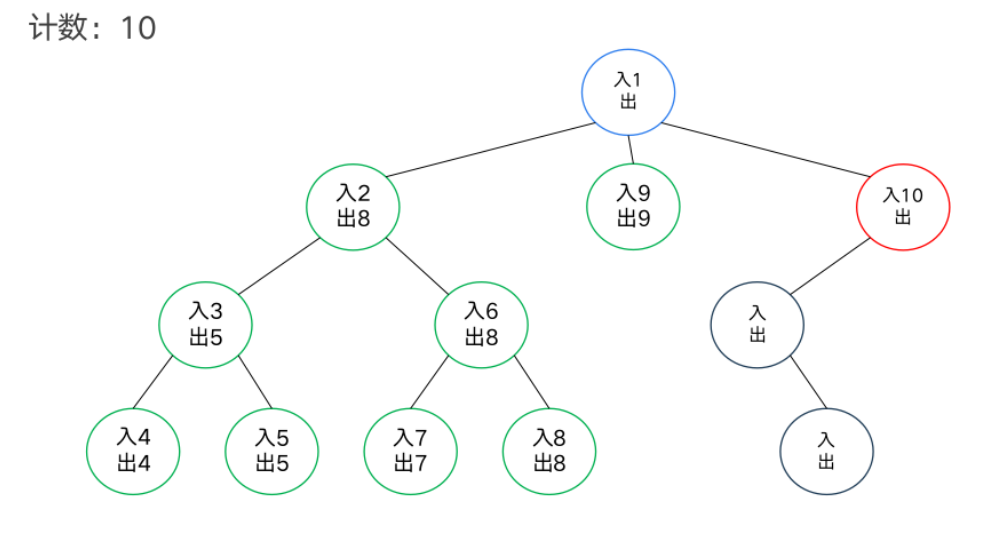
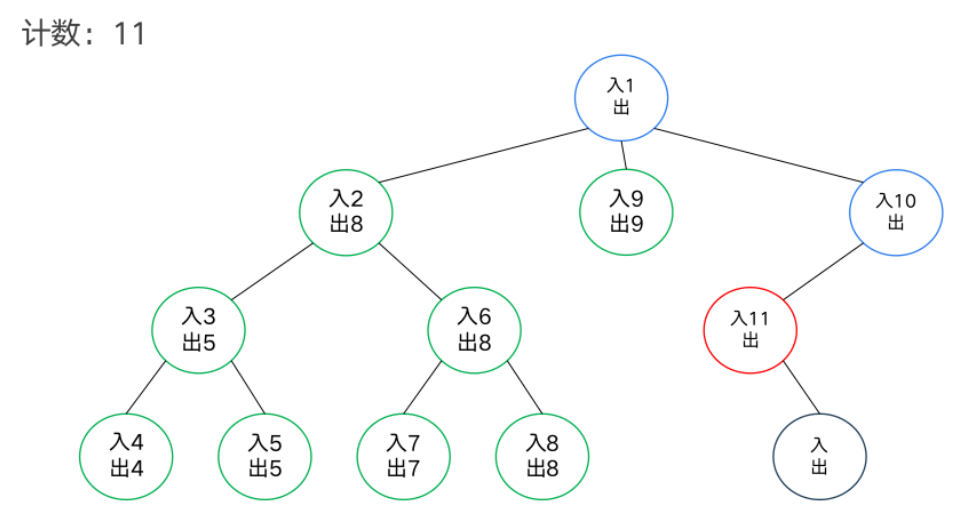
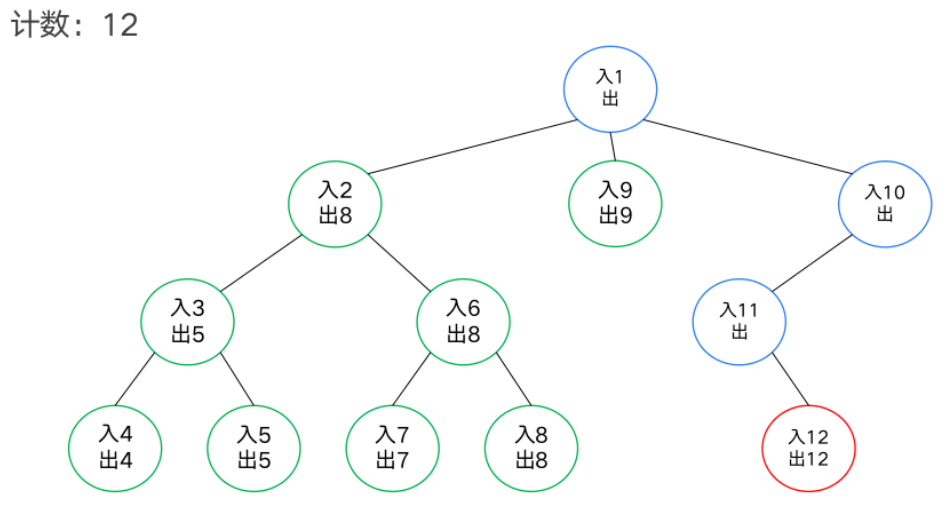
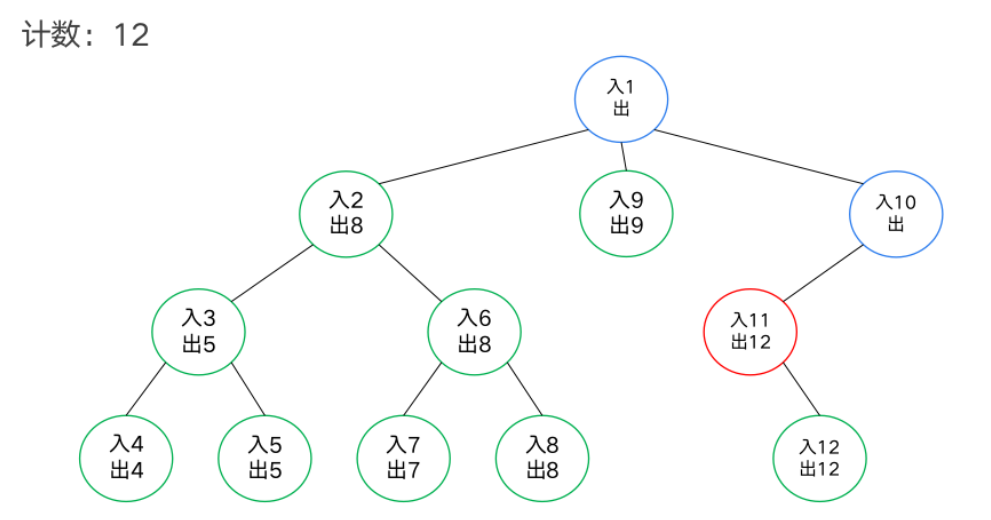
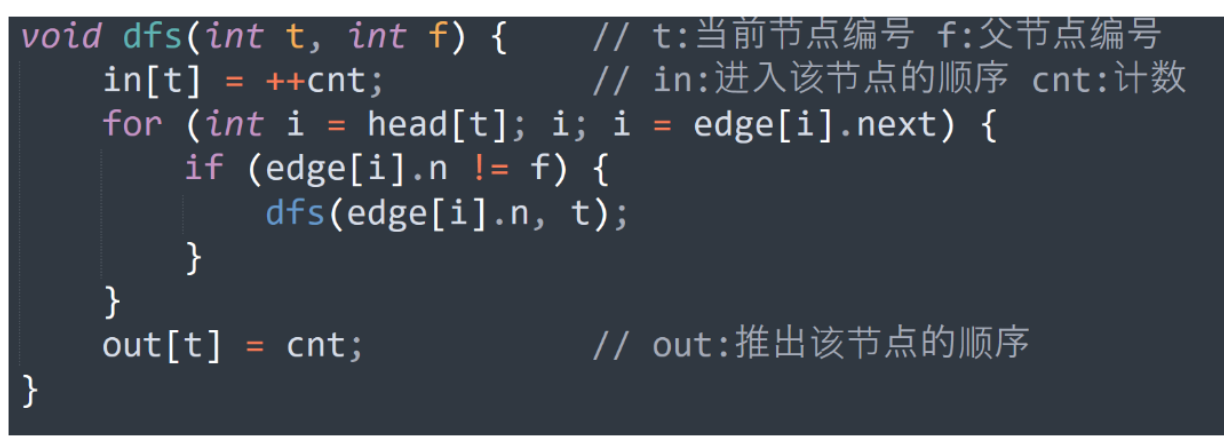
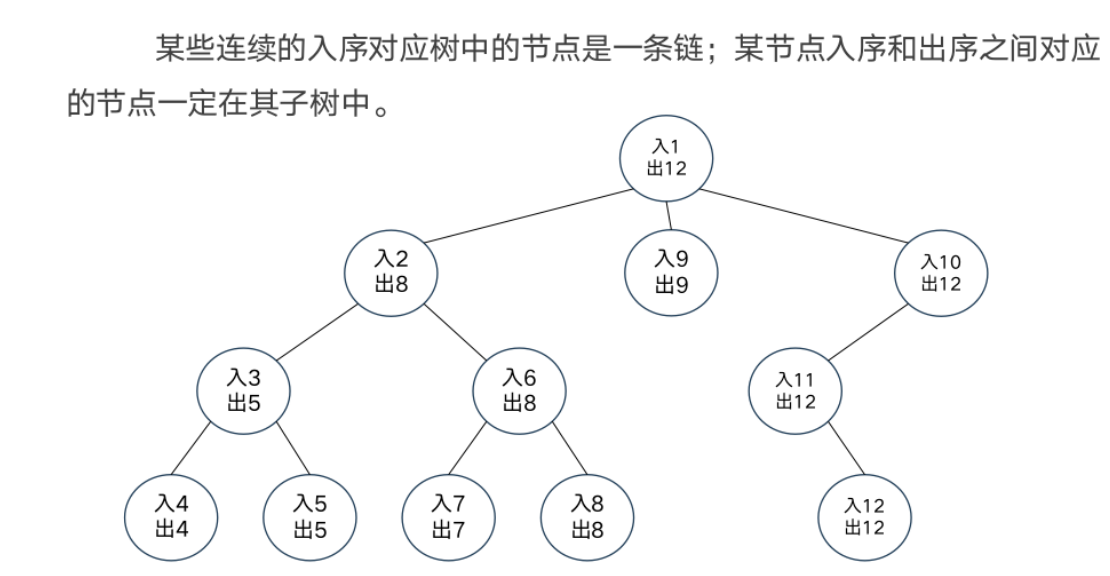
模板题——异或和
dfs序和树状数组
1 | |
模拟暴力代码
1 | |
利用邻接表打印树结构,然后根据子树根节点寻找打印子树的元素,存到列表中,最后对列表的所有元素(即子树的所有点)进行异或和运算
1 | |
树链剖分

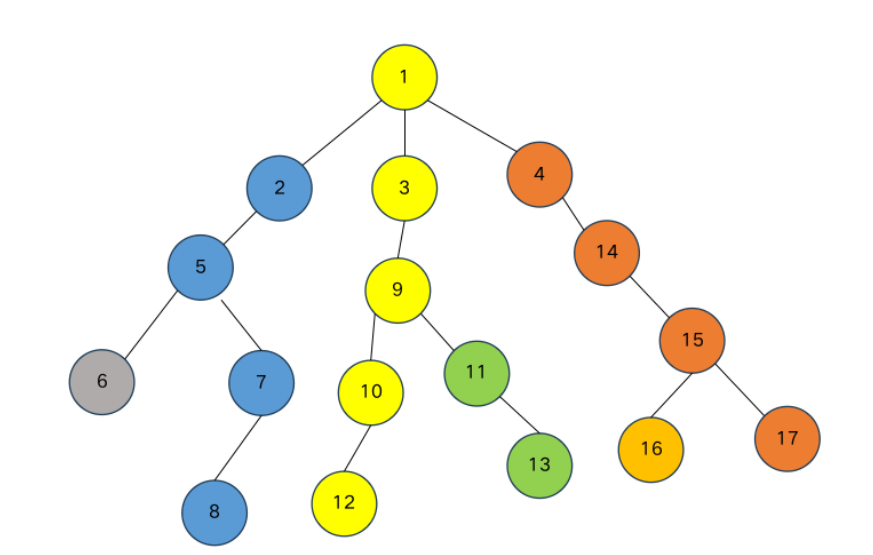
重链部分




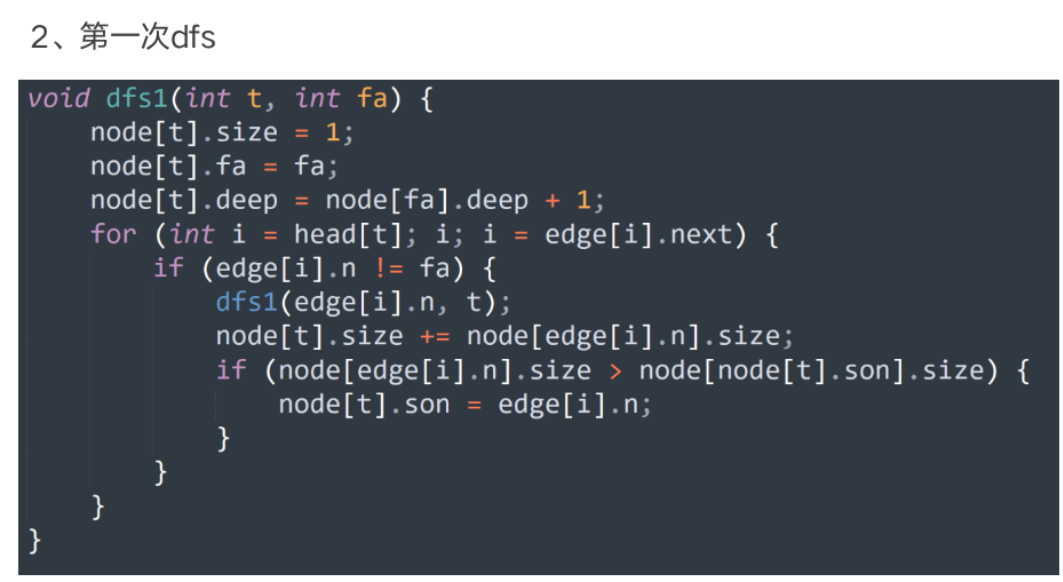

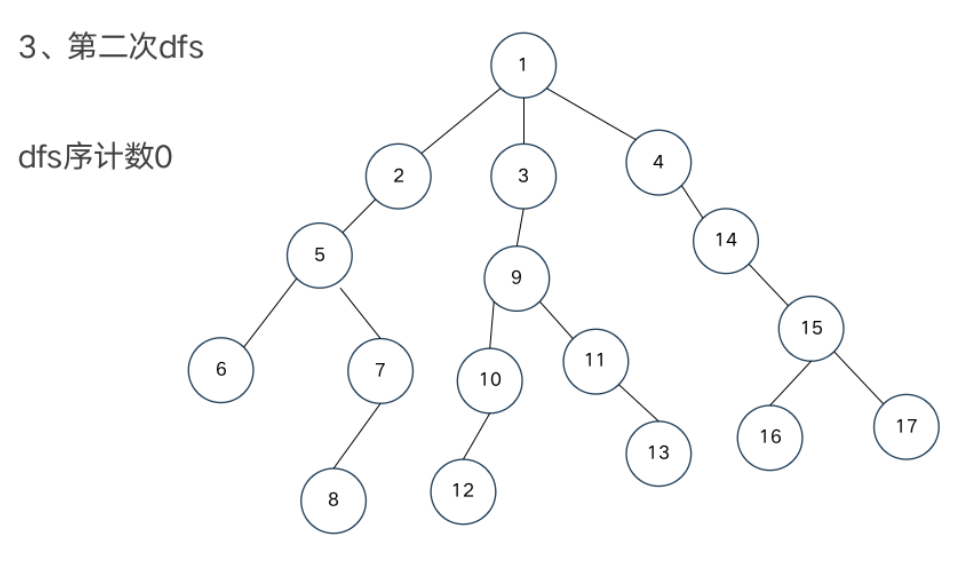
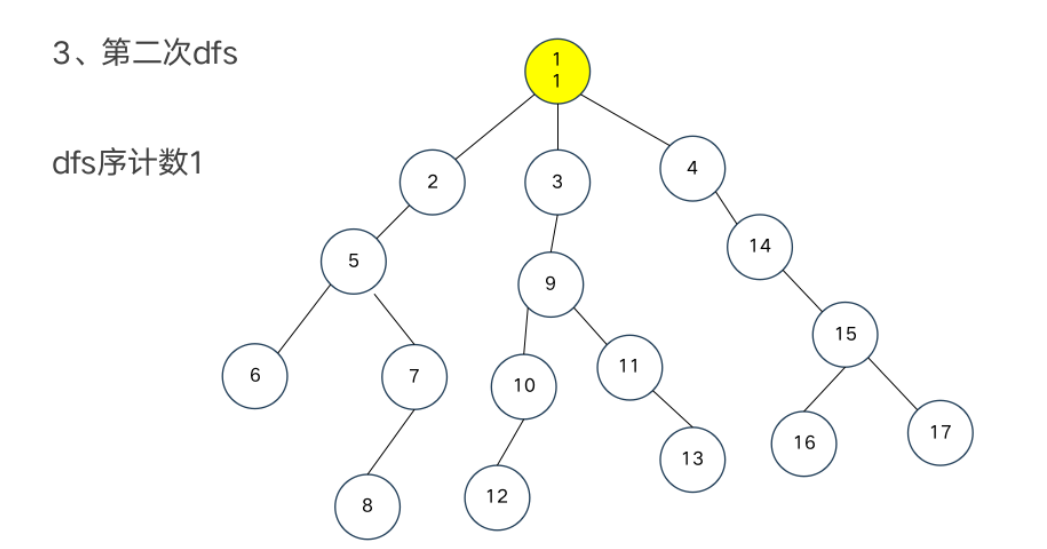
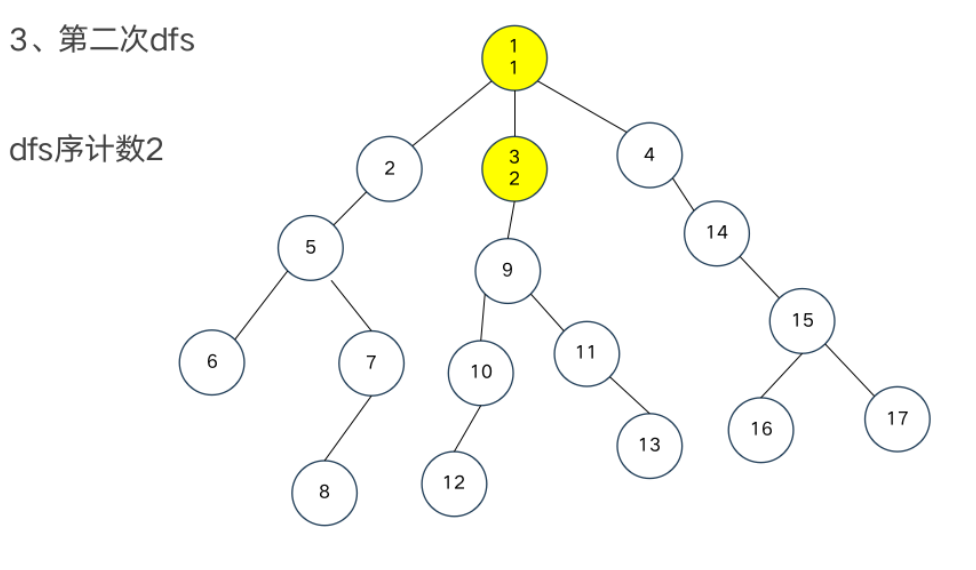
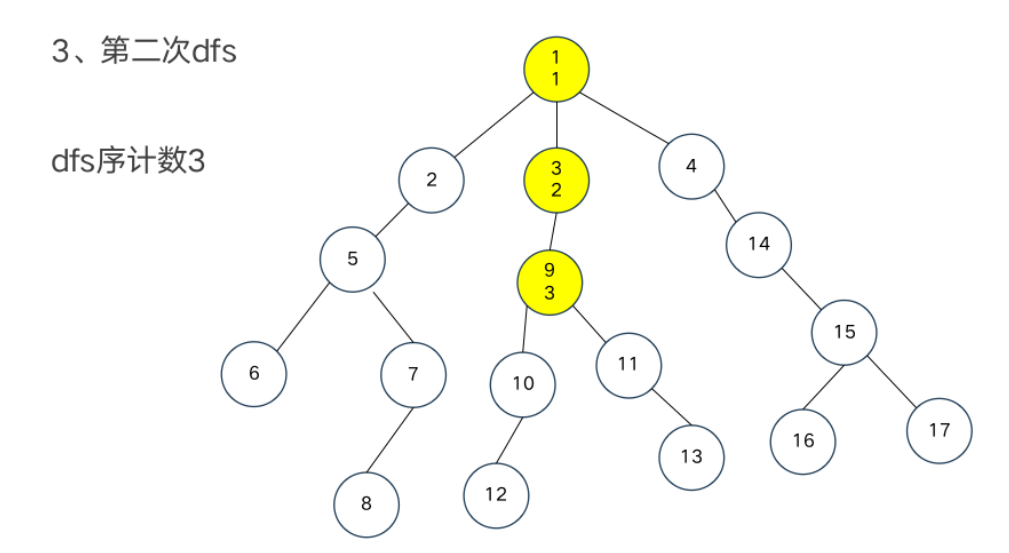
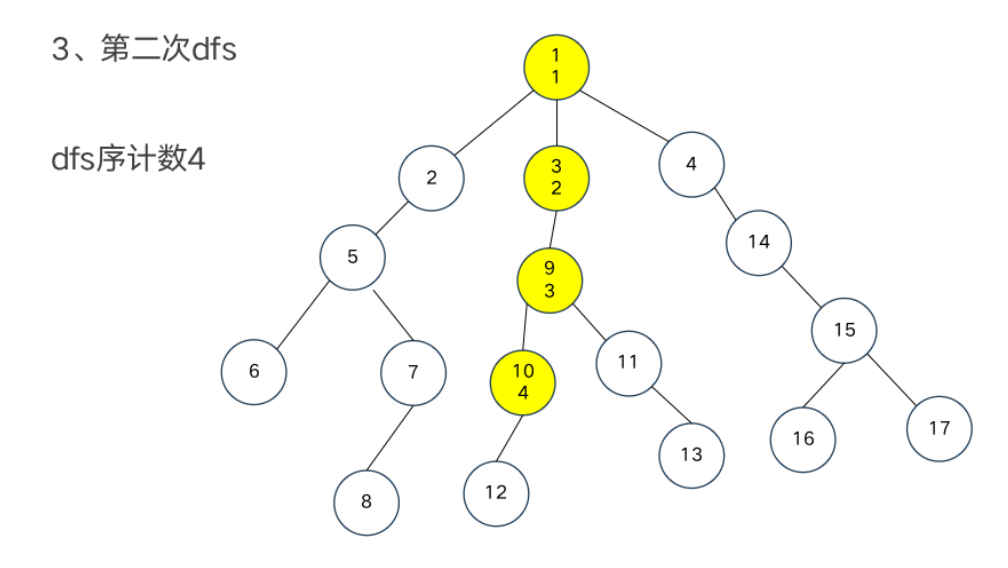
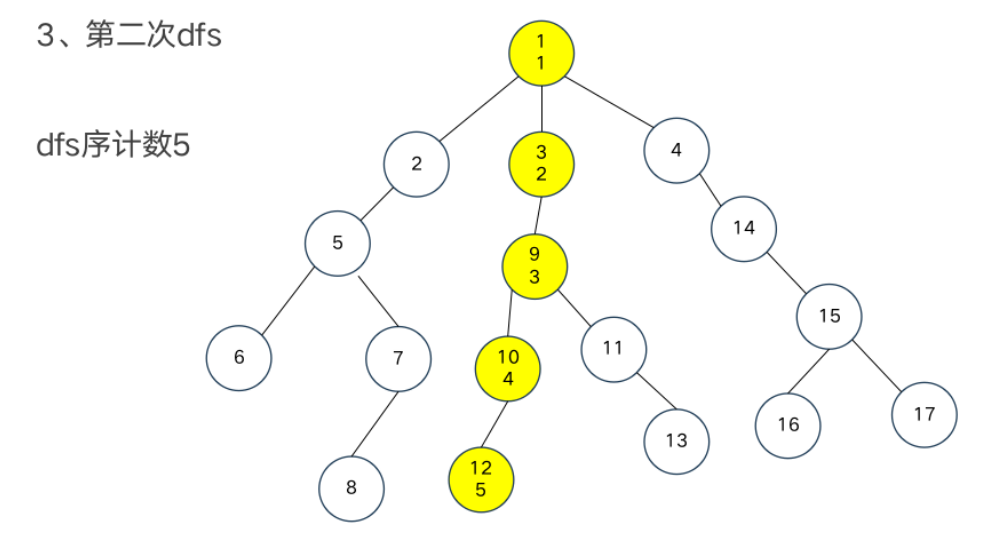
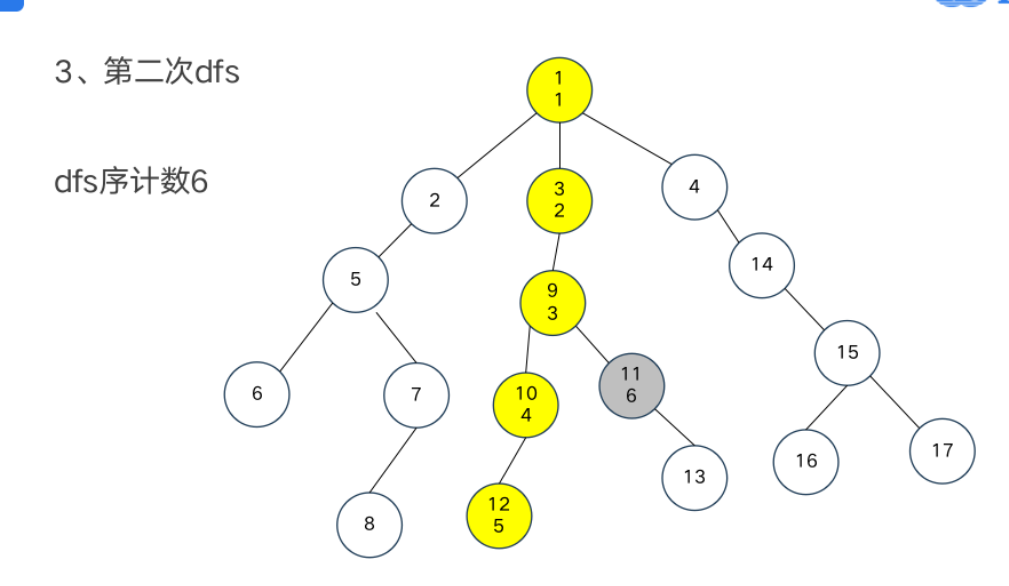
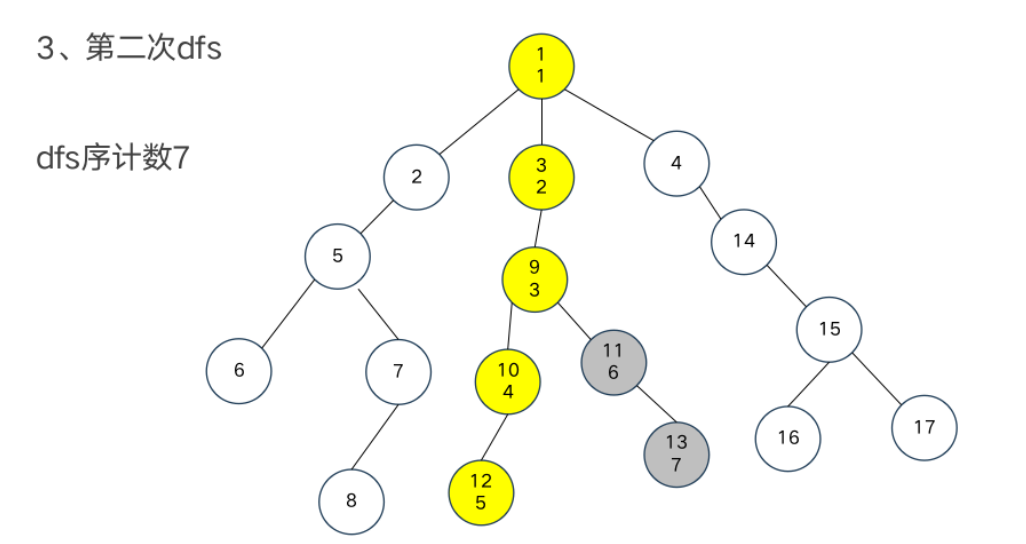
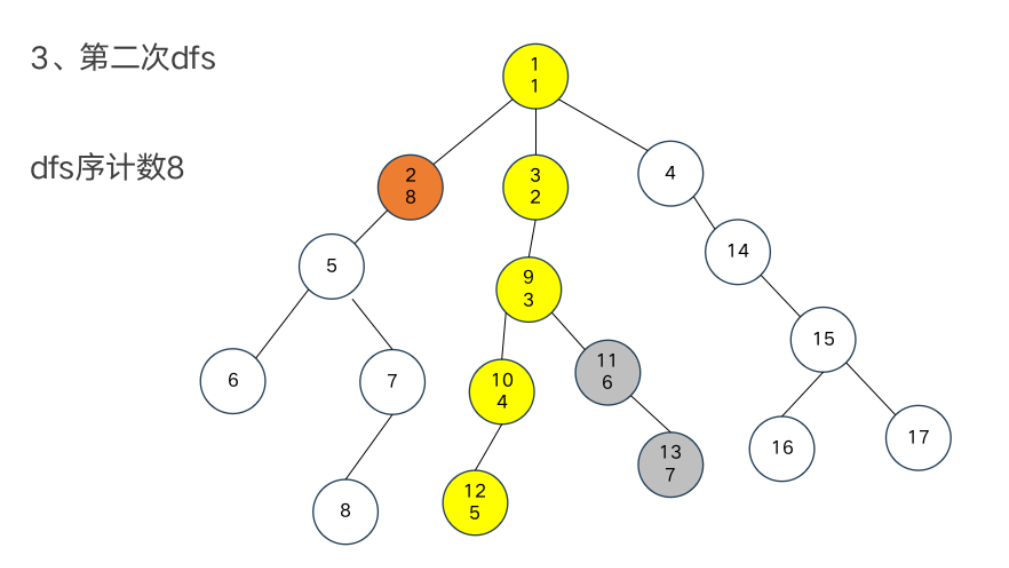
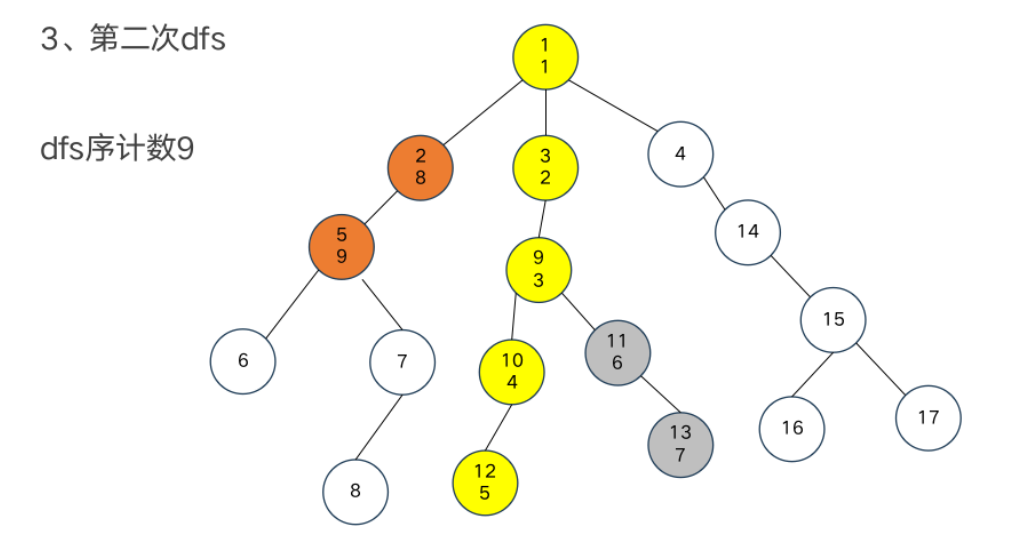
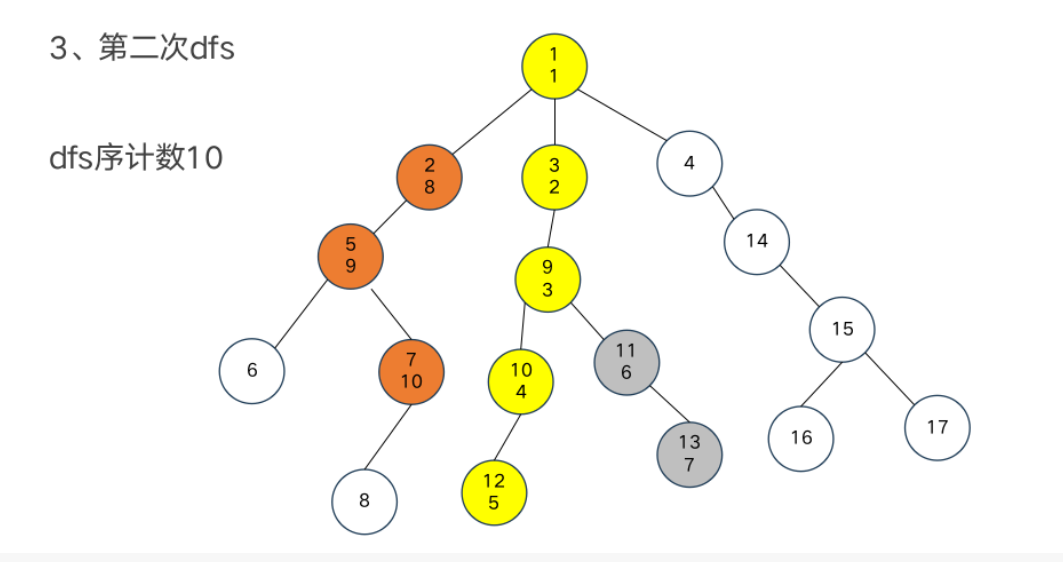
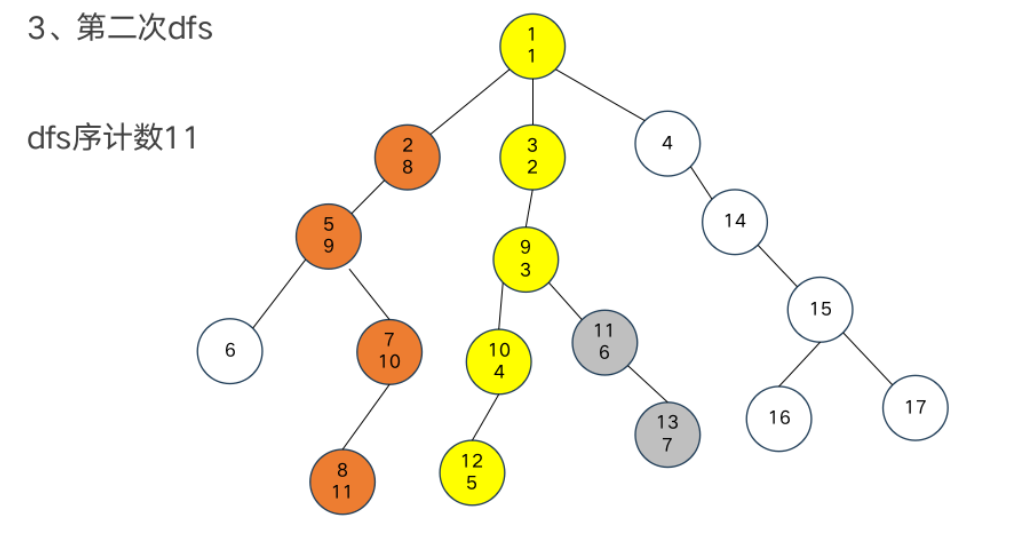
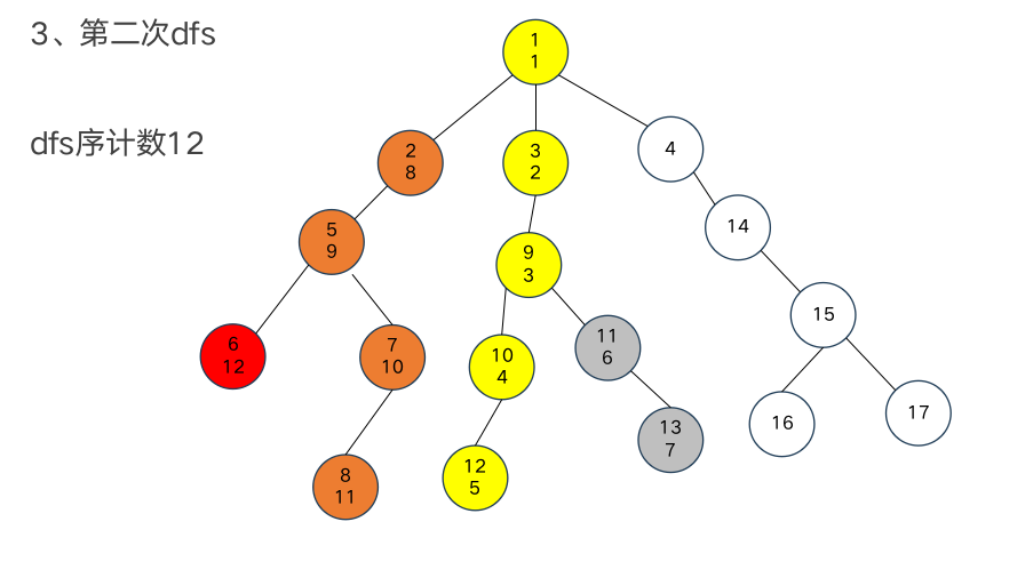
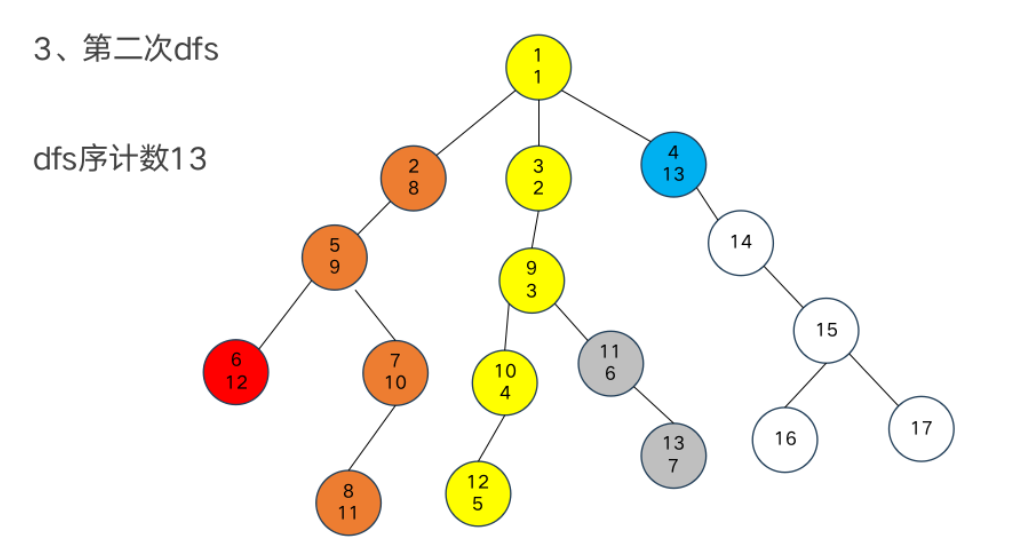
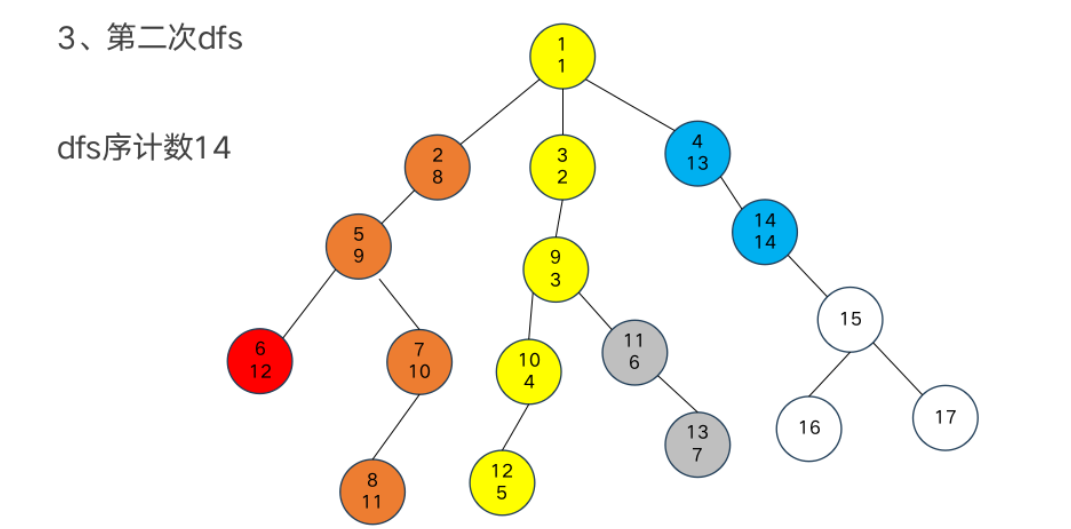
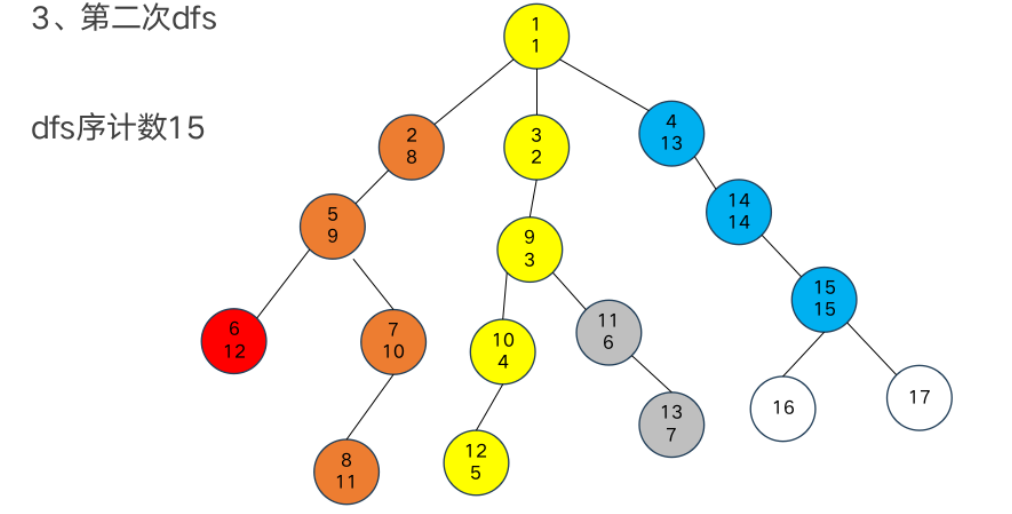
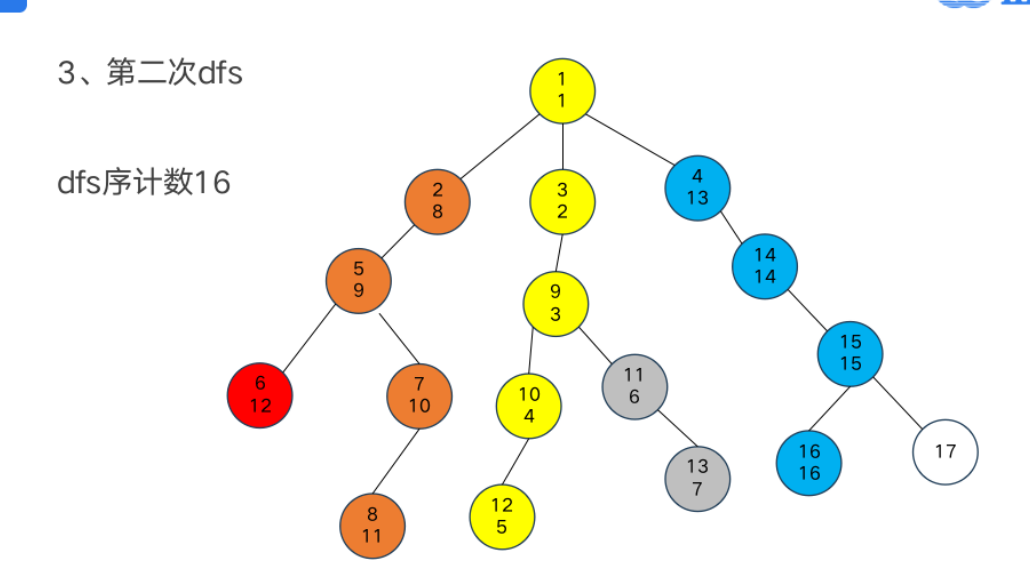
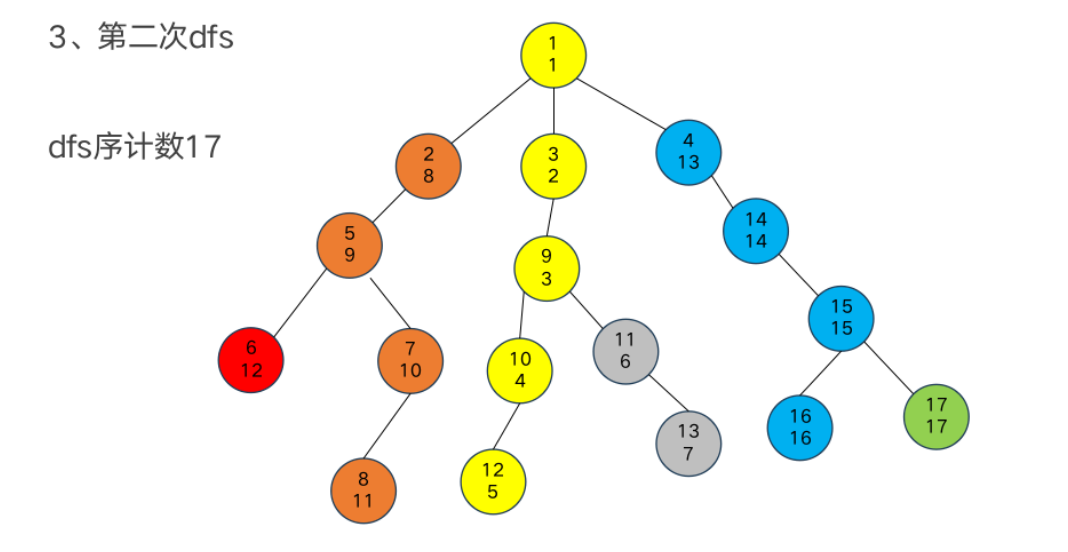
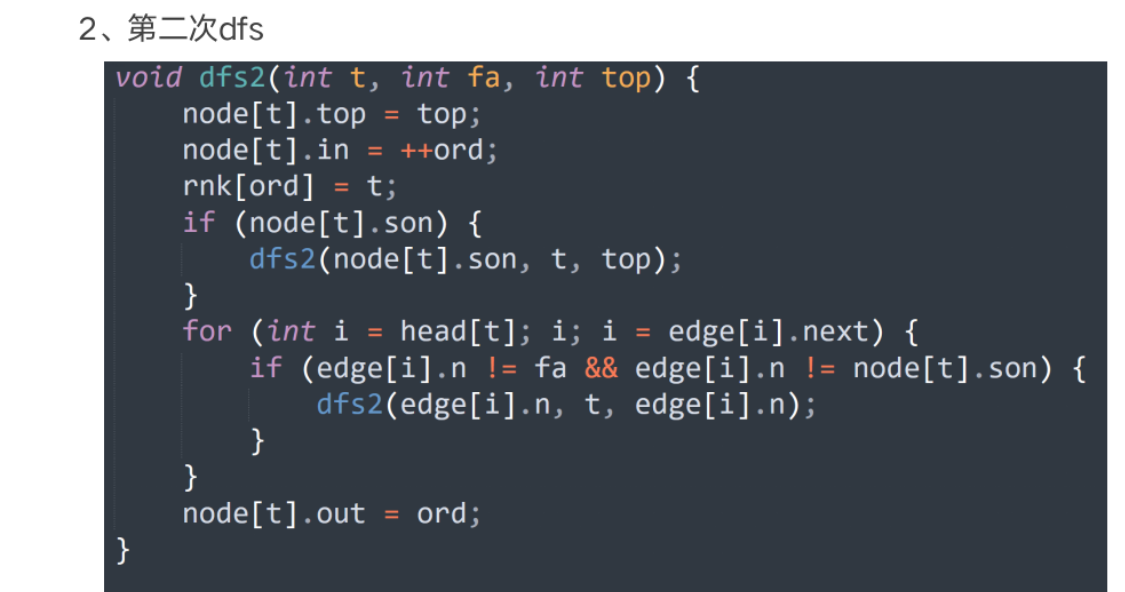
树链部分的性质

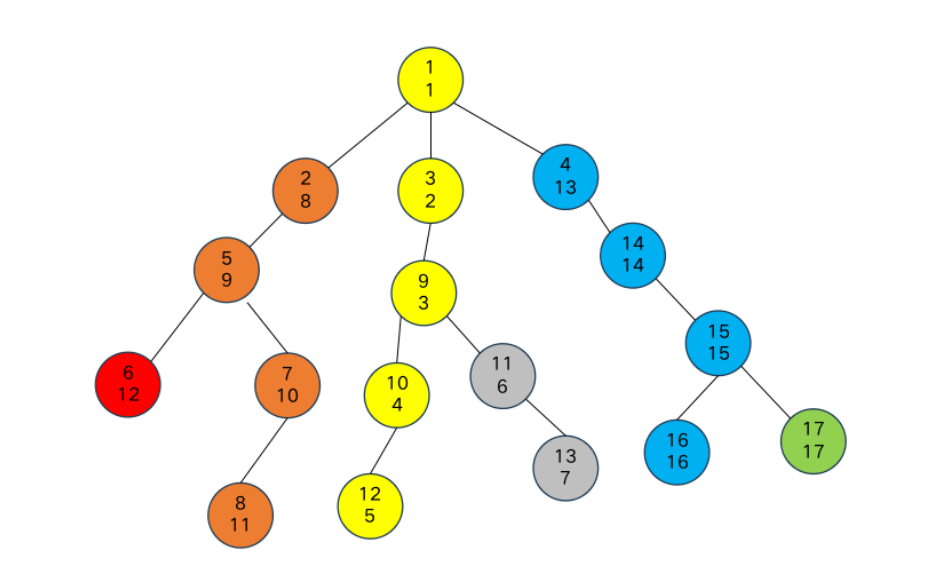



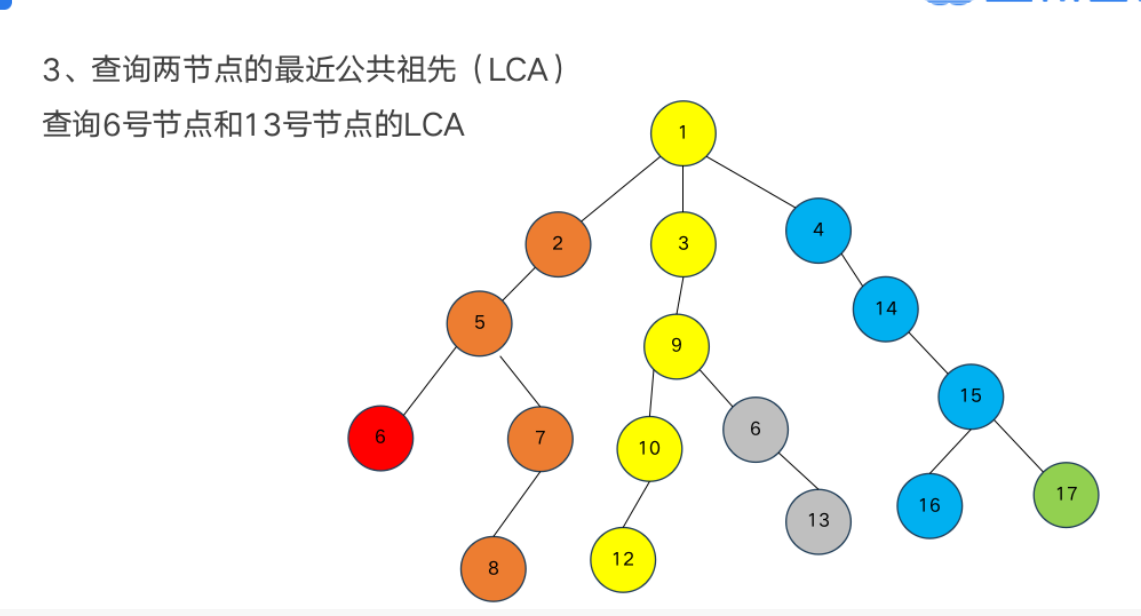
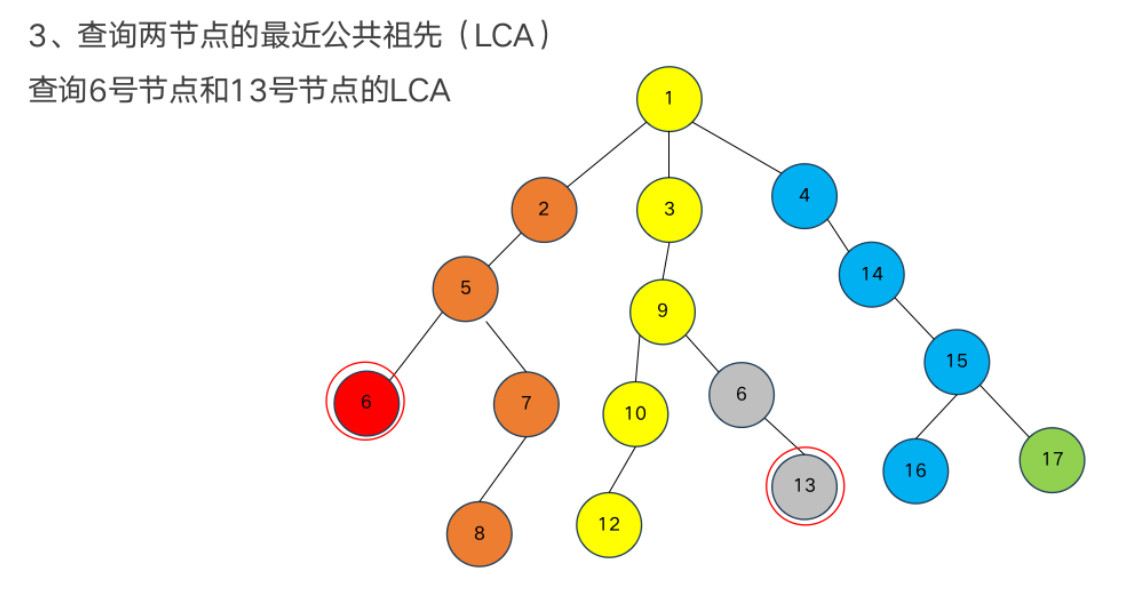


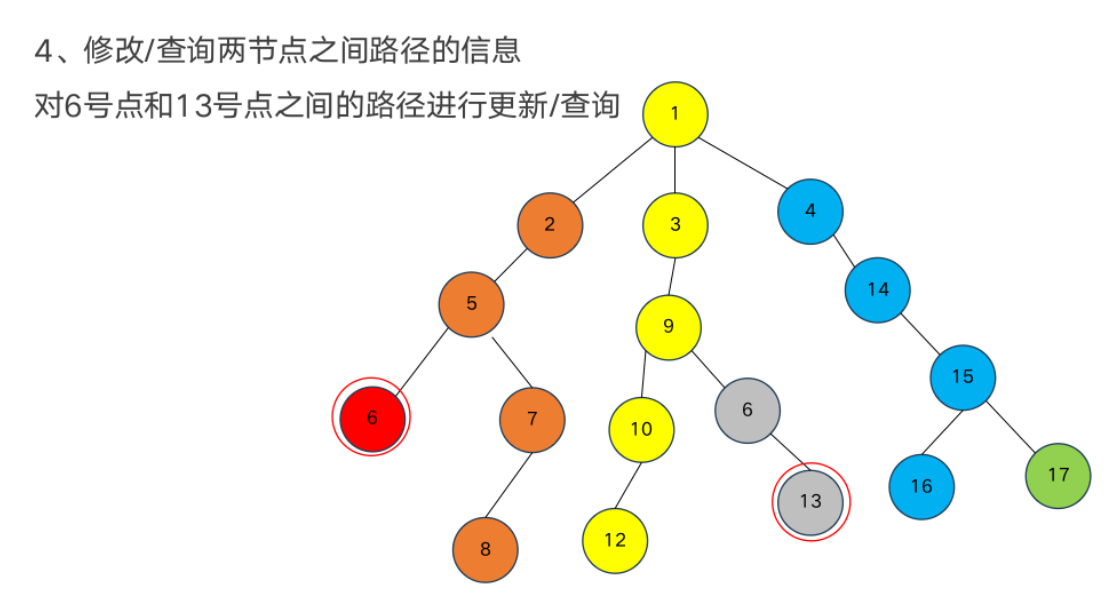
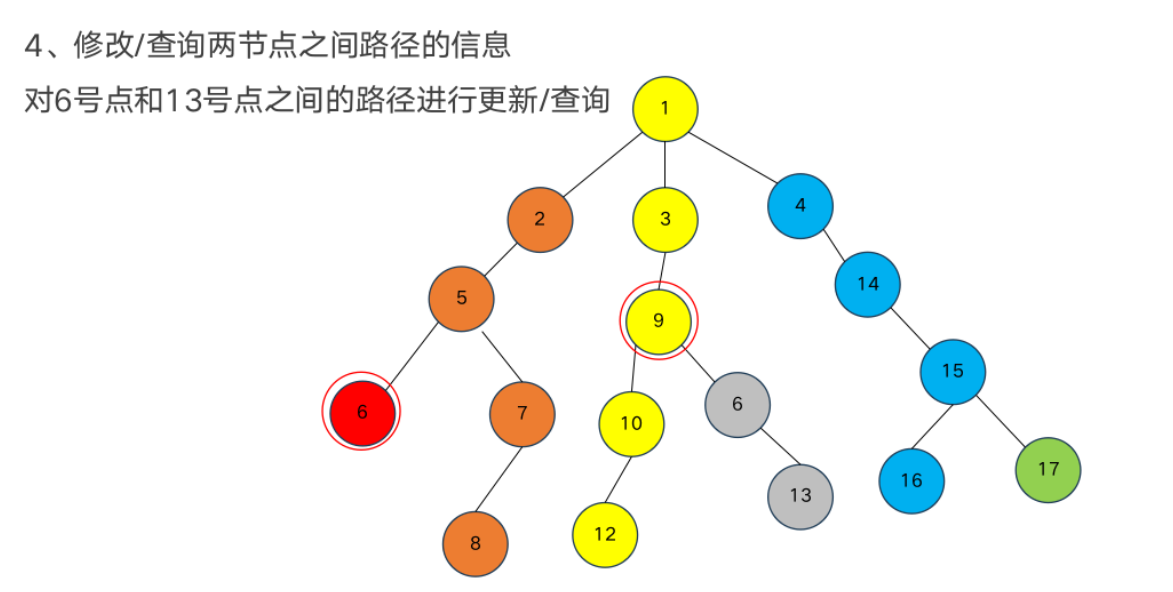
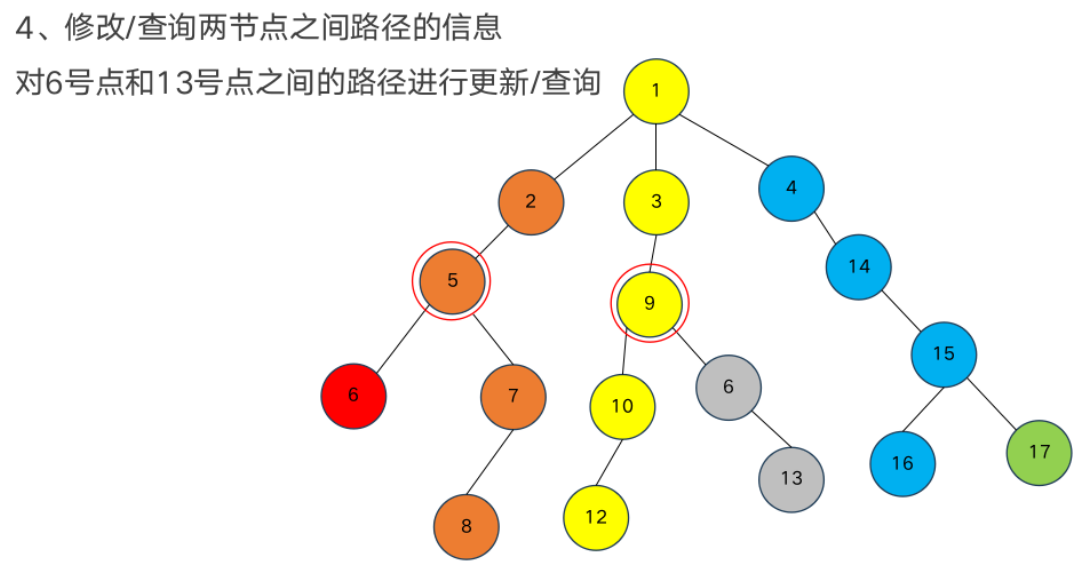
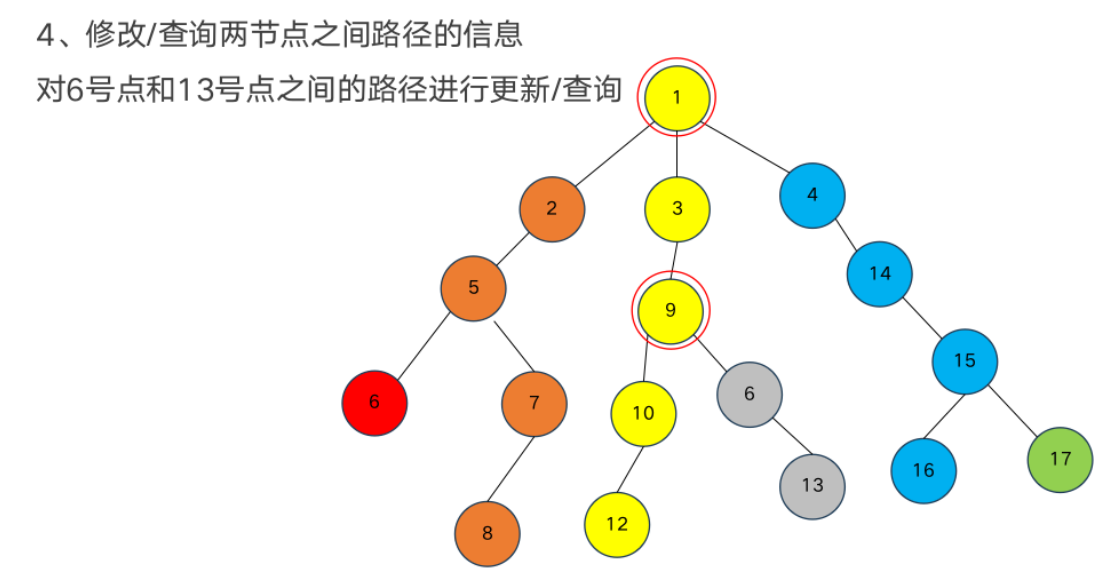


树形数据结构
树状数组基础
lowbit操作

树状数组
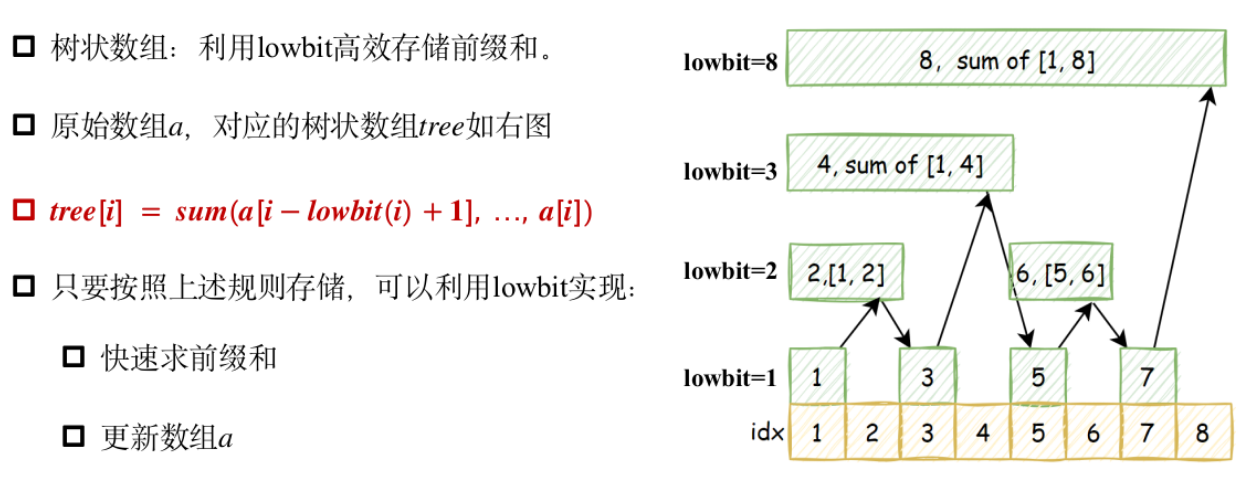
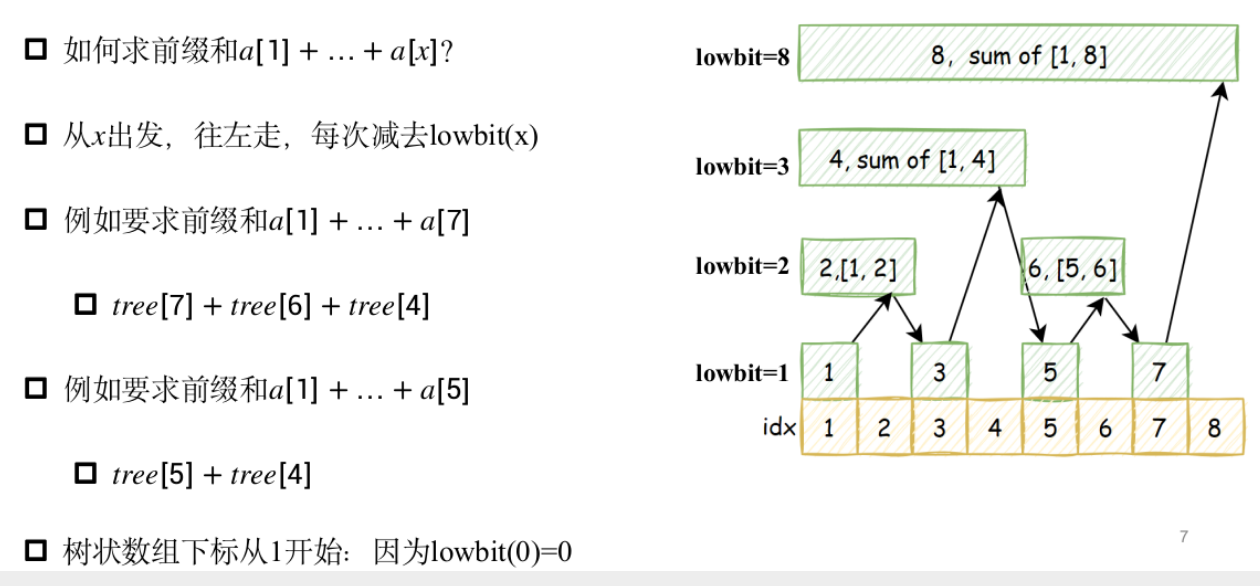
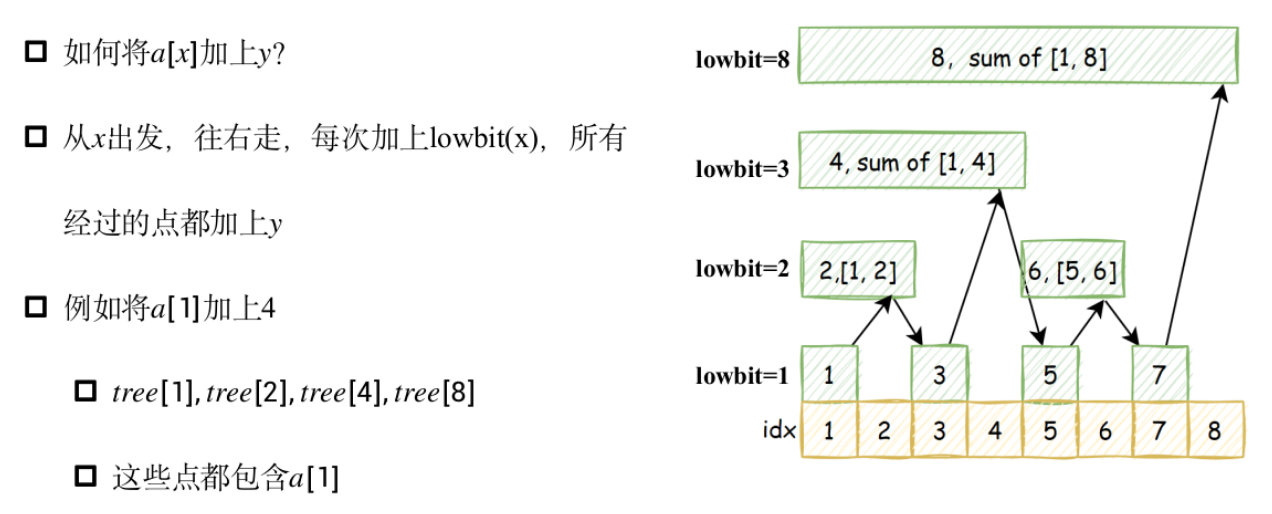
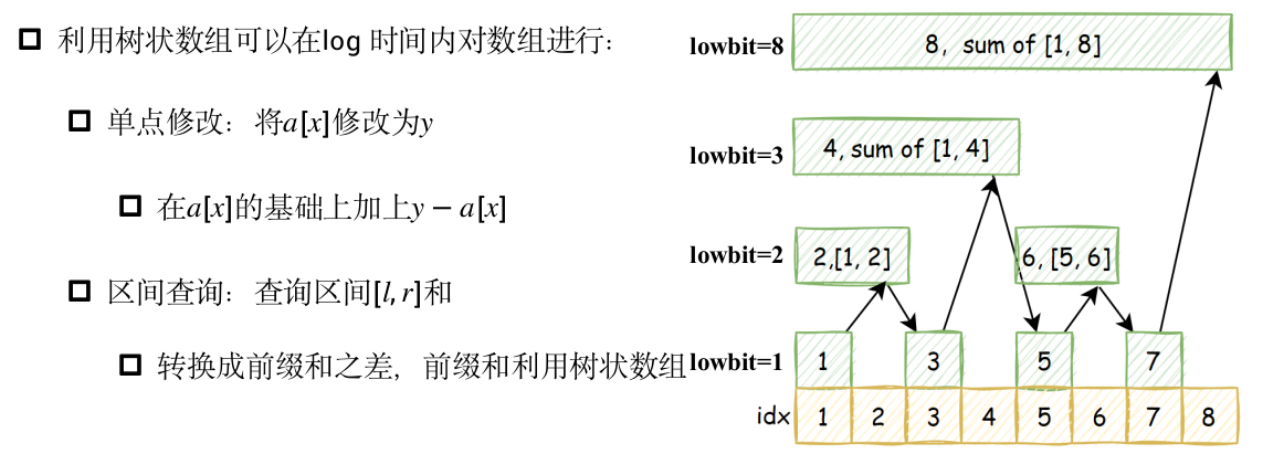
模板题——单点修改,区间查询
1 | |
1 | |

树状数组
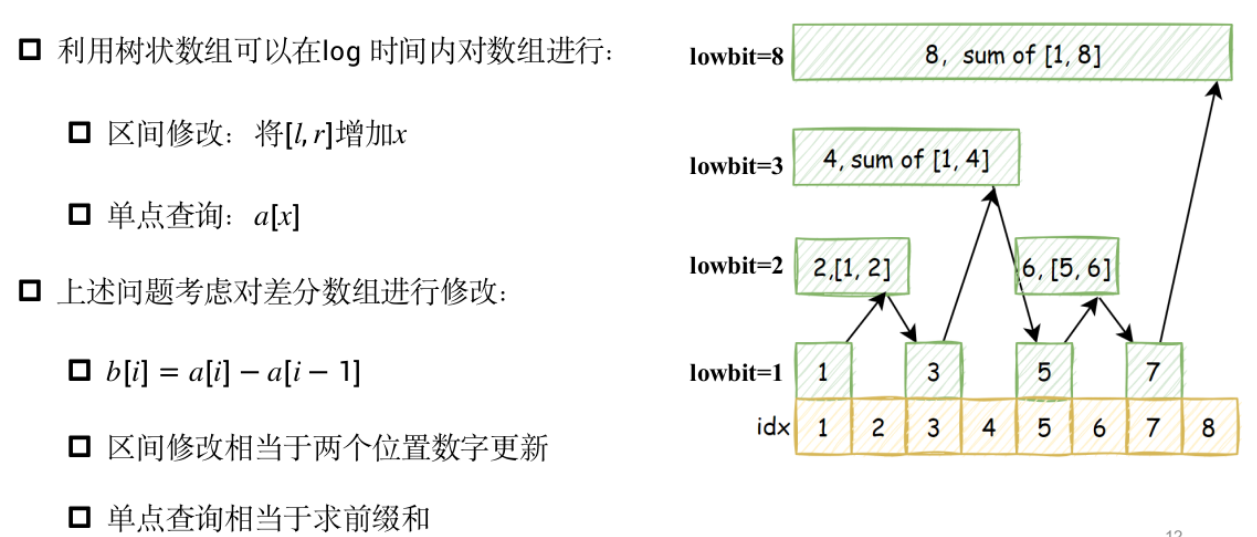
模板题——殷老师排队
1 | |
二维树状数组



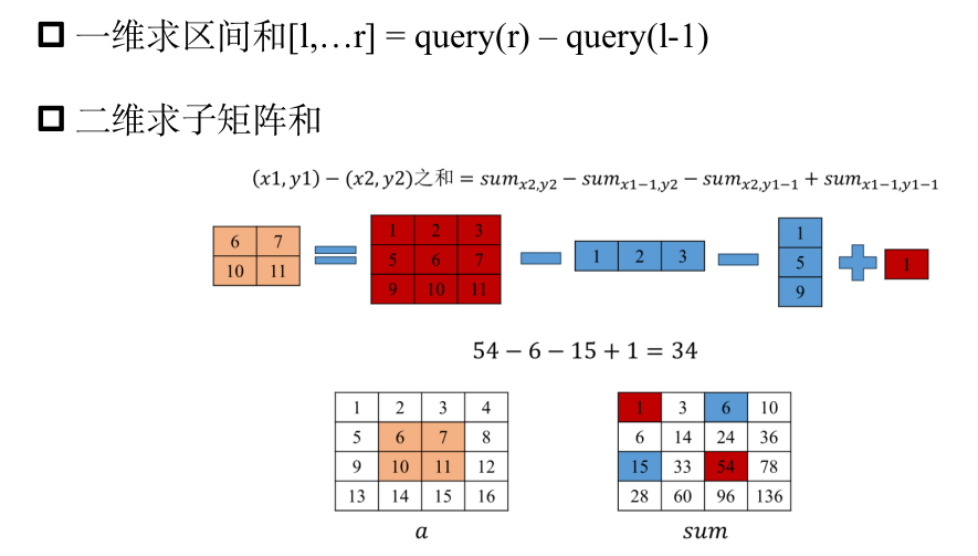

模板题——

树状数组上二分








模板题——
1 | |
线段树-动态开点




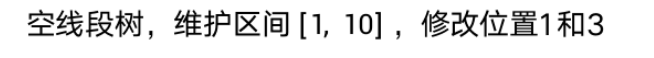
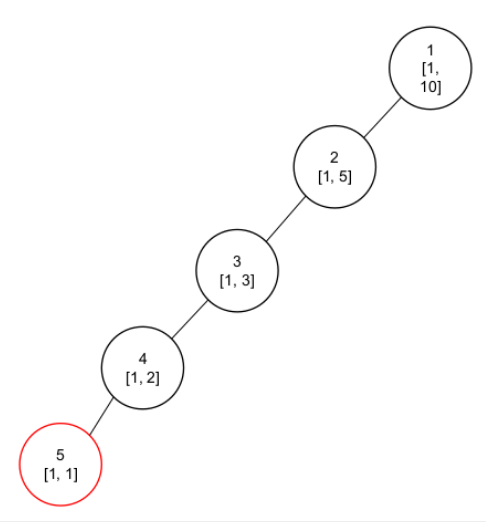
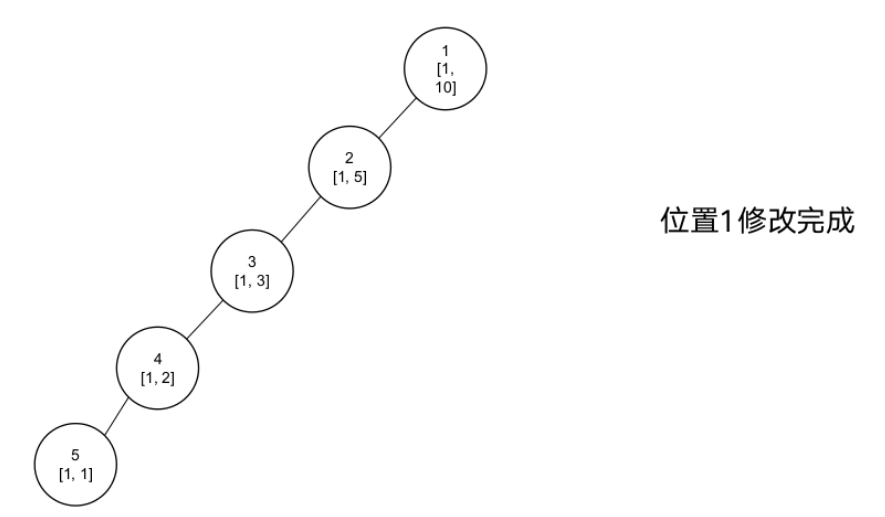
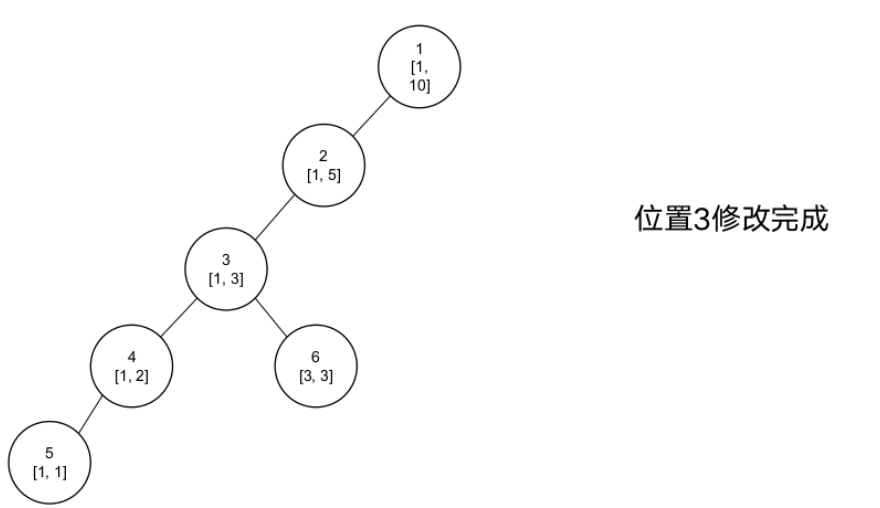

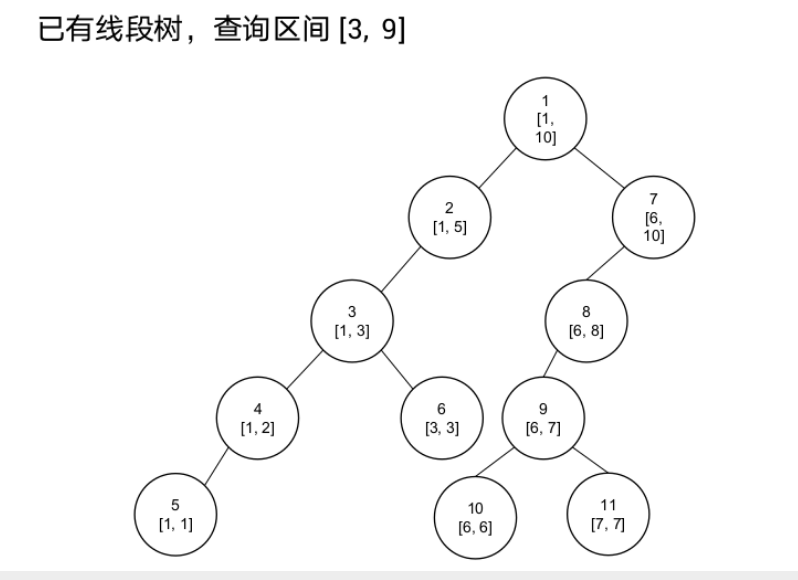
例题

1 | |
线段树-标记永久化


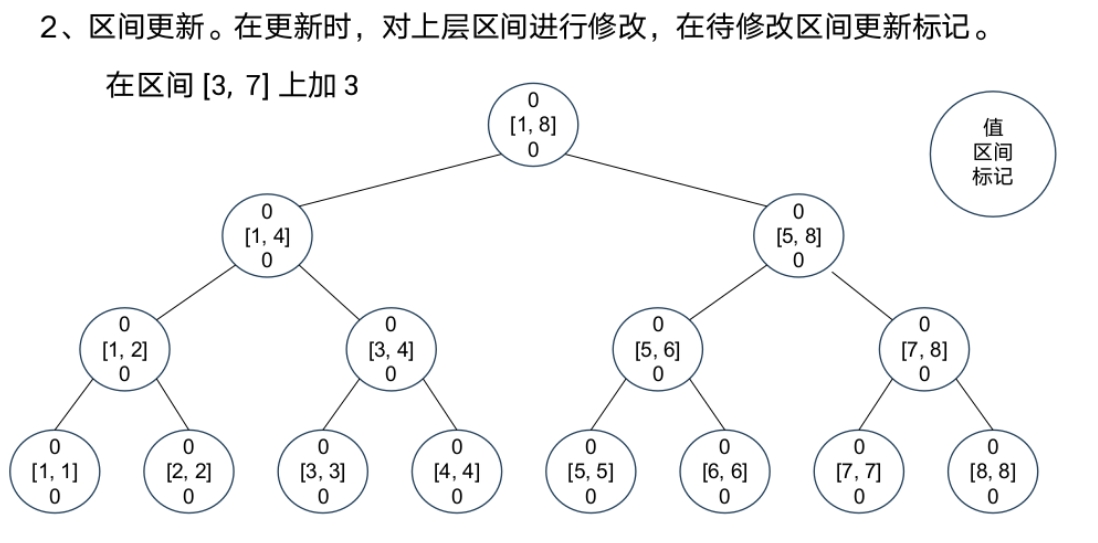

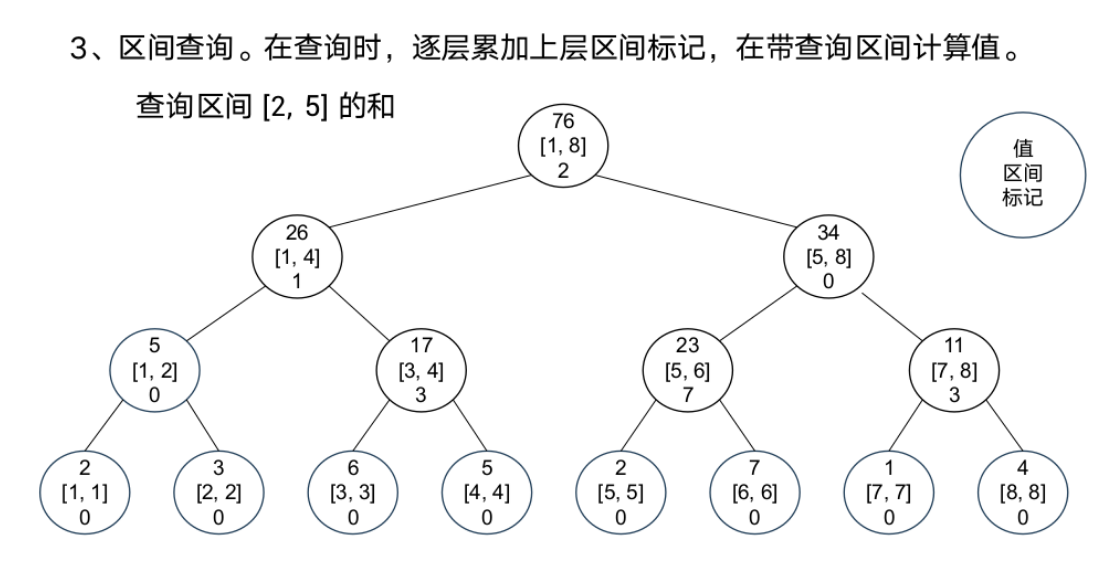
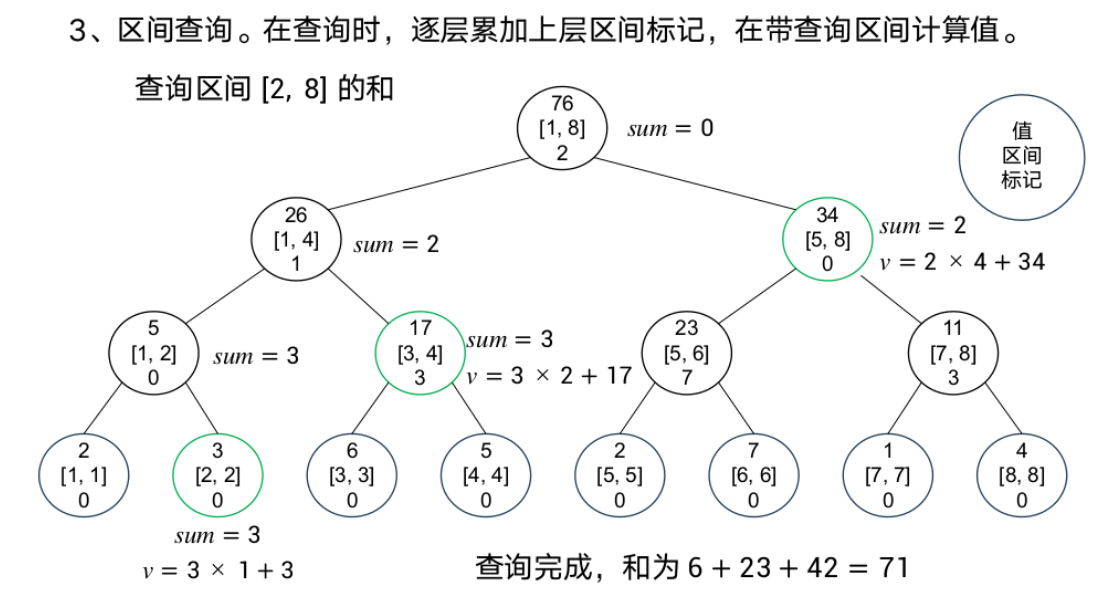



案例
1 | |
线段树维护矩阵








1 | |
线段树维护哈希


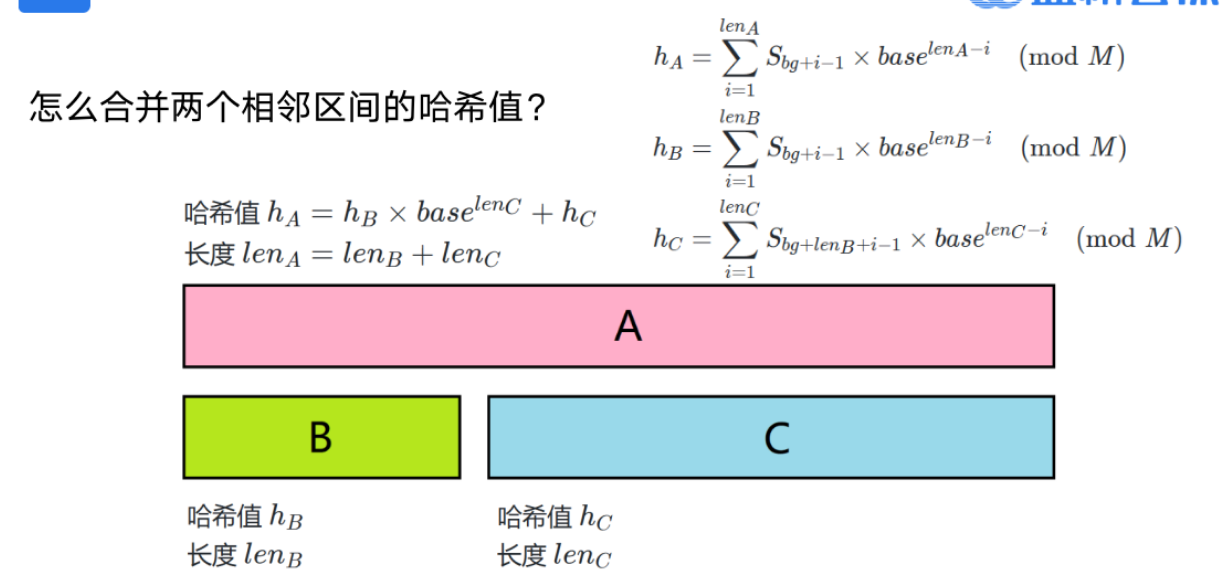



1 | |
可持久化线段树
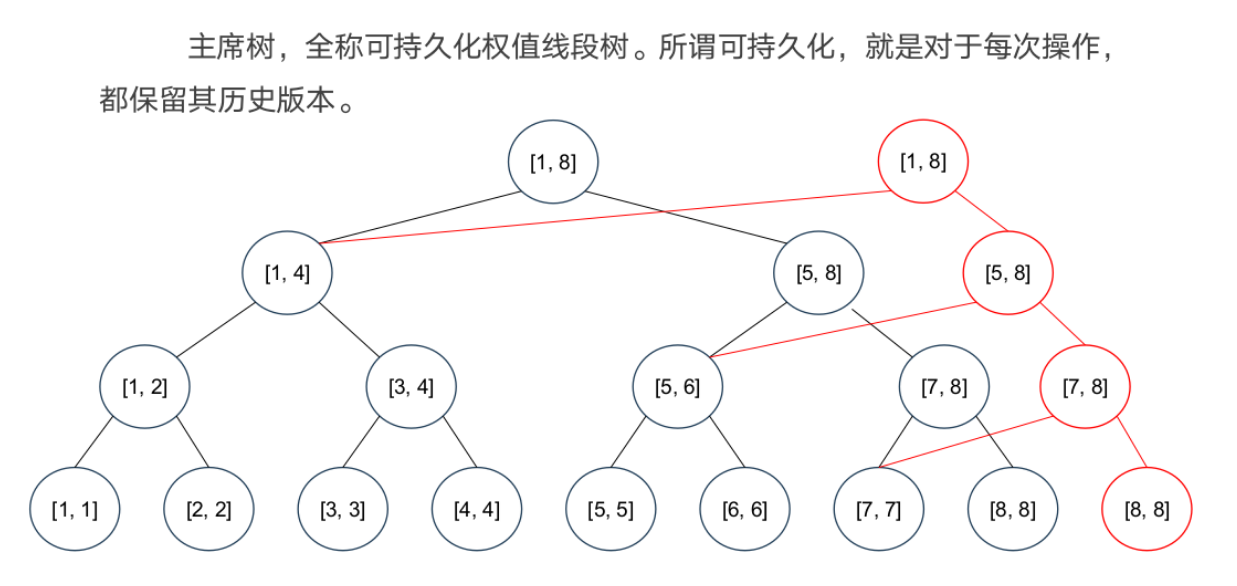



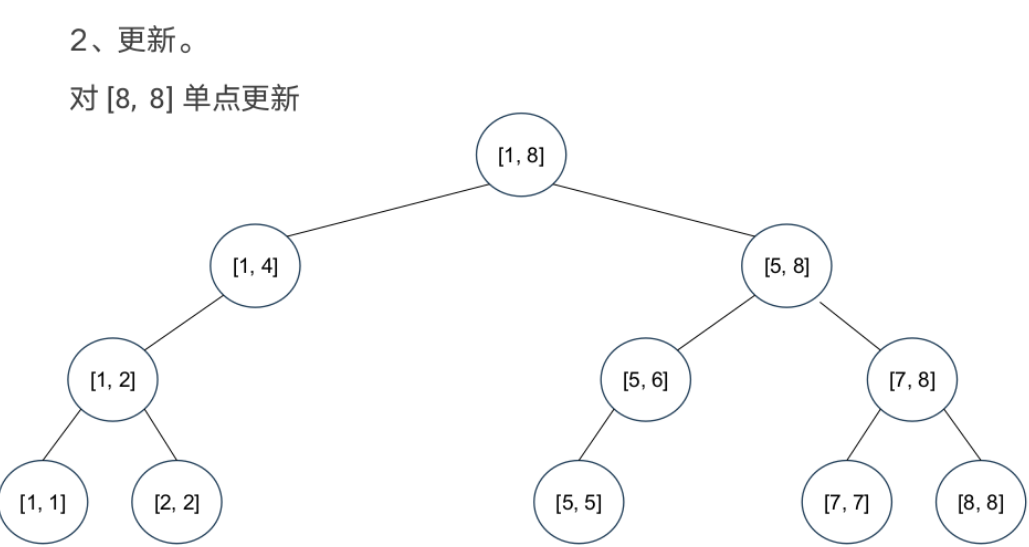


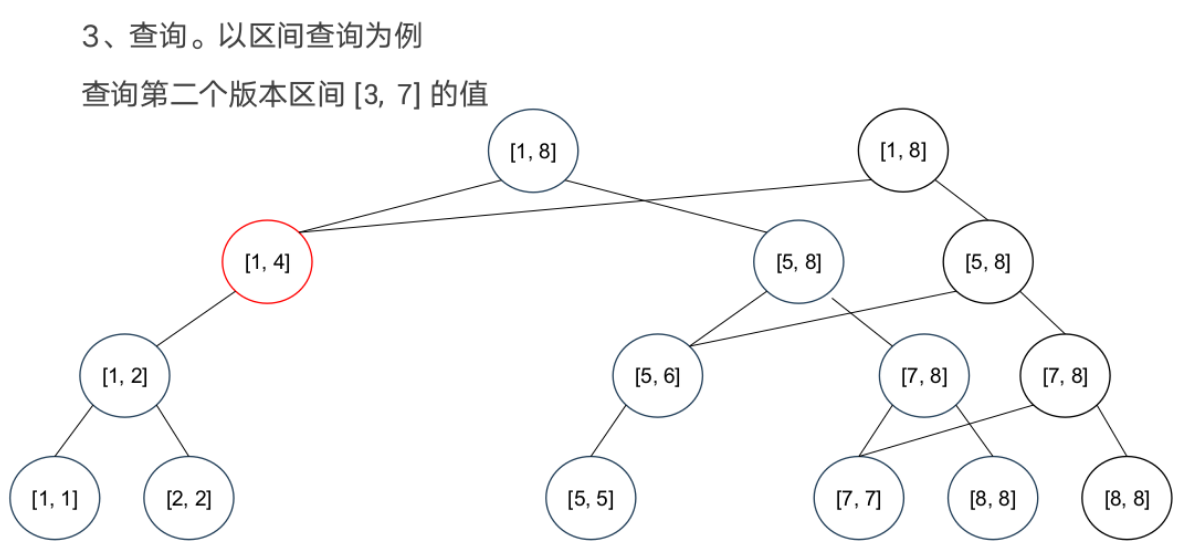
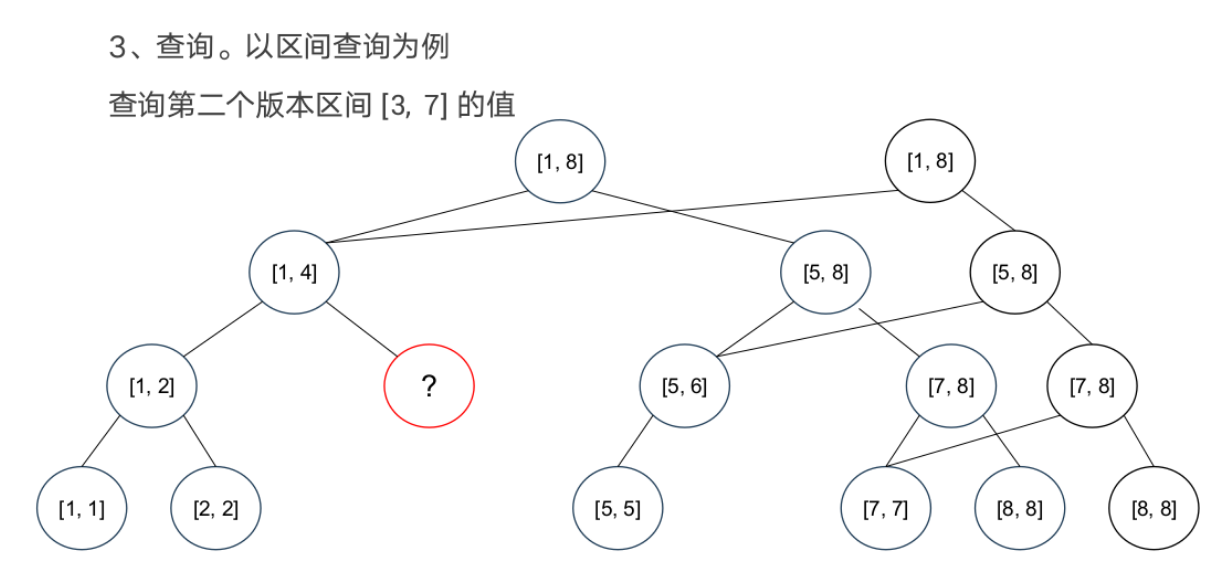

可持久化线段树
1 | |
模板题——区间第k小
1 | |
扫描线与二维数点
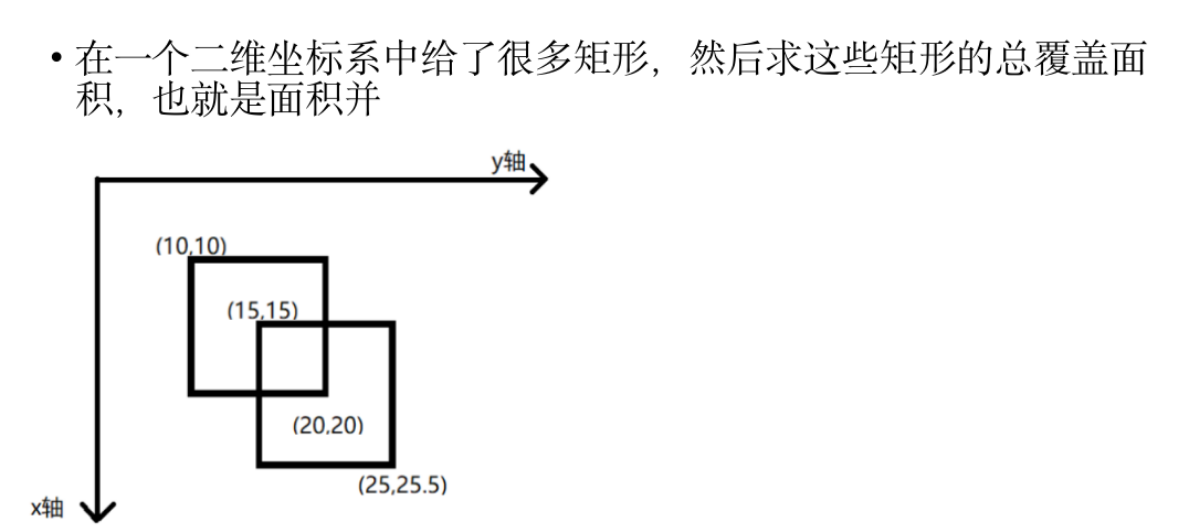




二维数点



1 | |
平衡树-Splay

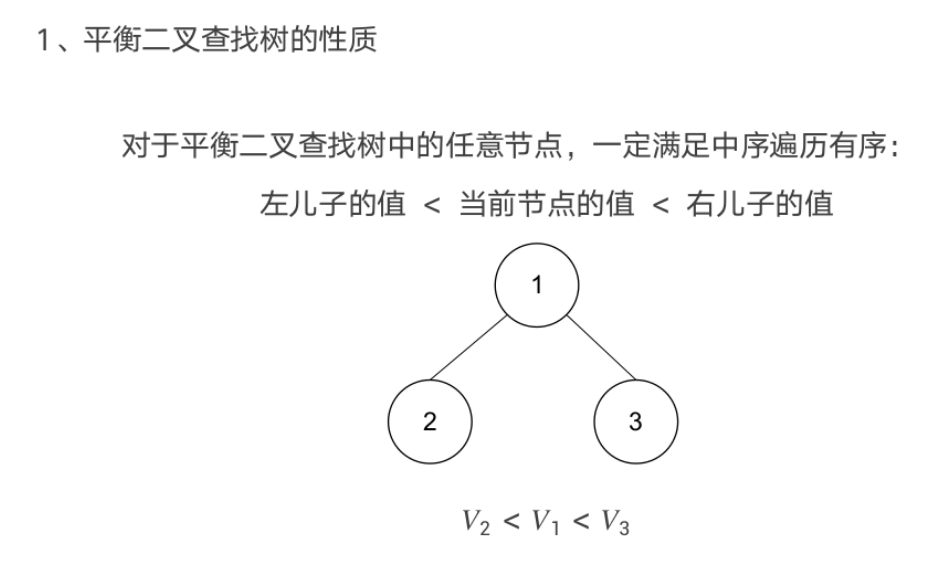


平衡树-FHQ_Treap
无旋Treap

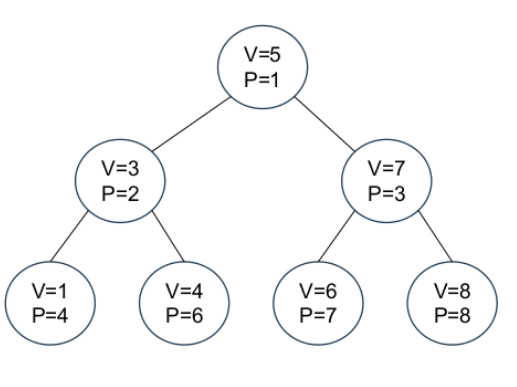

无旋Treap的结构
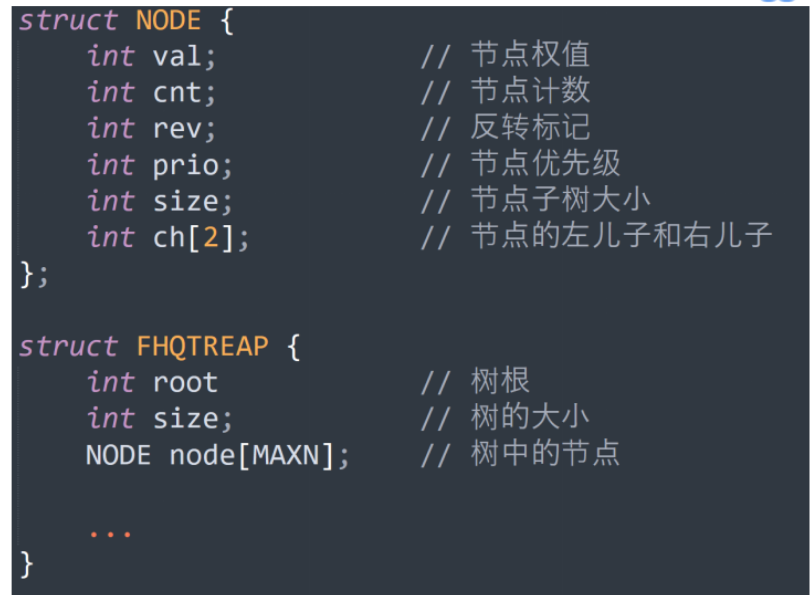
基本操作
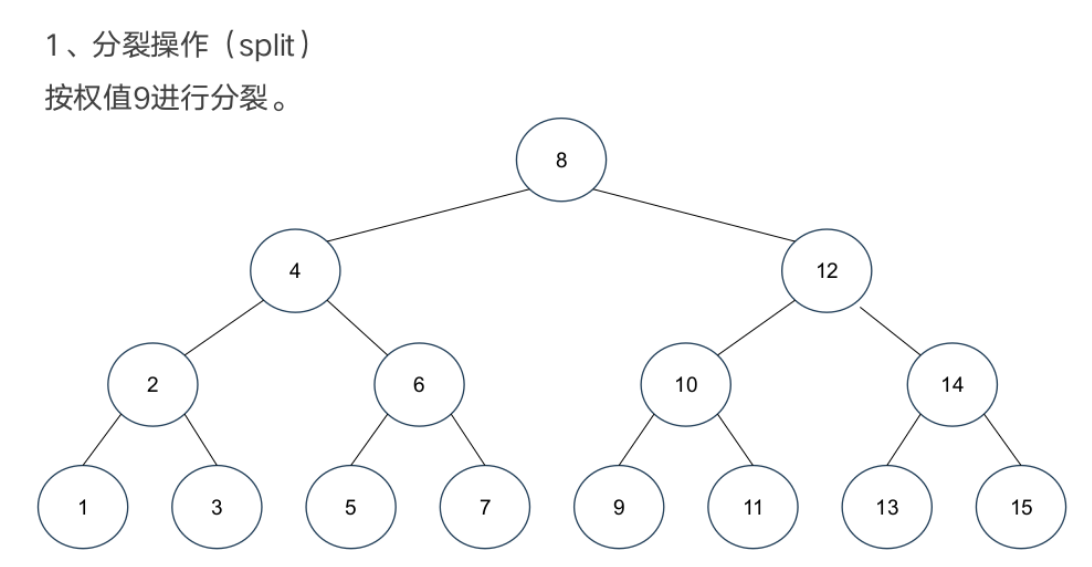
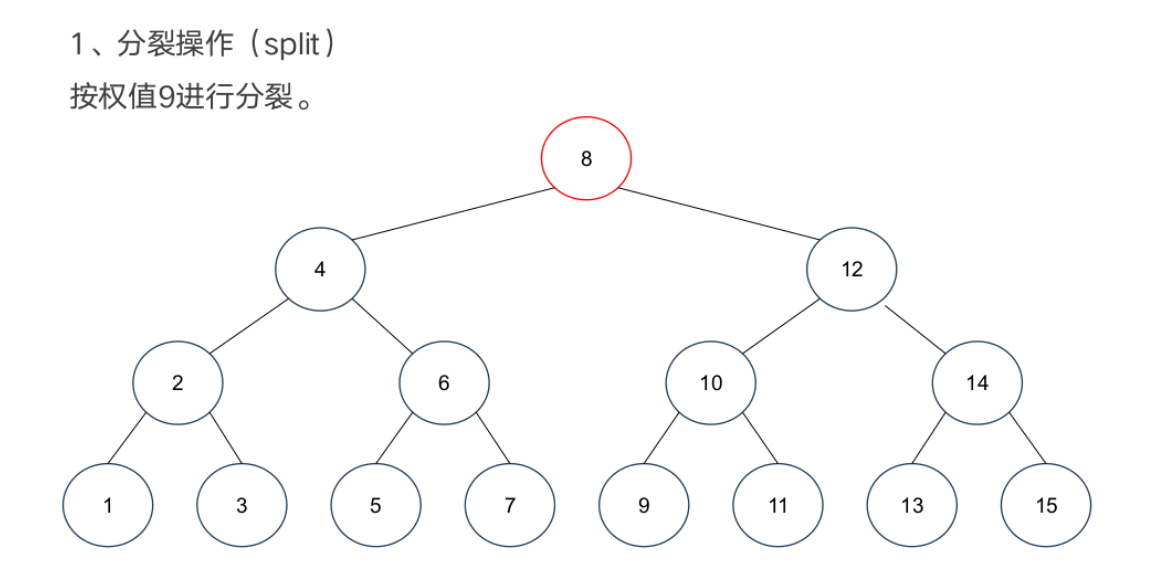
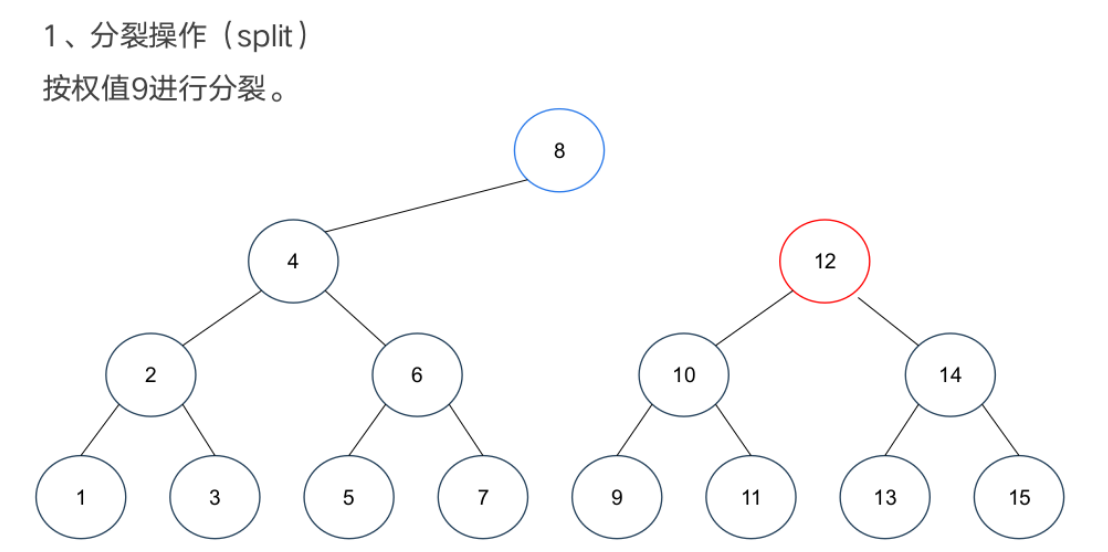
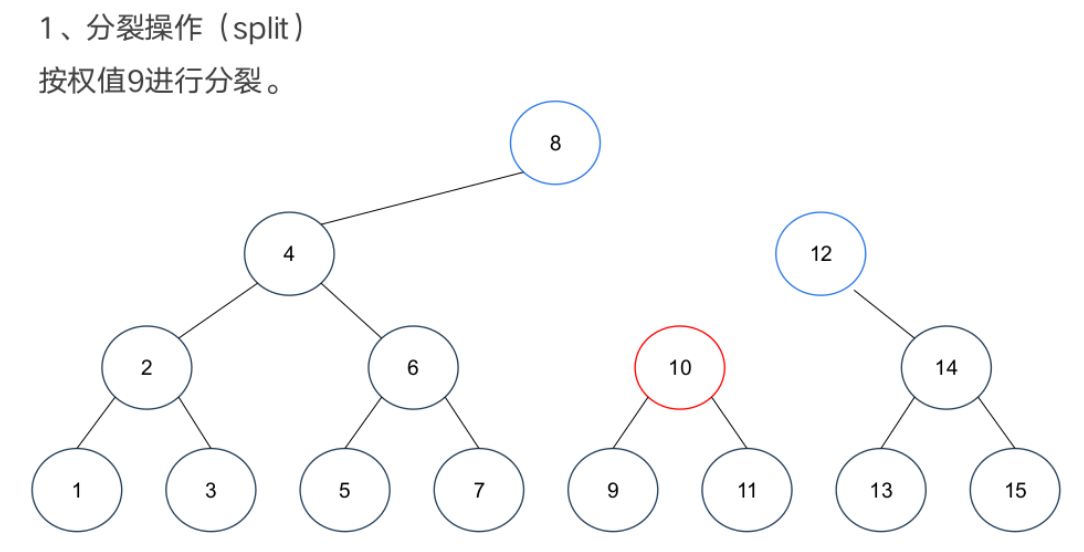
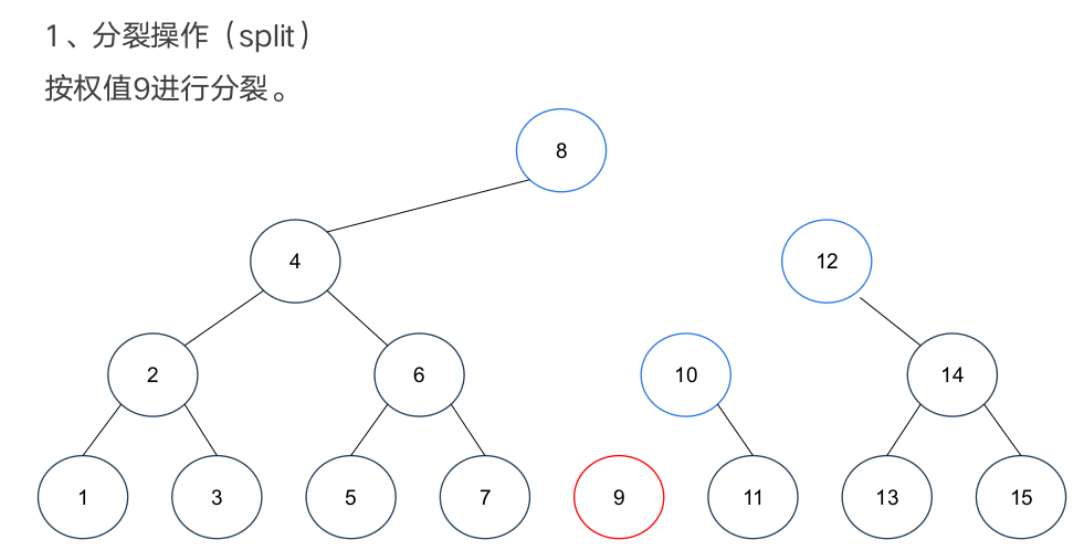
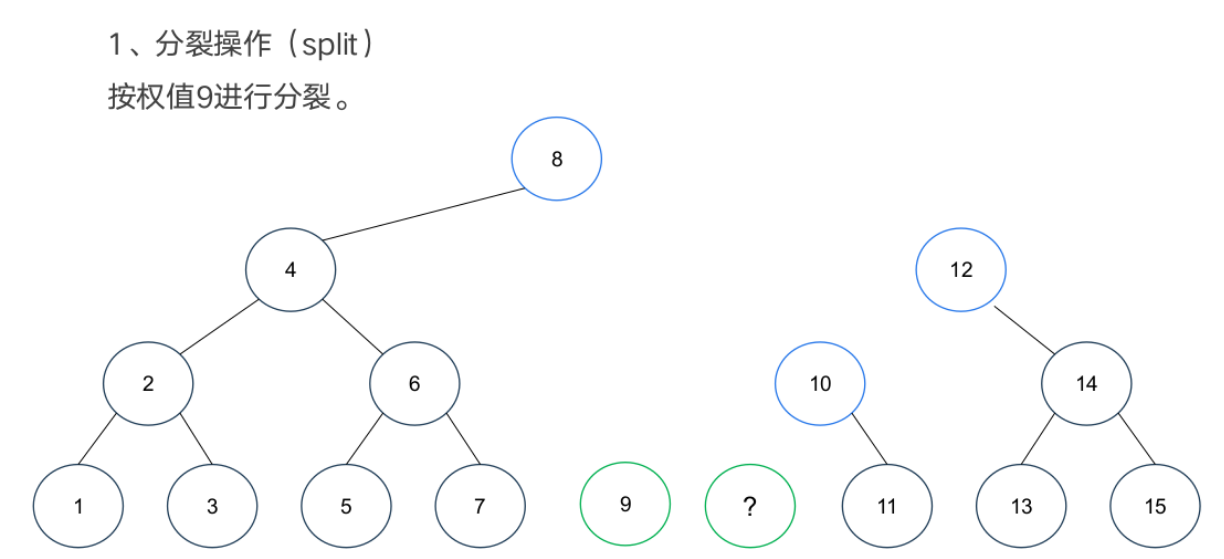
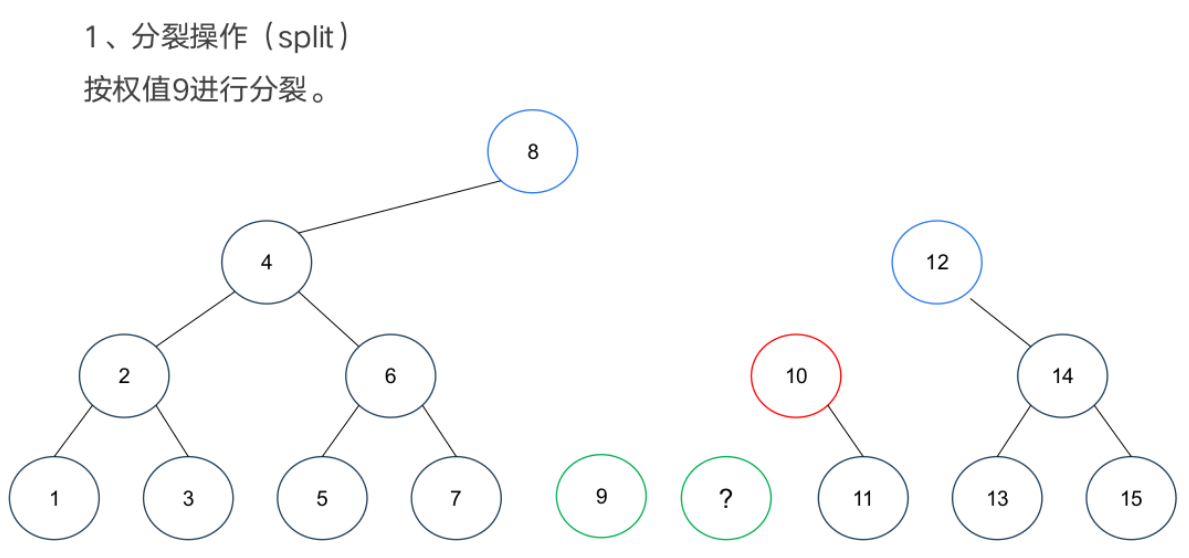
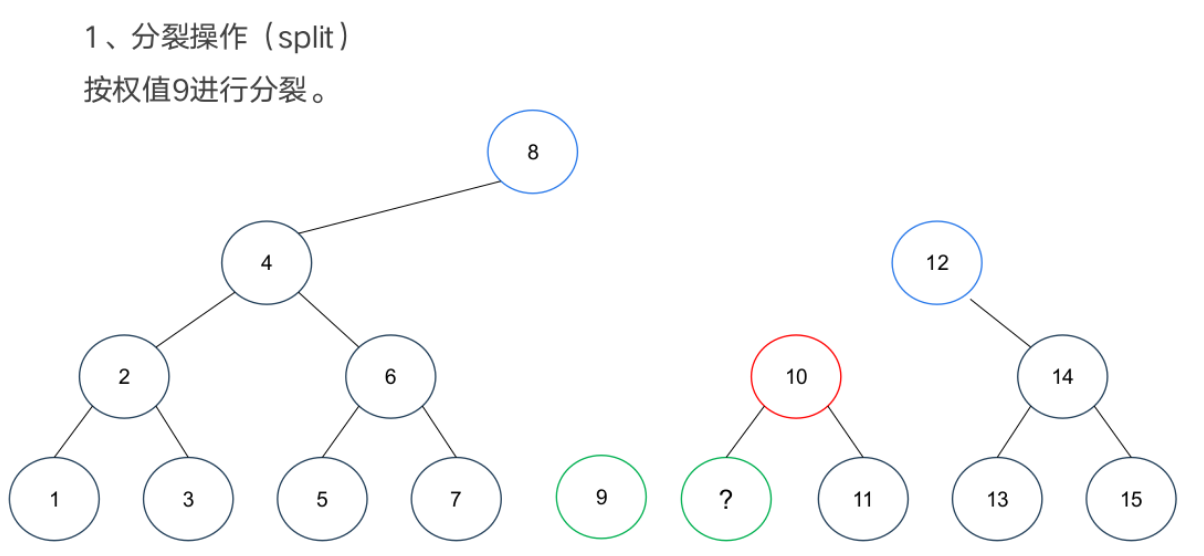
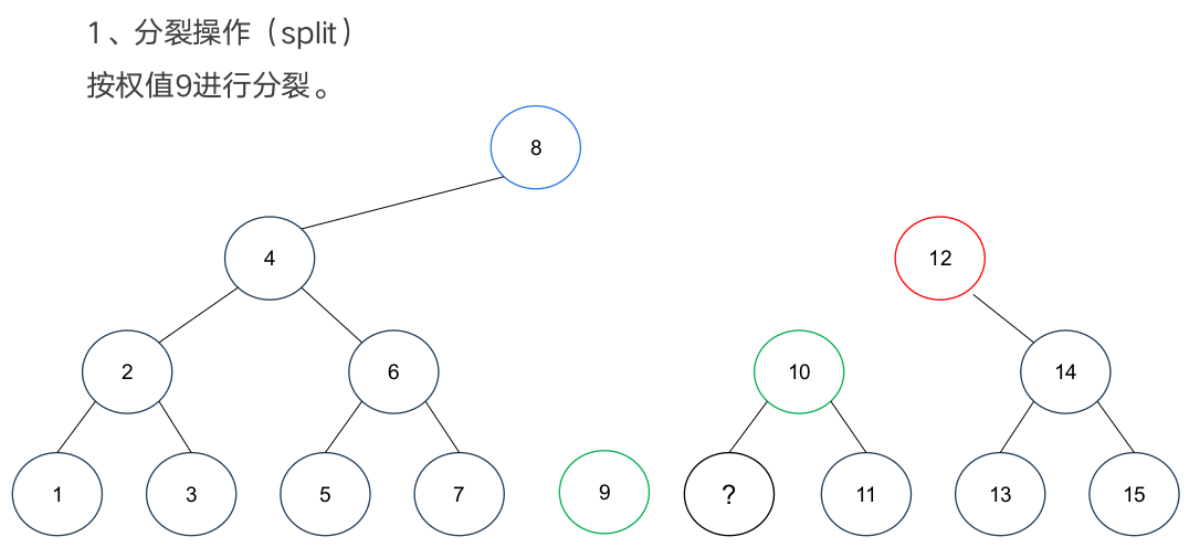
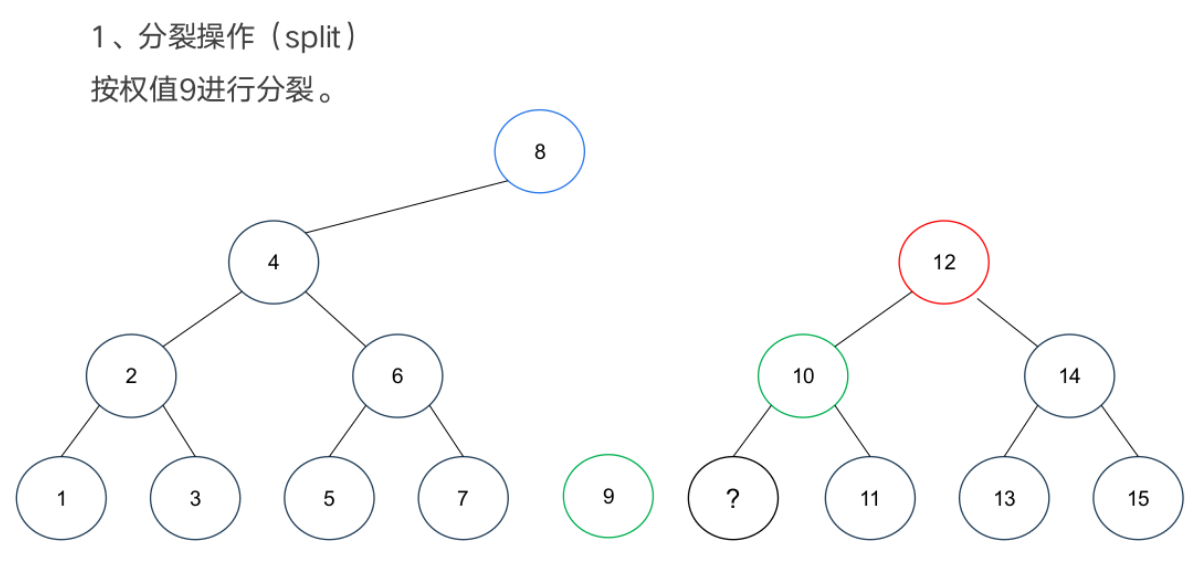
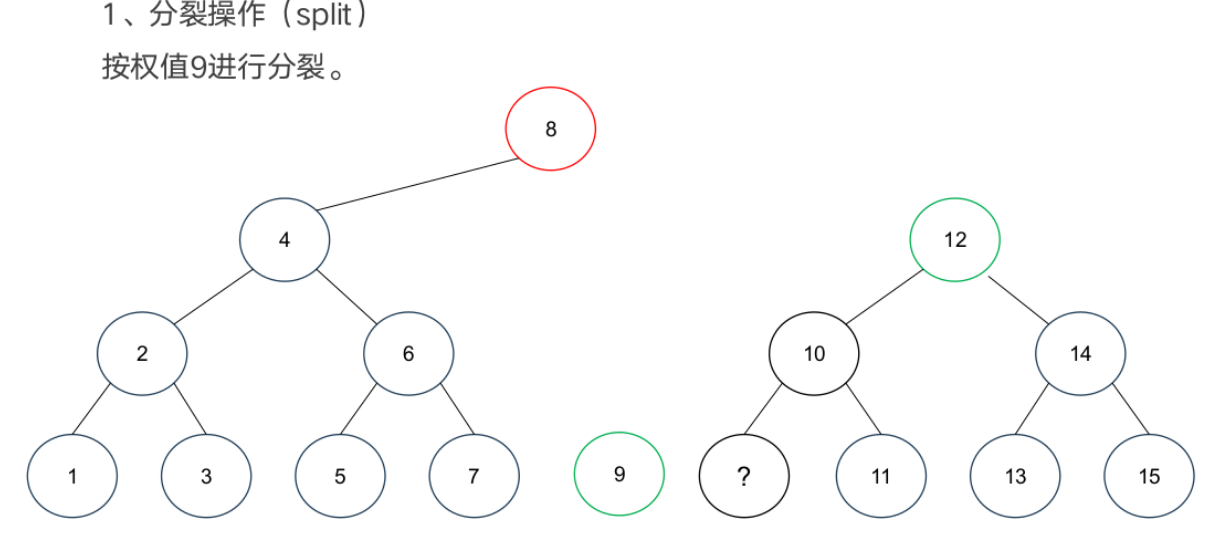
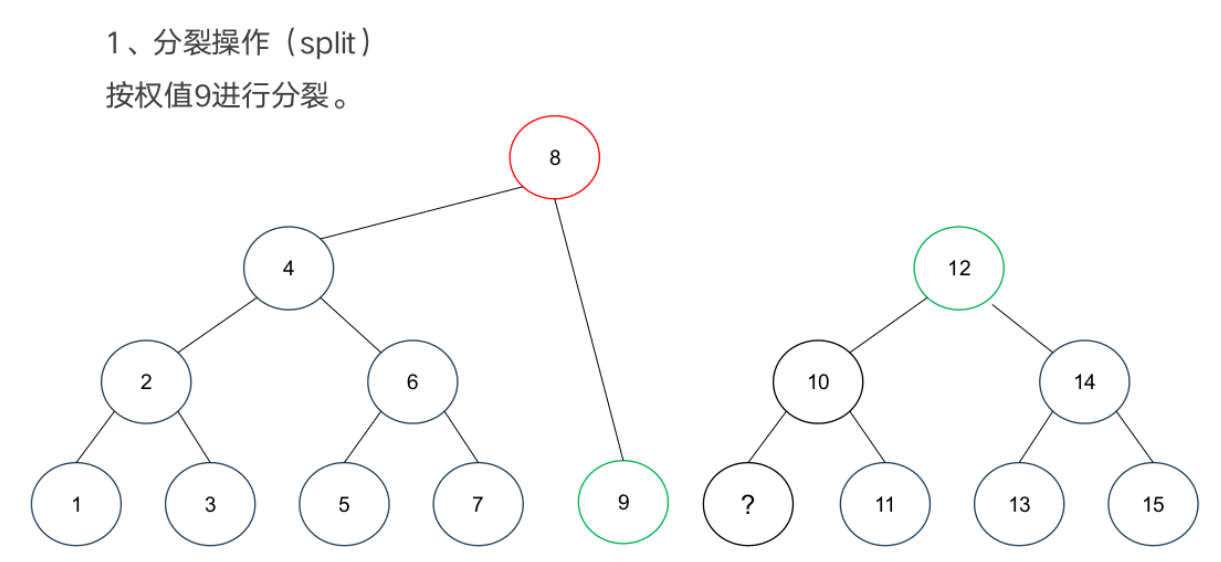
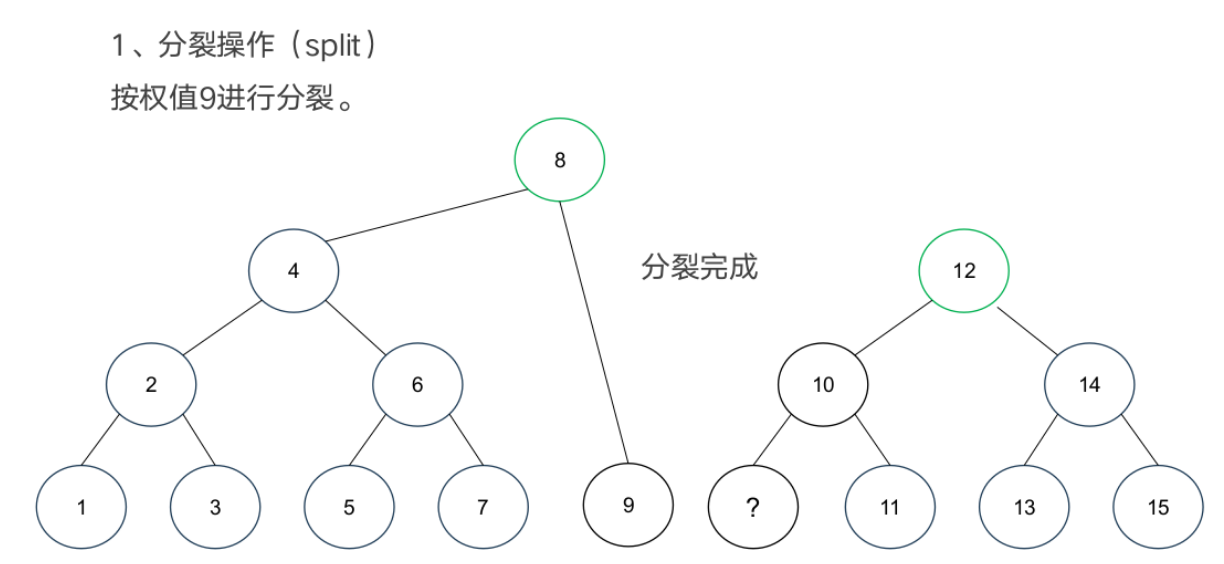
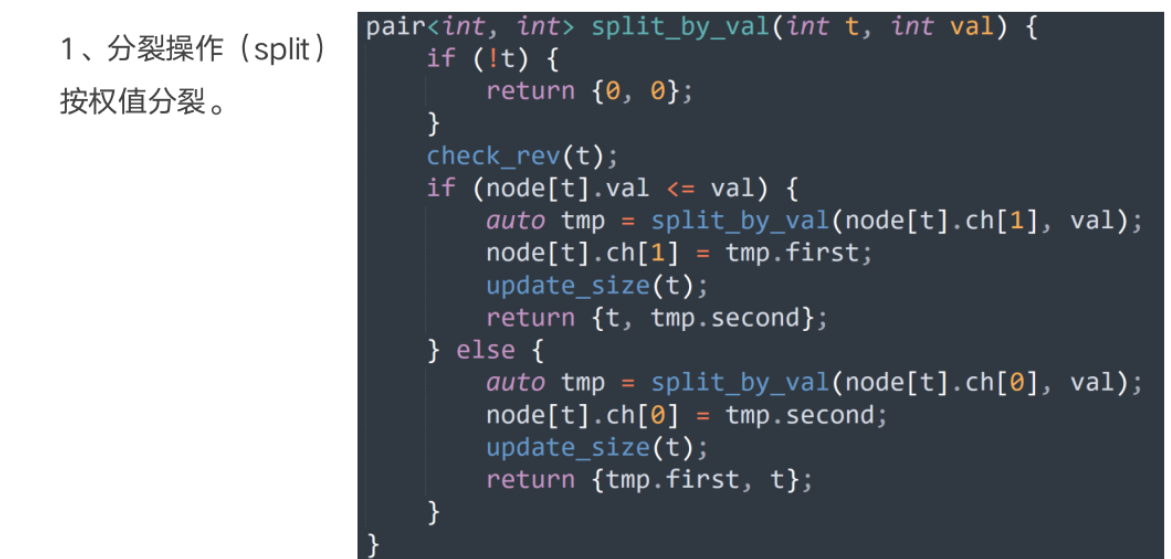

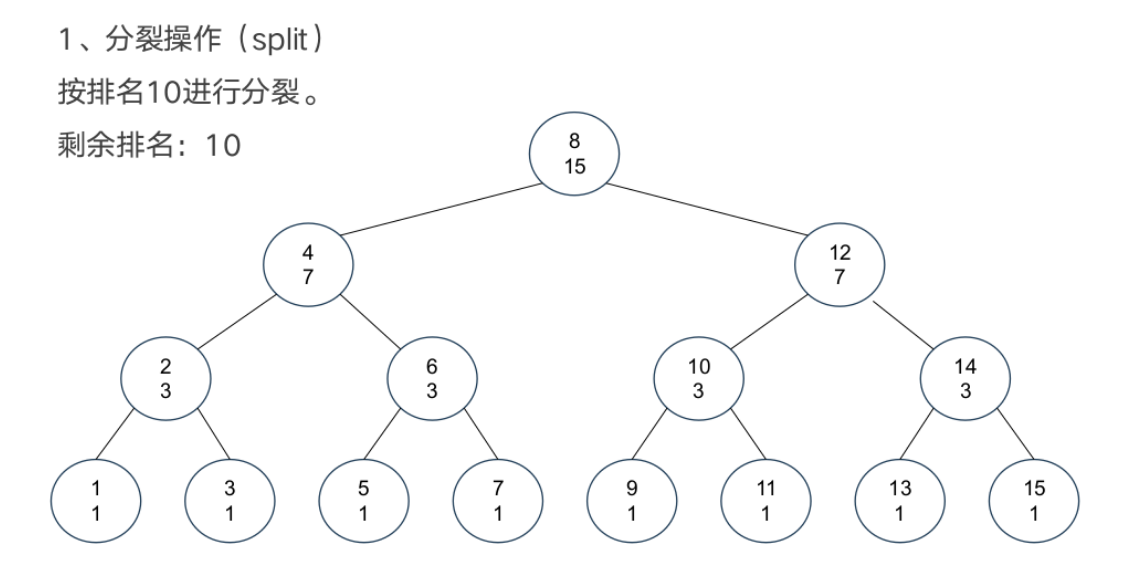
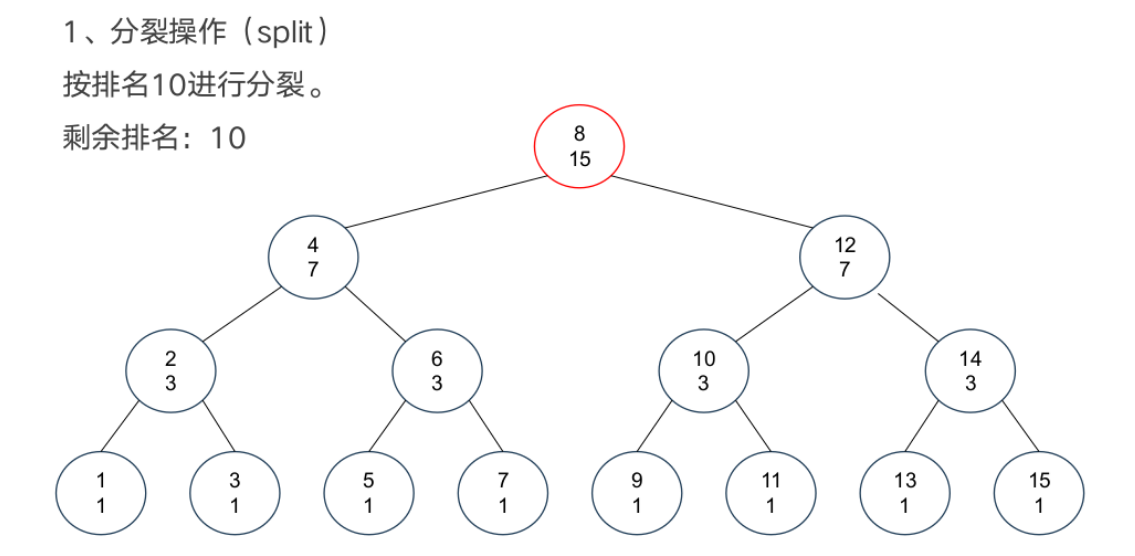
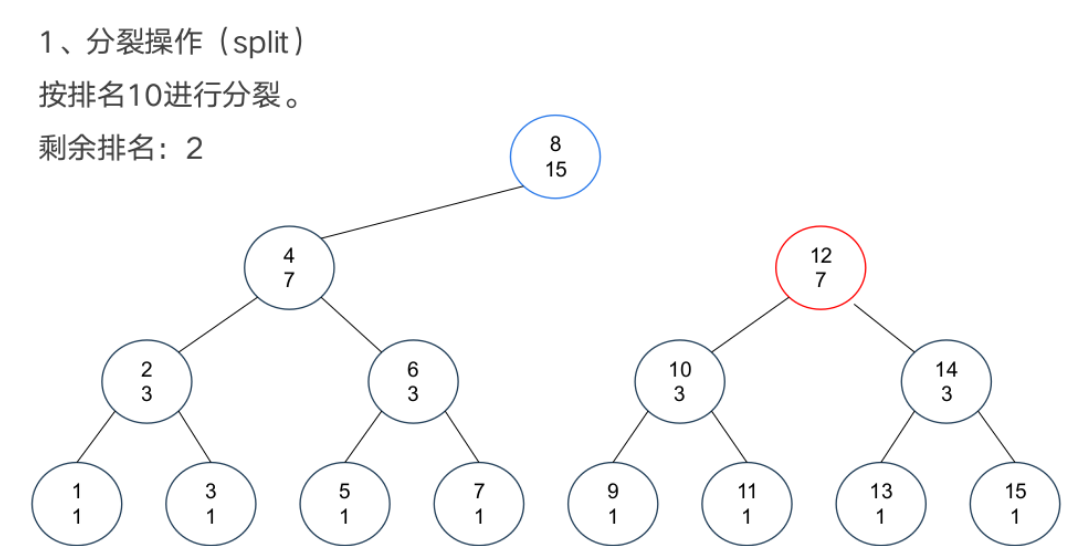
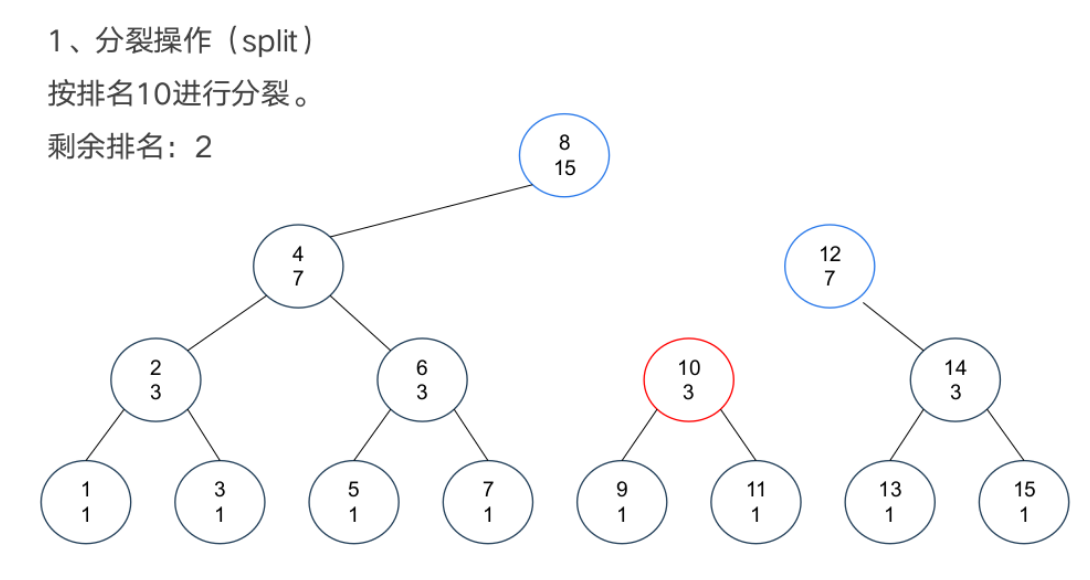
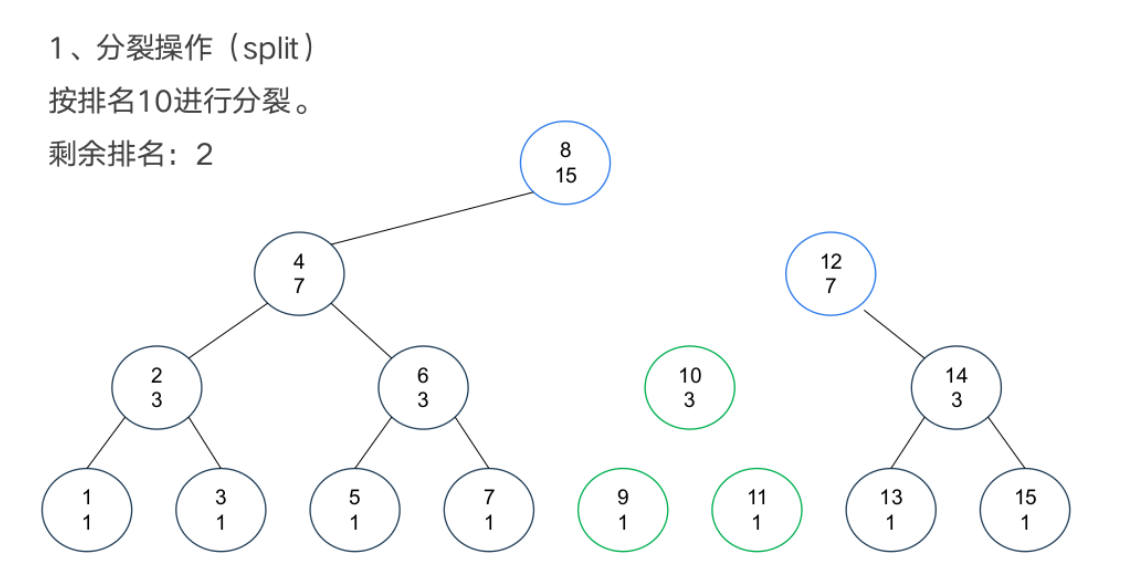
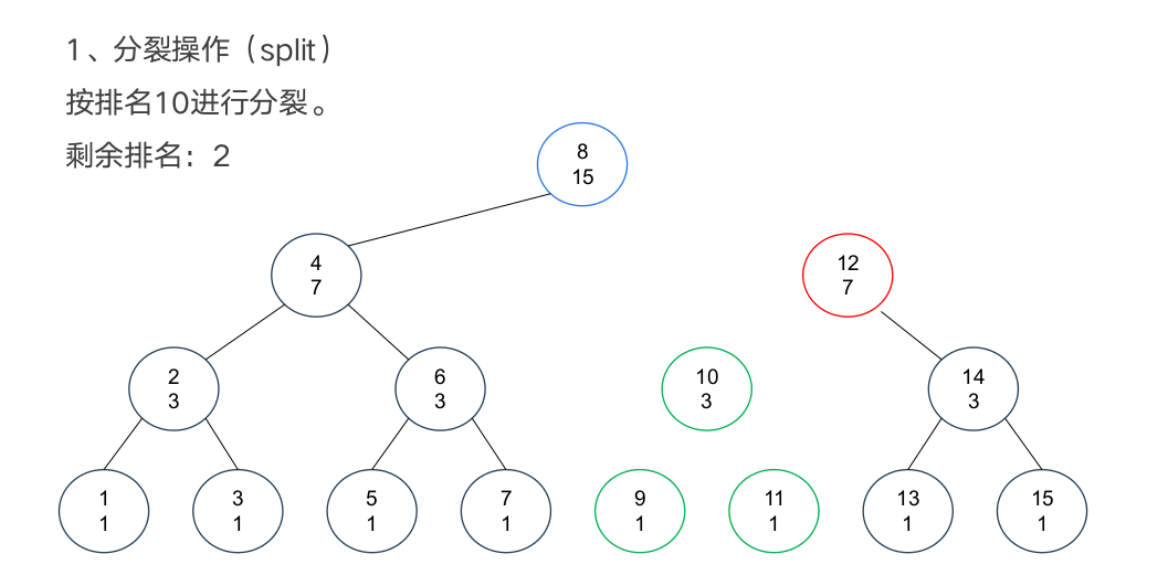
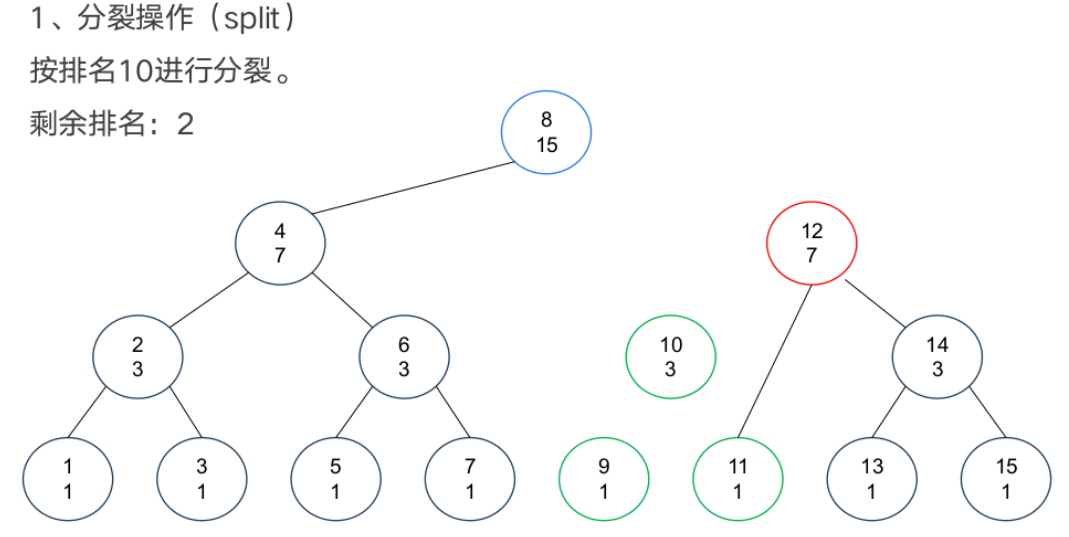
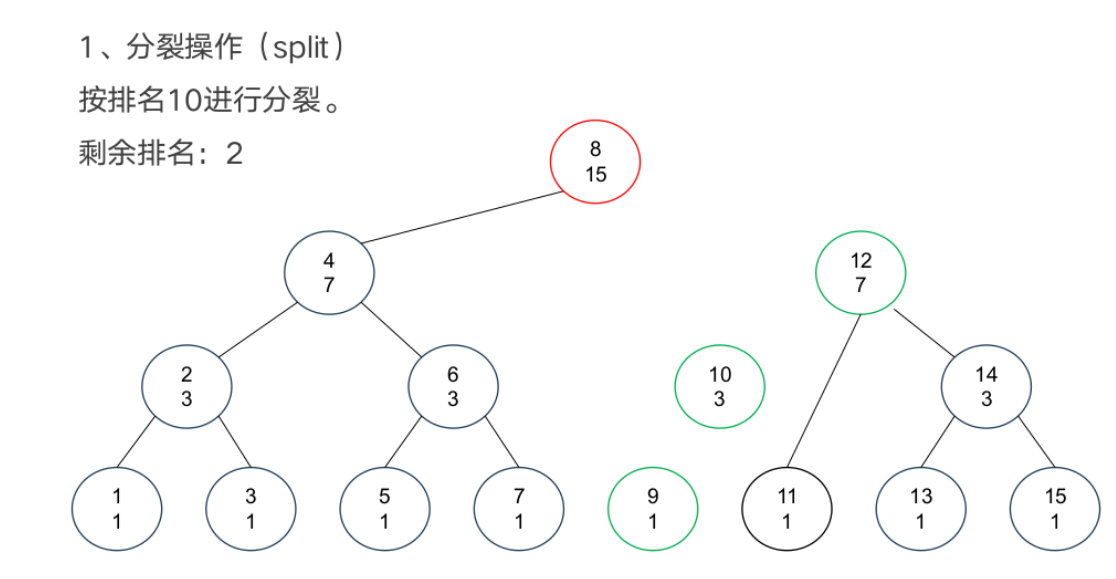
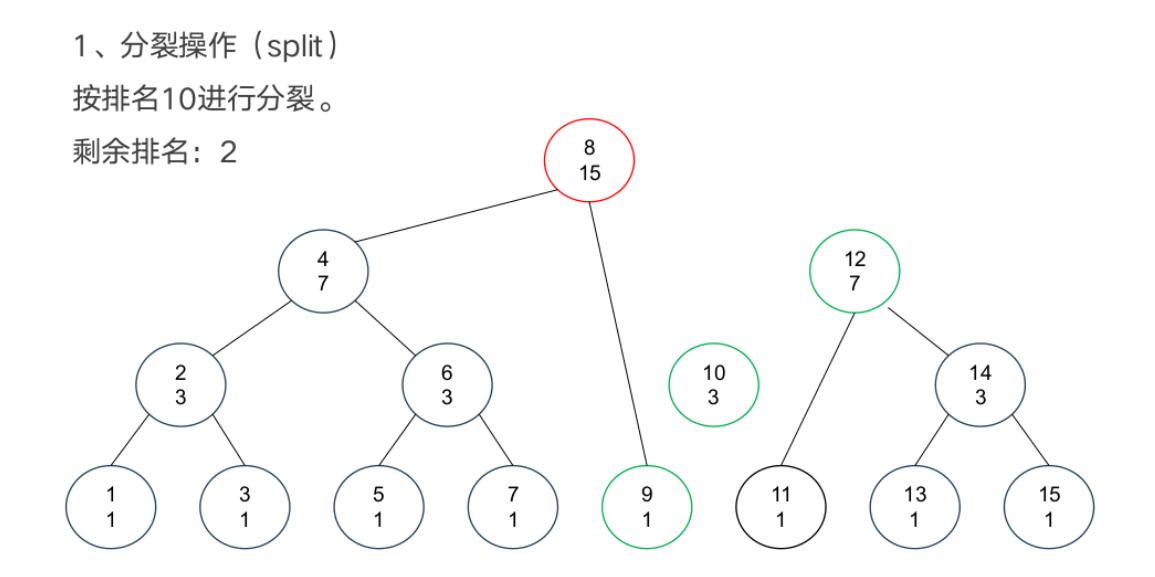
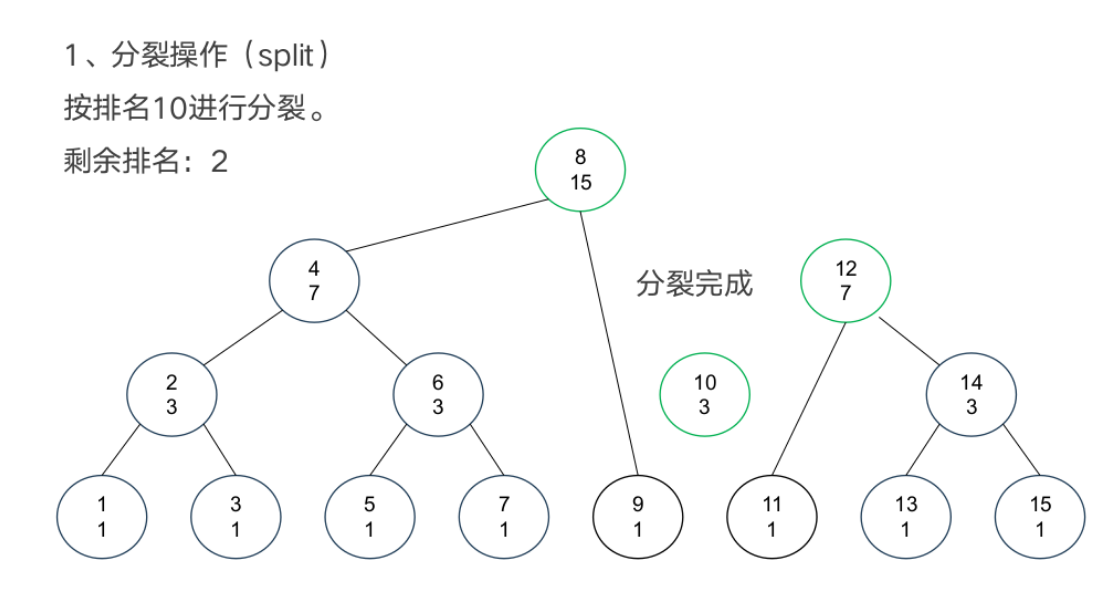
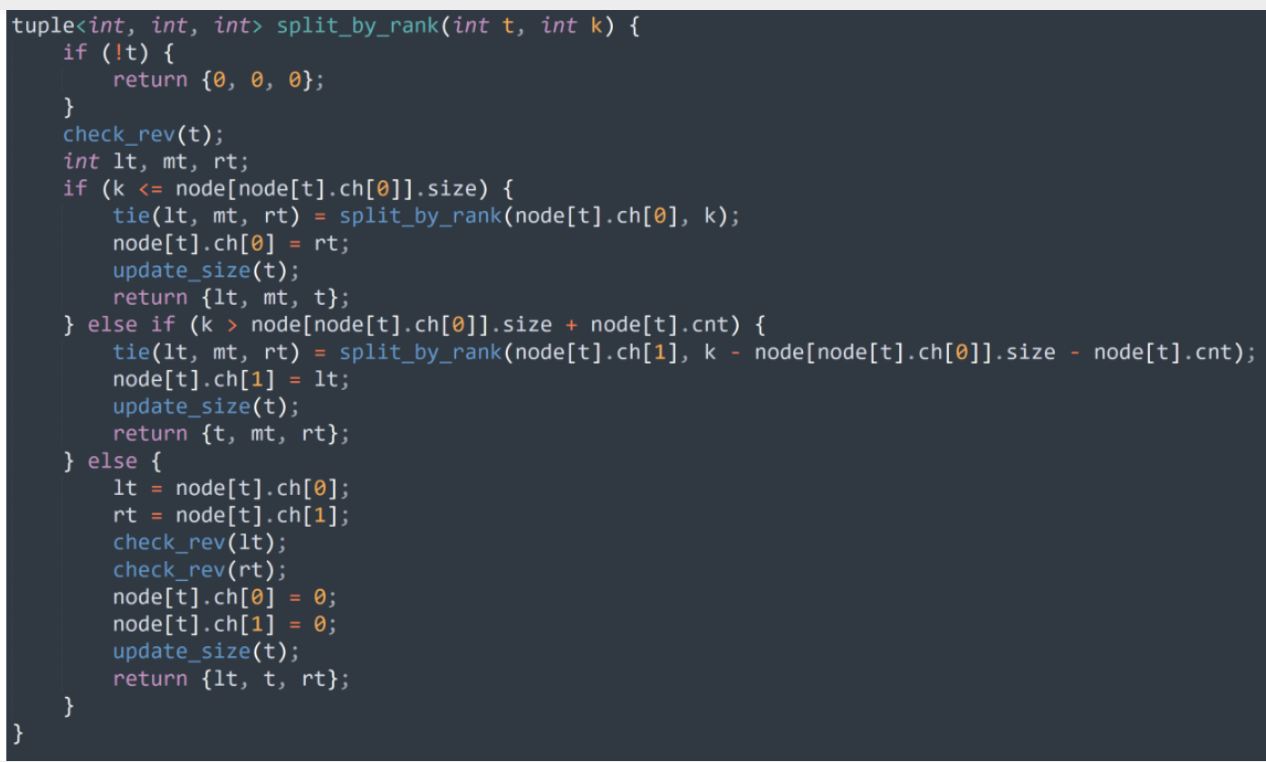

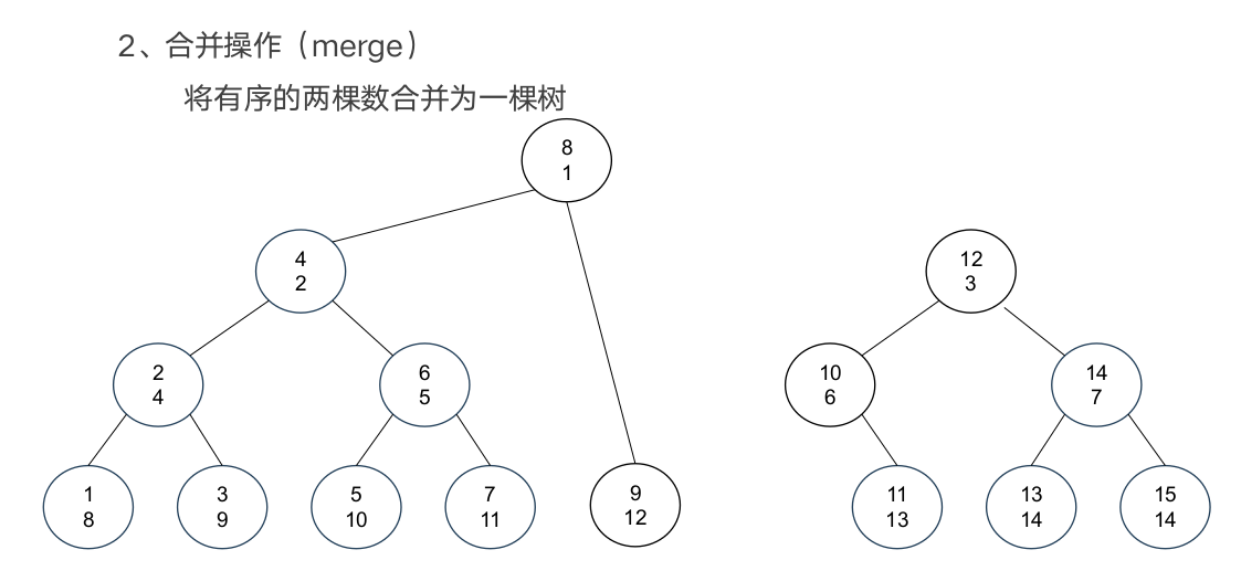
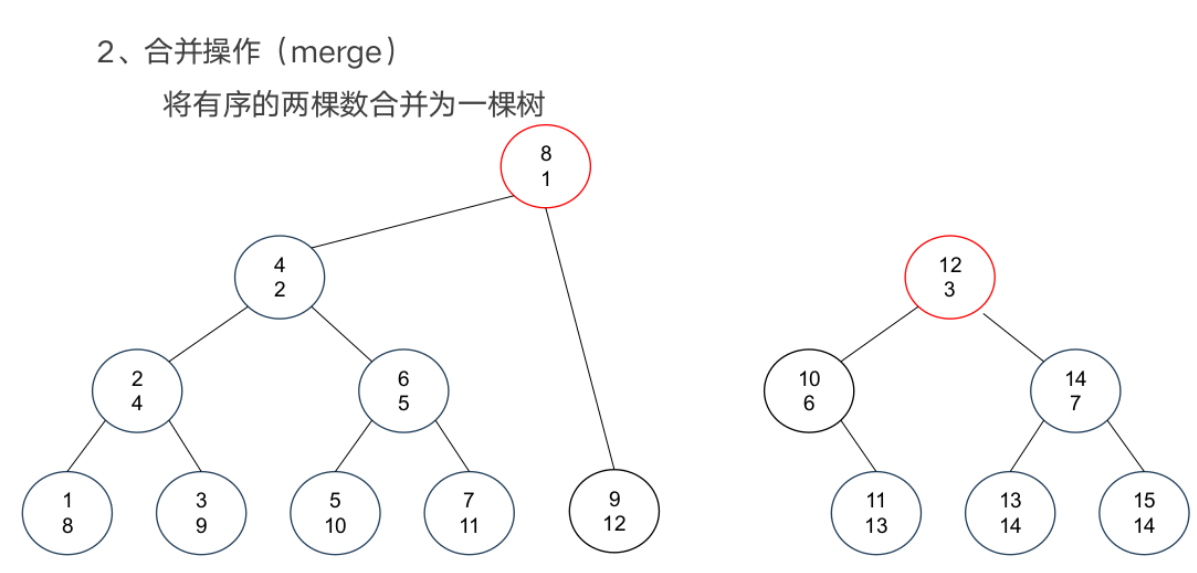
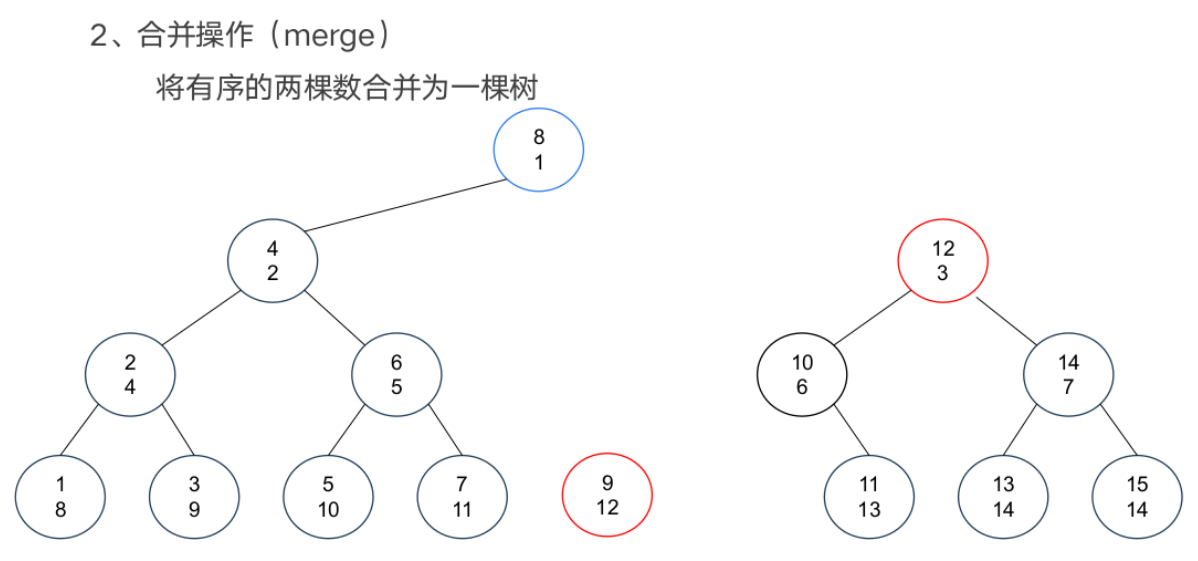
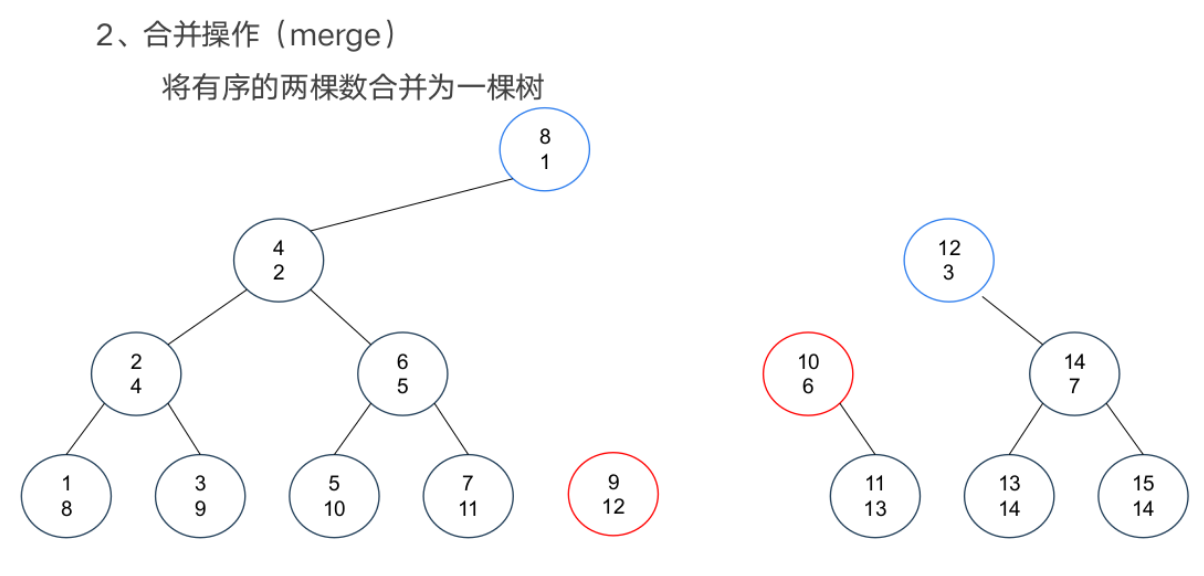

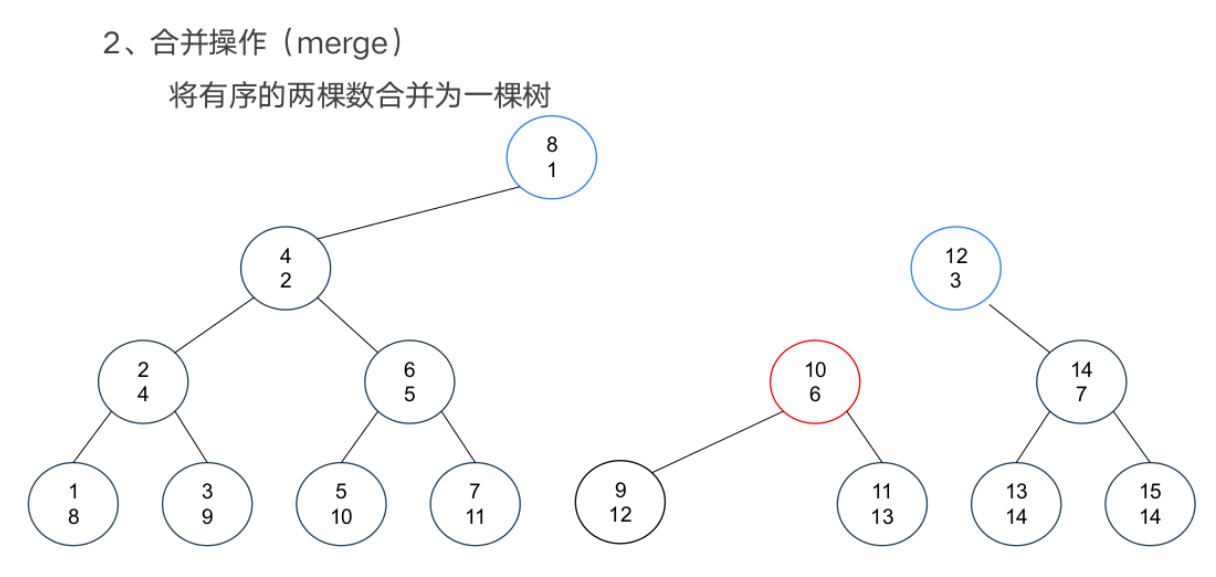

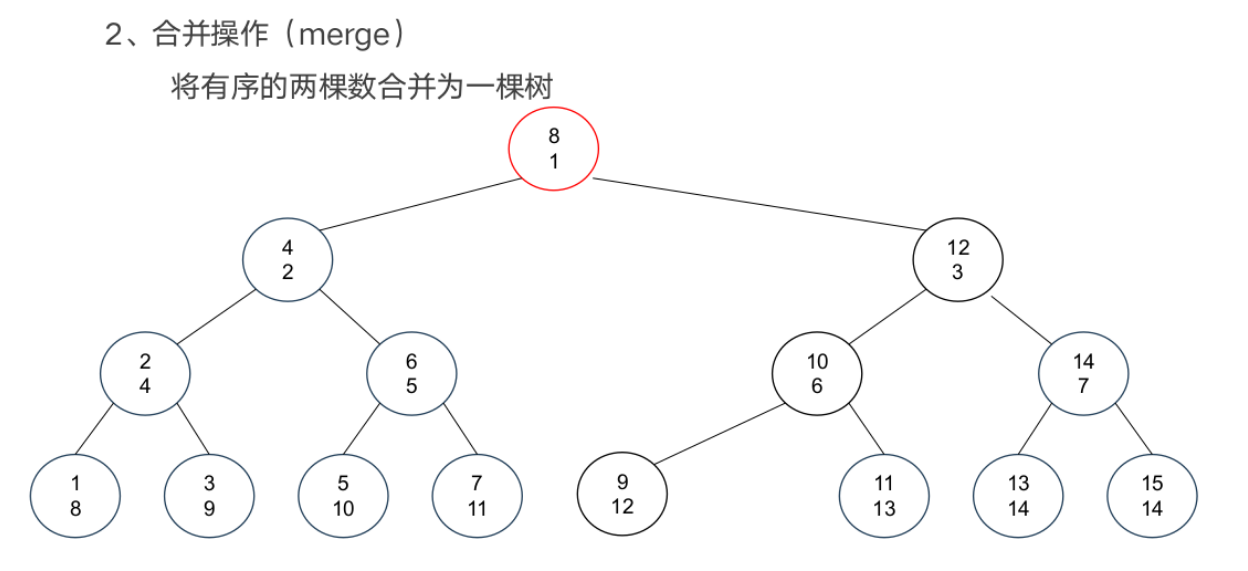

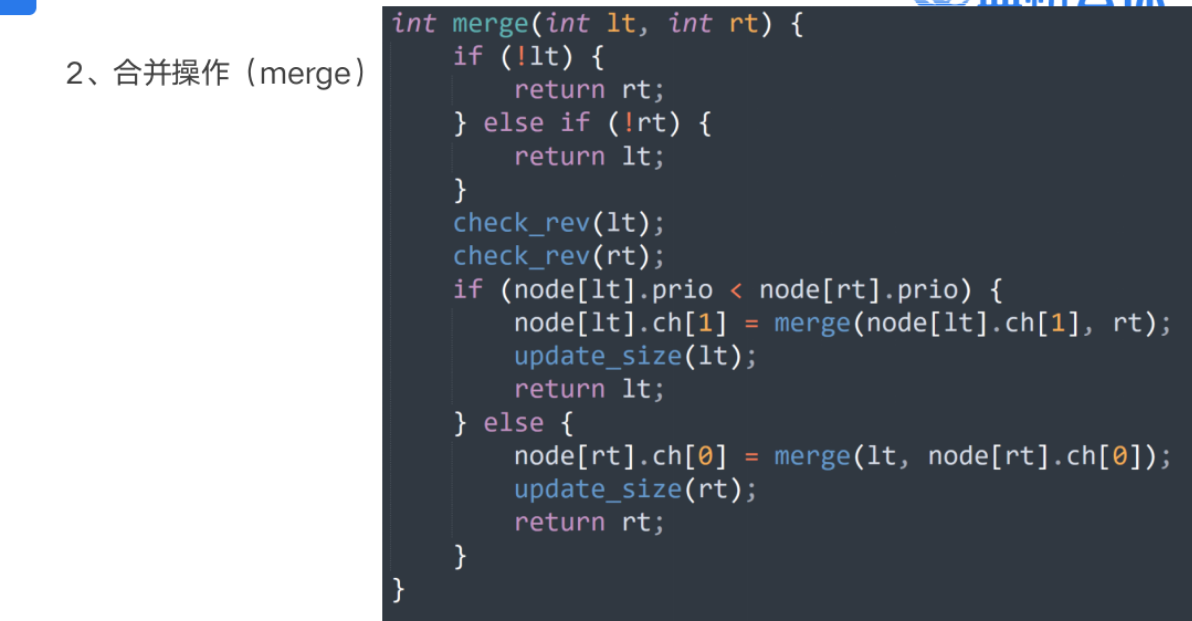

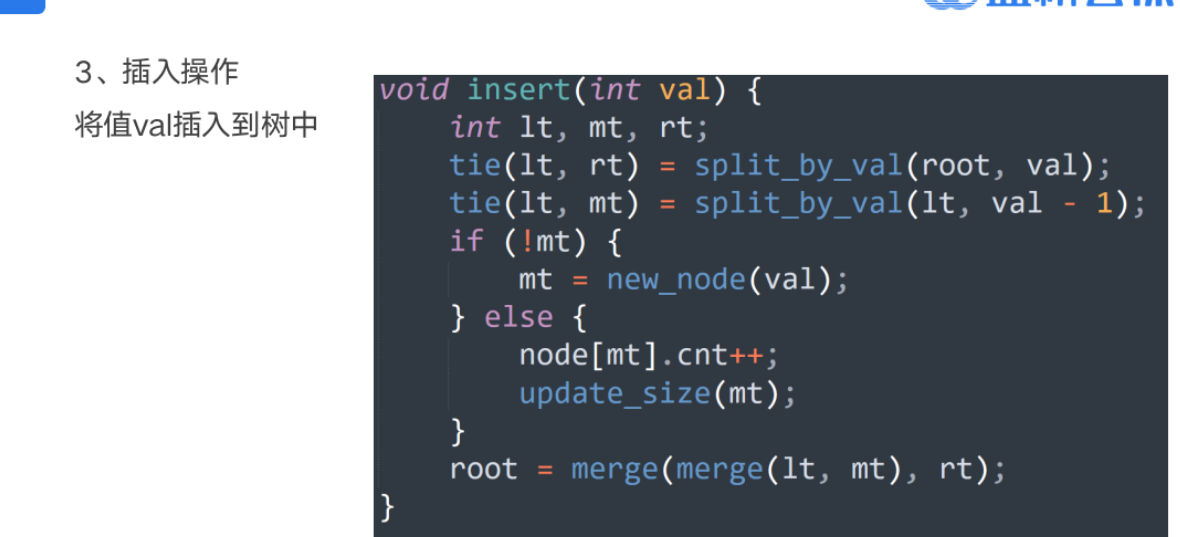







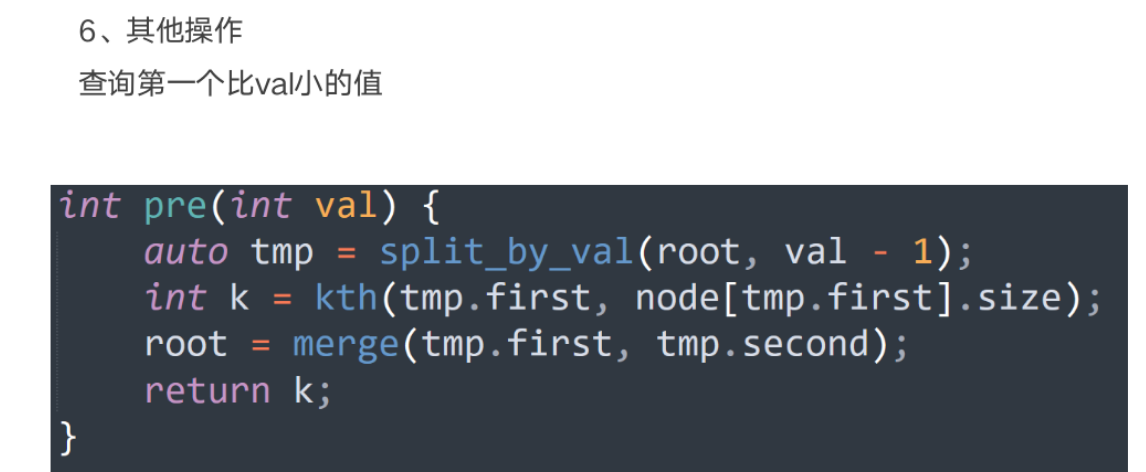


案例
1 | |
单调栈
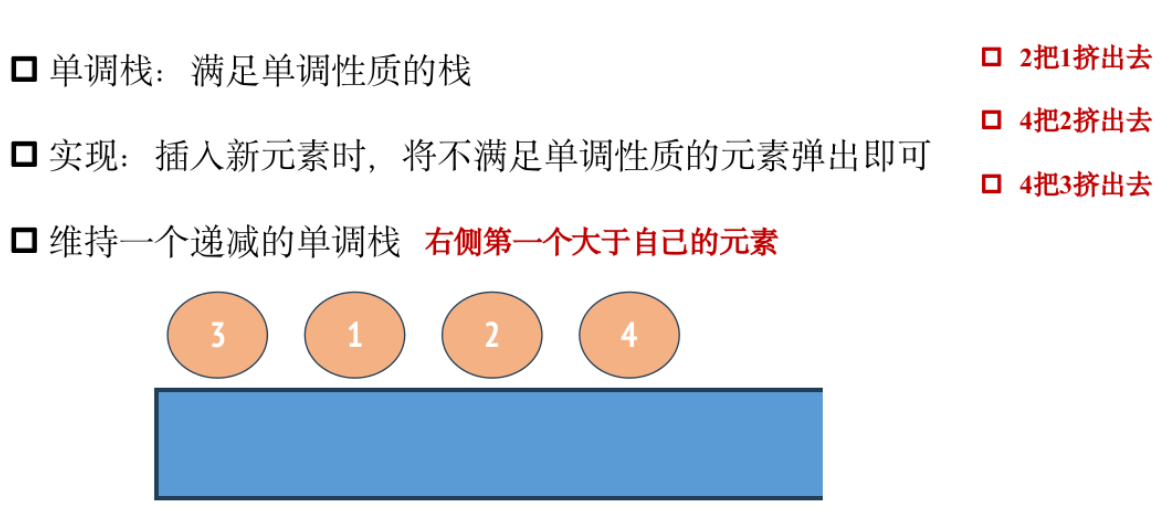

模板题——百亿富翁
1 | |
分块
字符串
KMP&字符串哈希
模式匹配

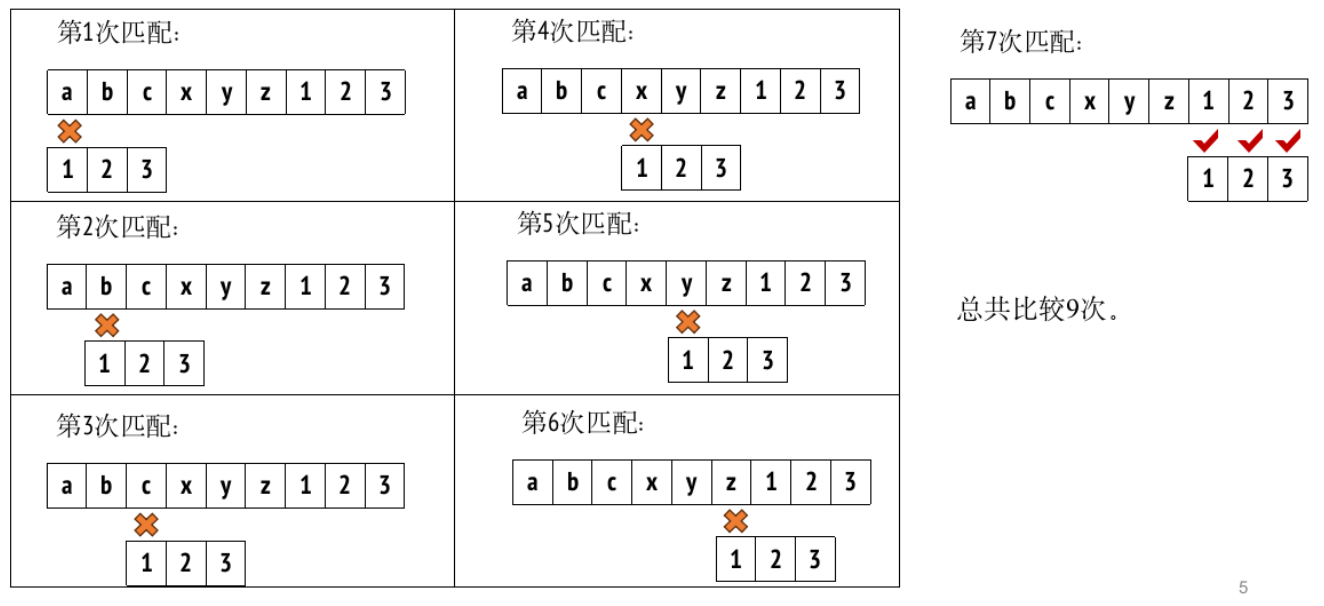
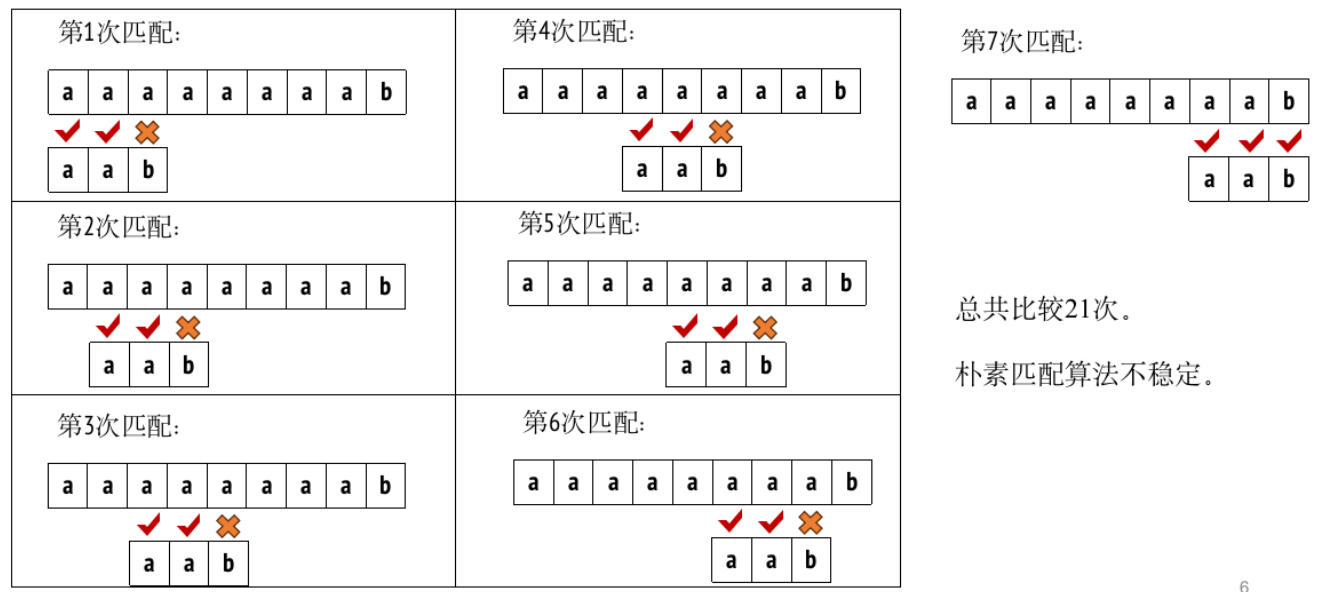
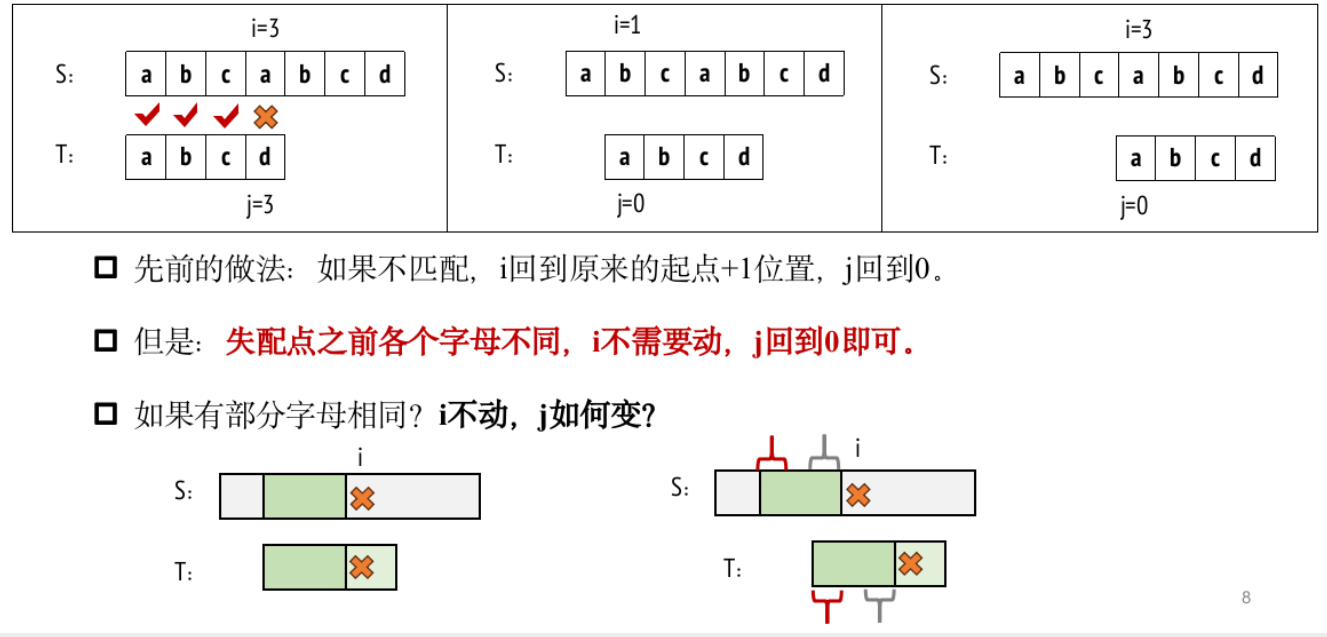
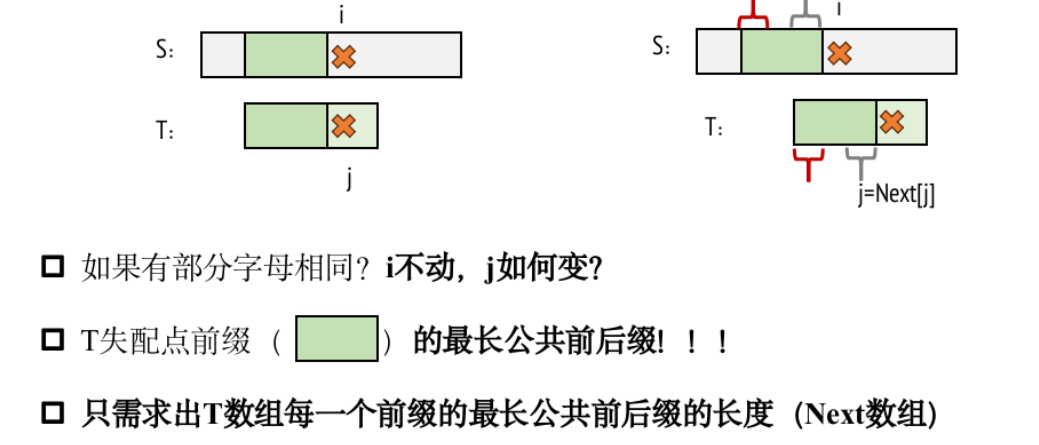
KMP算法
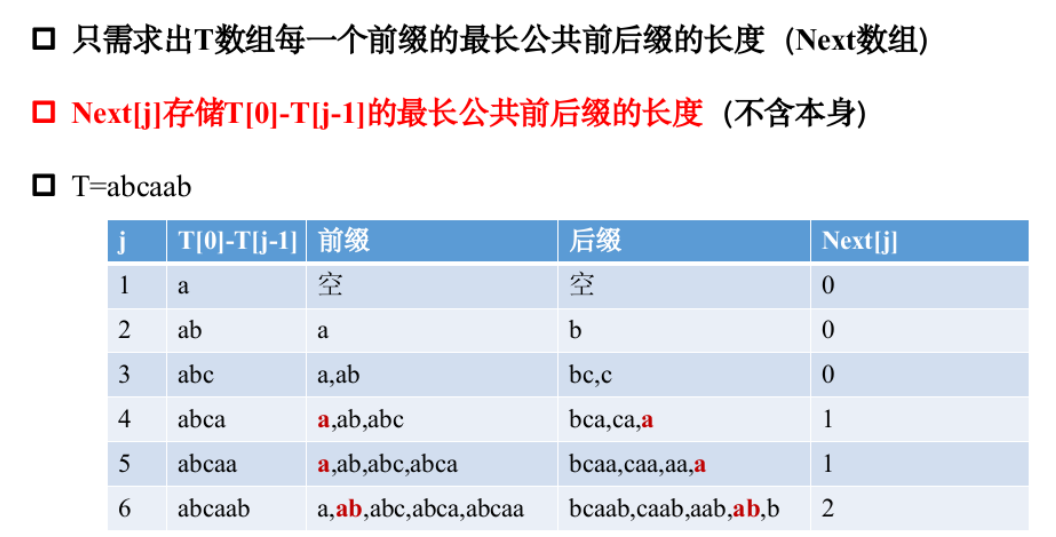

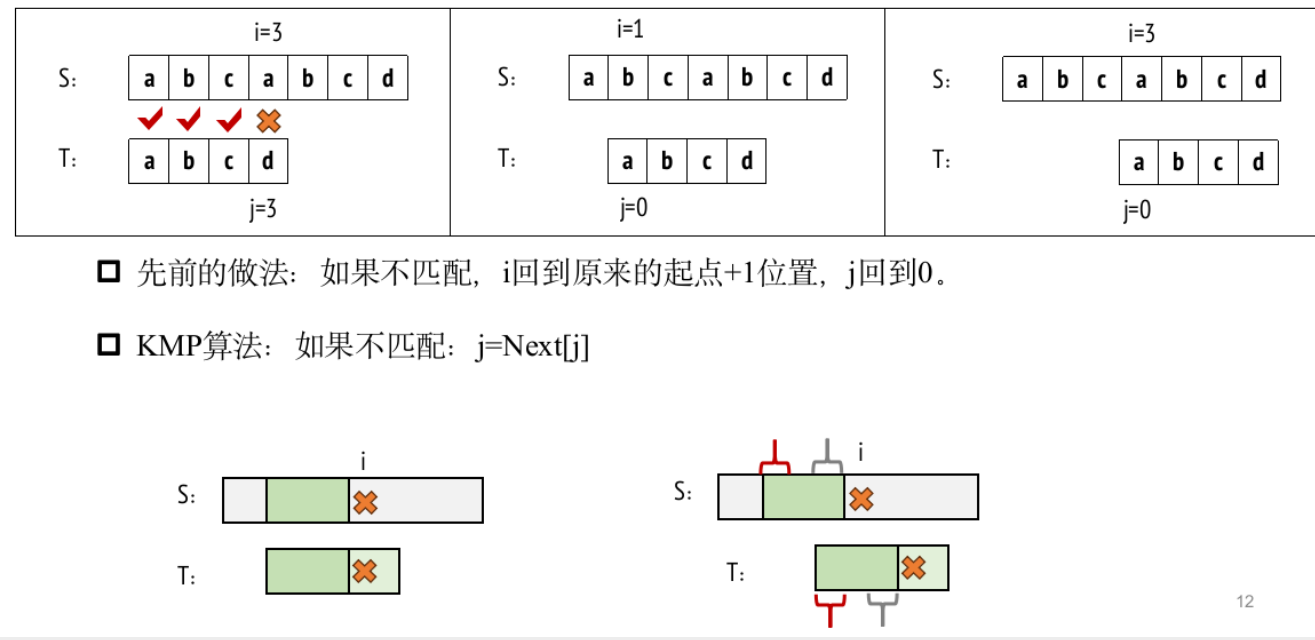
模板题——斤斤计较的小Z
1 | |
1 | |
字符串哈希


模板题——斤斤计较的小Z
1 | |
Manacher


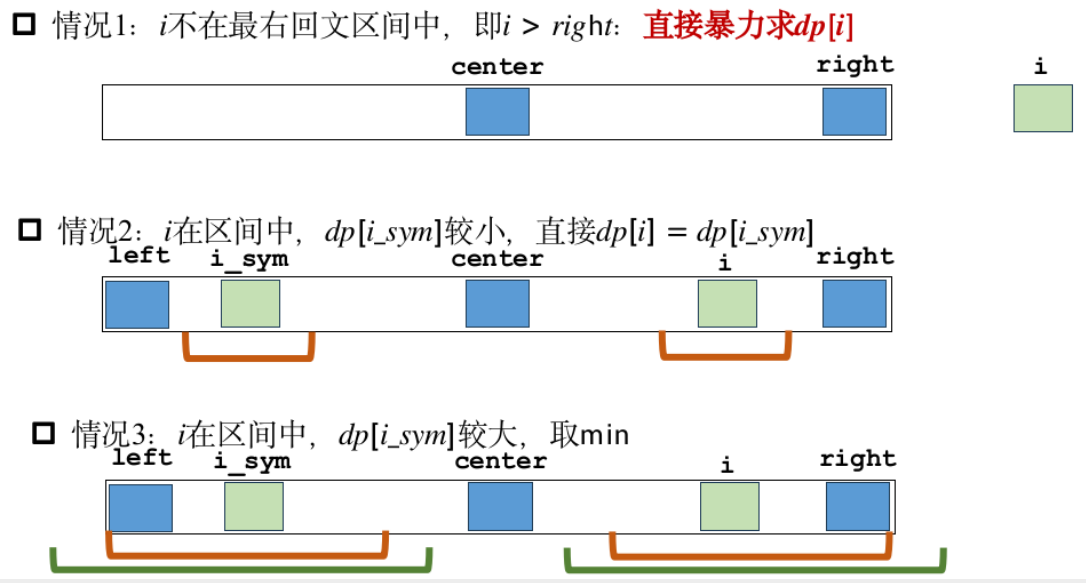

模板

字典树基础
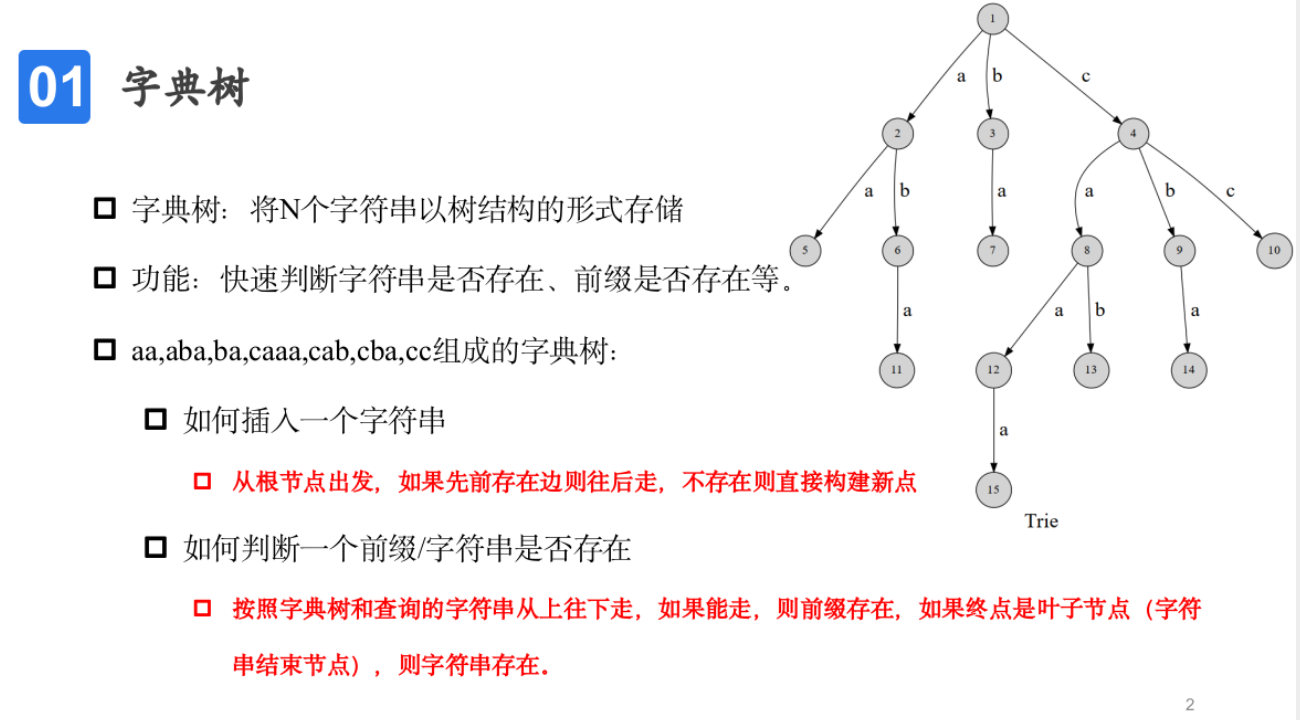
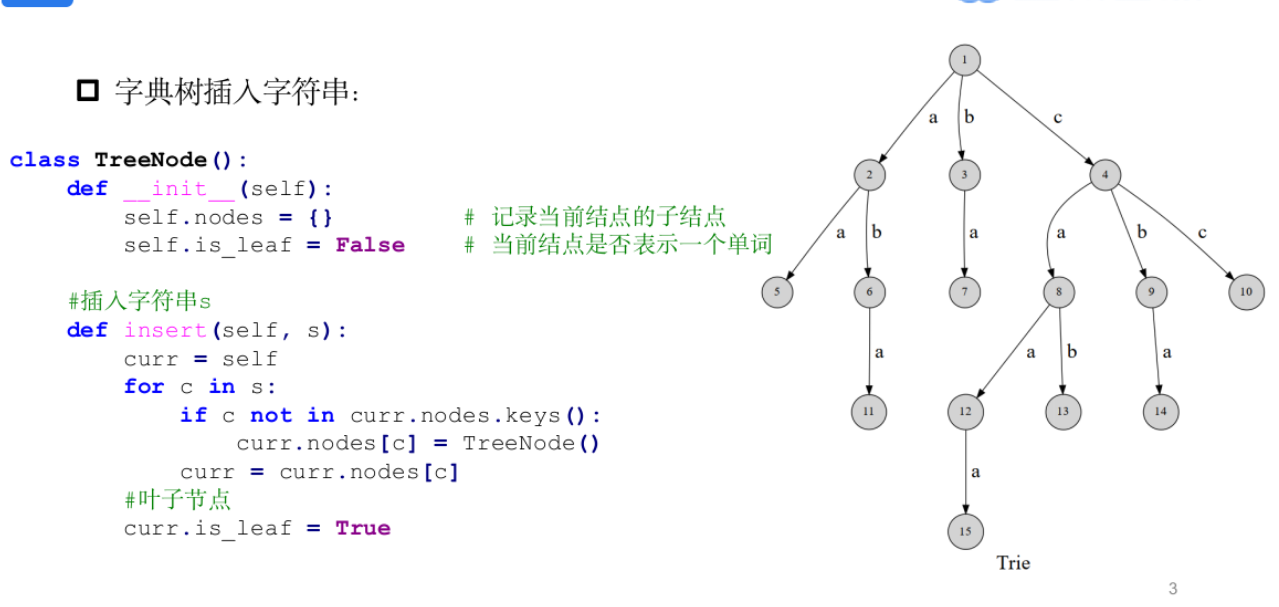
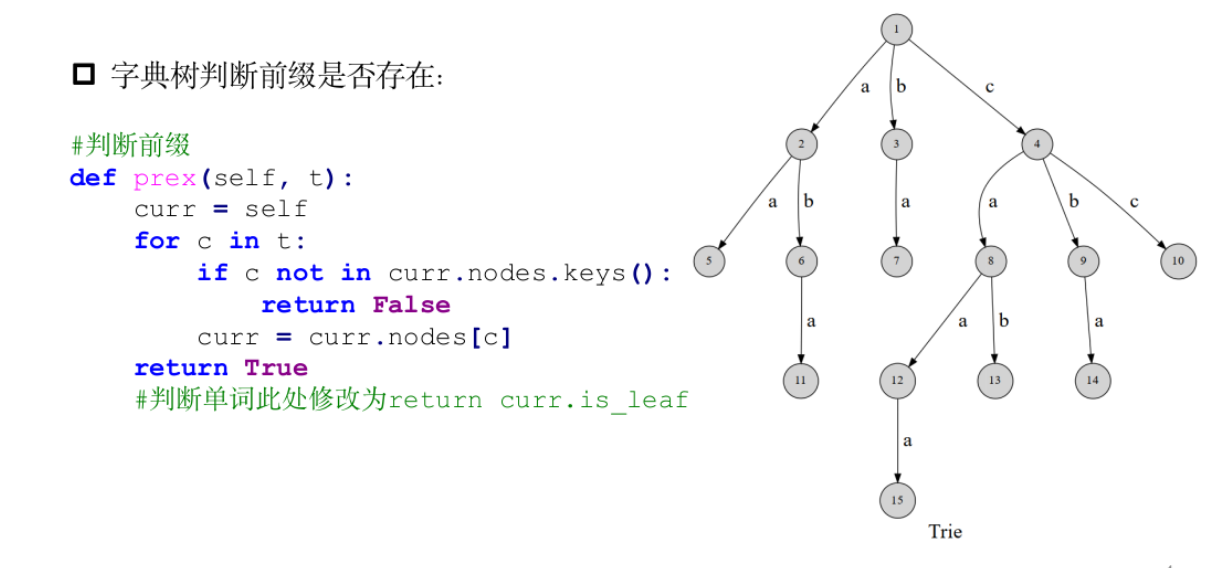
模板题——前缀判定
1 | |
模板题——依依的瓶中信
1 | |
01tire
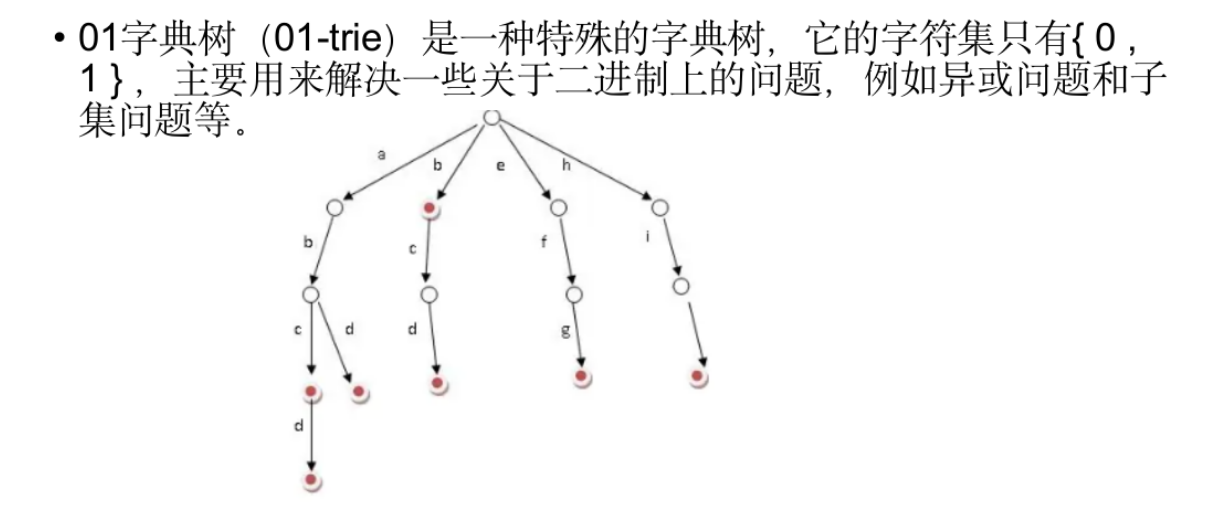





1 | |
图论
基础
基本概念



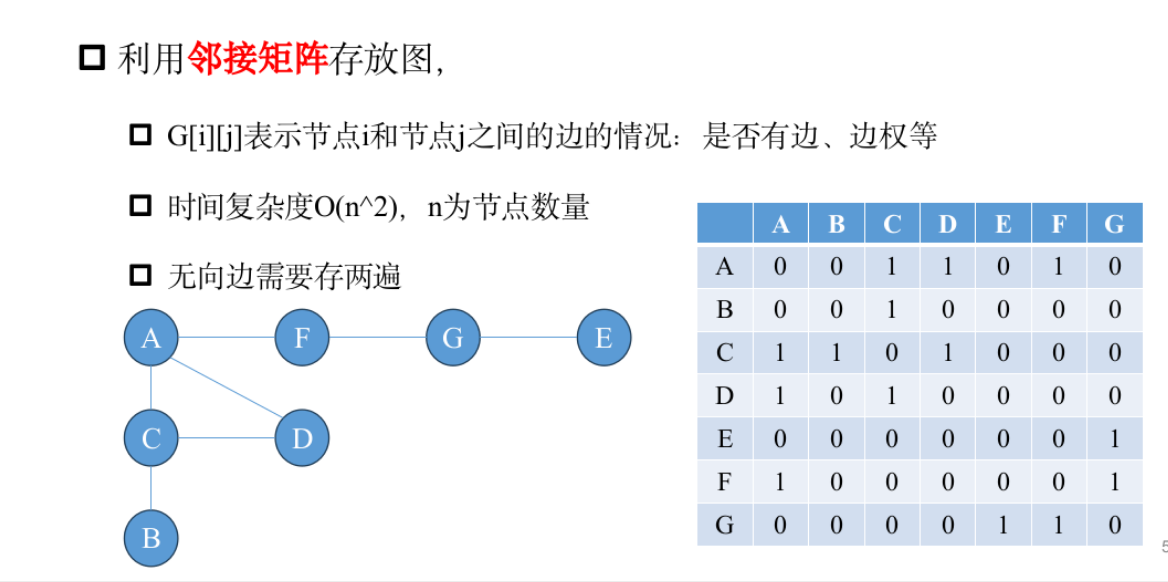
DFS&BFS
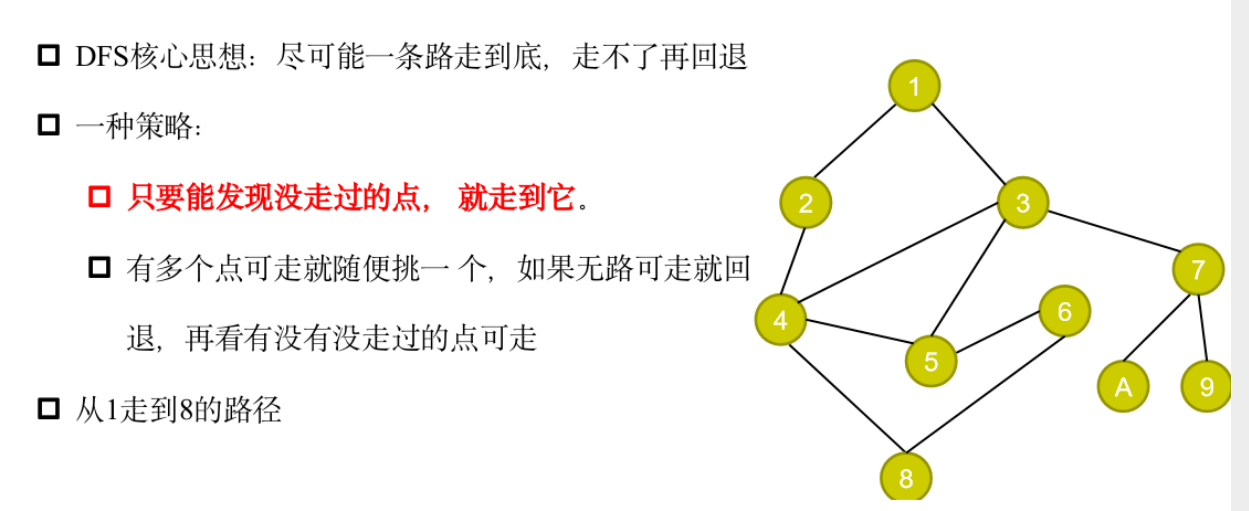
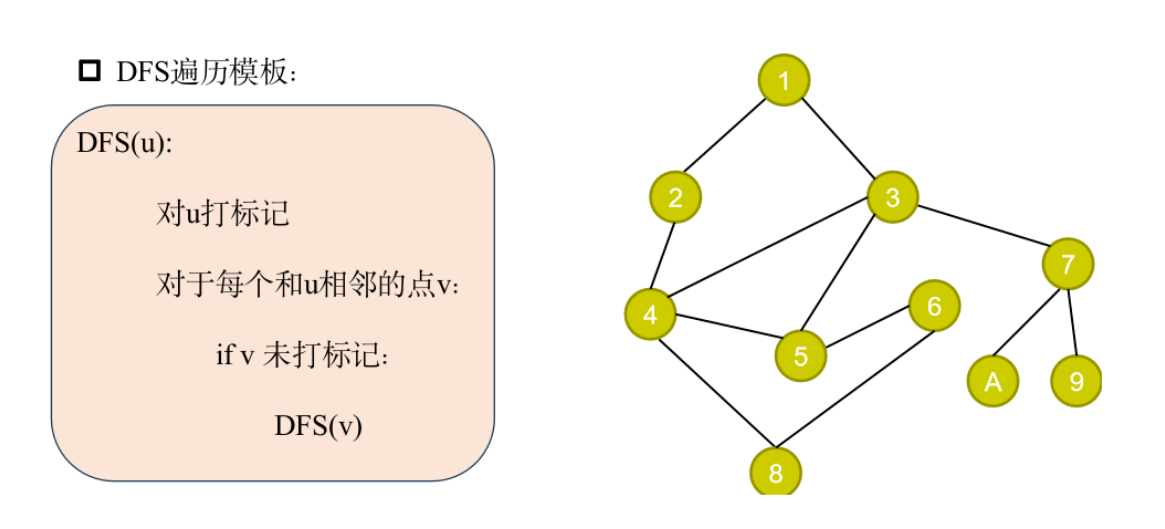
DFS模板题——帮派弟位
1 | |
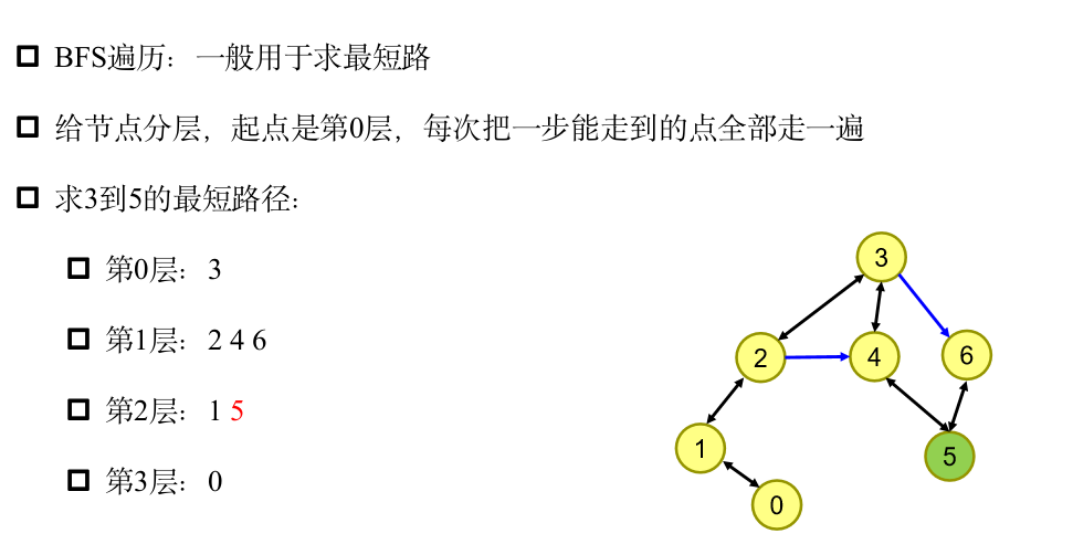

BFS模板题——最少操作数
1 | |
BFS模板题——混境之地4
1 | |
拓扑排序
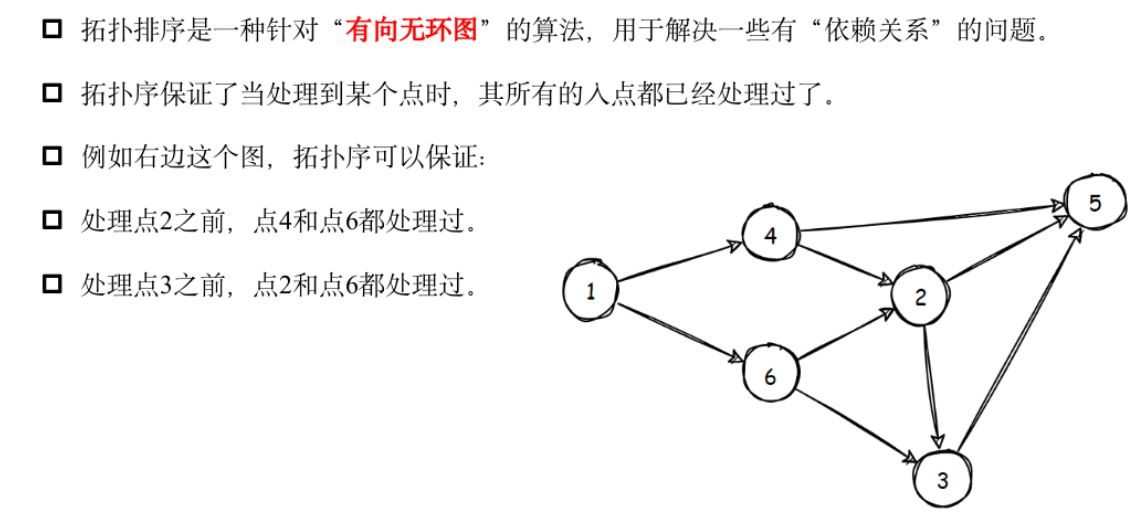
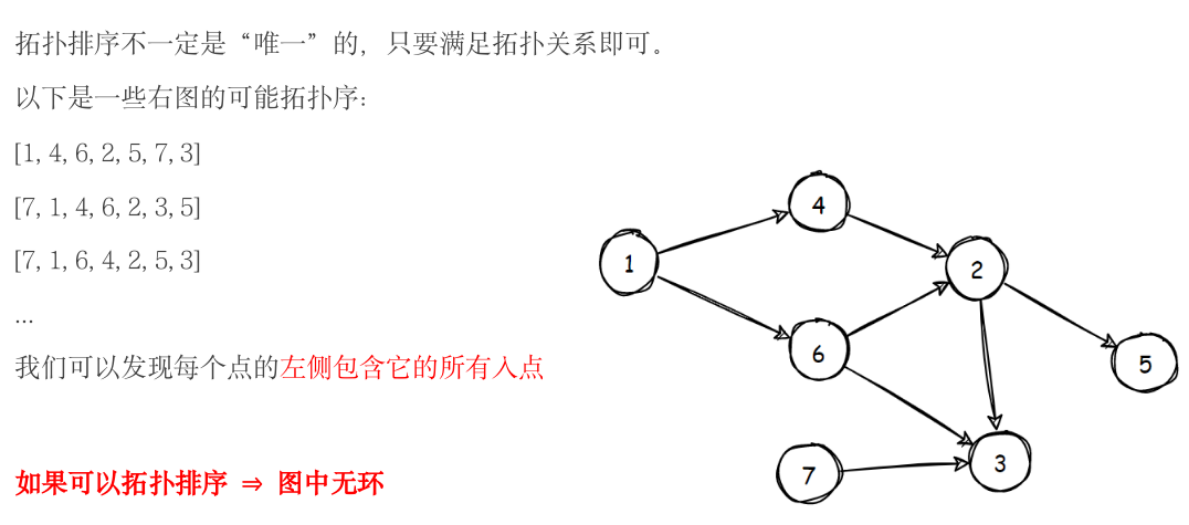

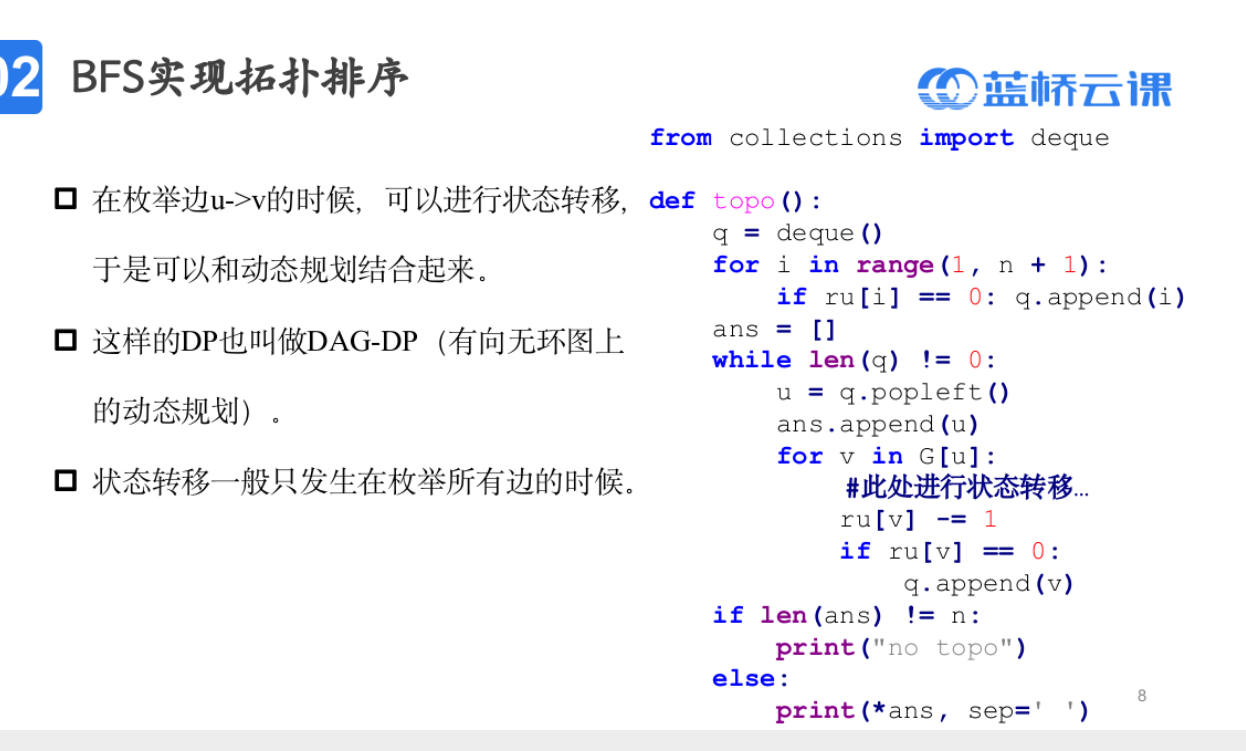
模板题——走多远
1 | |
模板题——最小字典序排列
1 | |
最短路
Floyd


模板题—— 蓝桥公园
1 | |
1 | |
1 | |
模板题——城市间的交易
1 | |
1 | |
Dijkstra
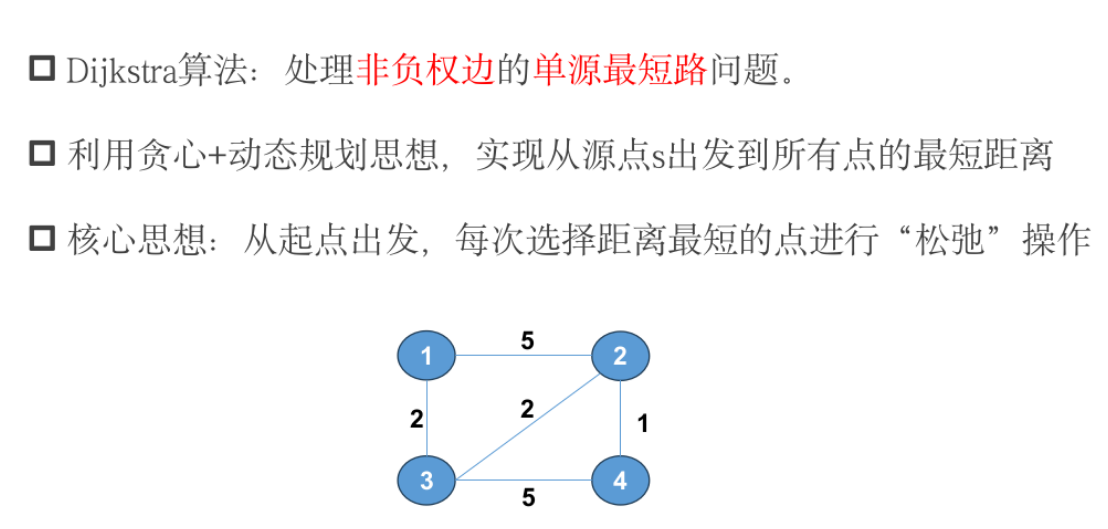

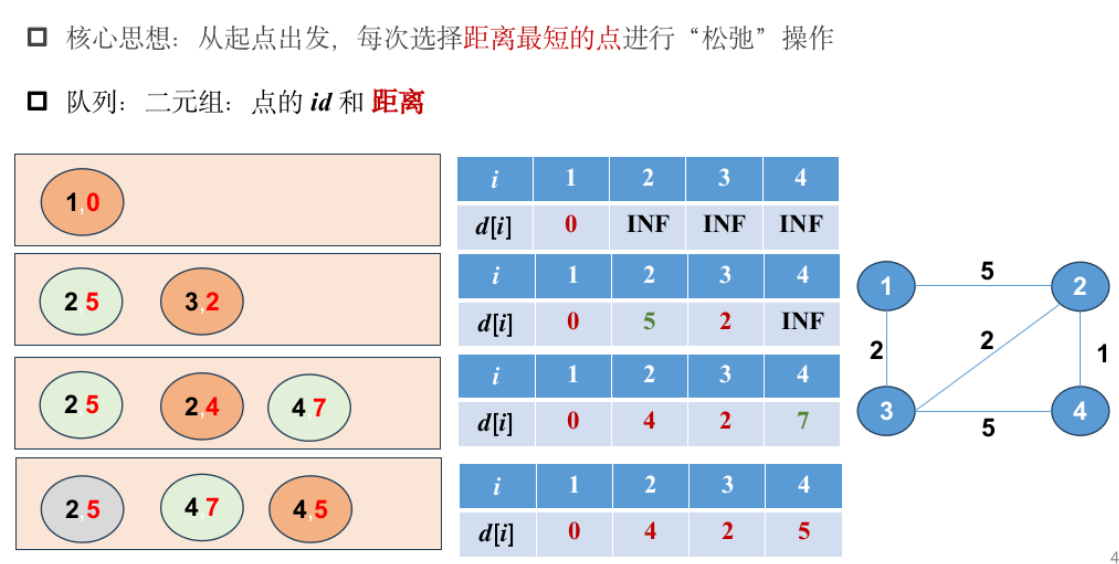
模板题——蓝桥王国
1 | |
模板题——混境之地3
1 | |
生成树
Kruskal
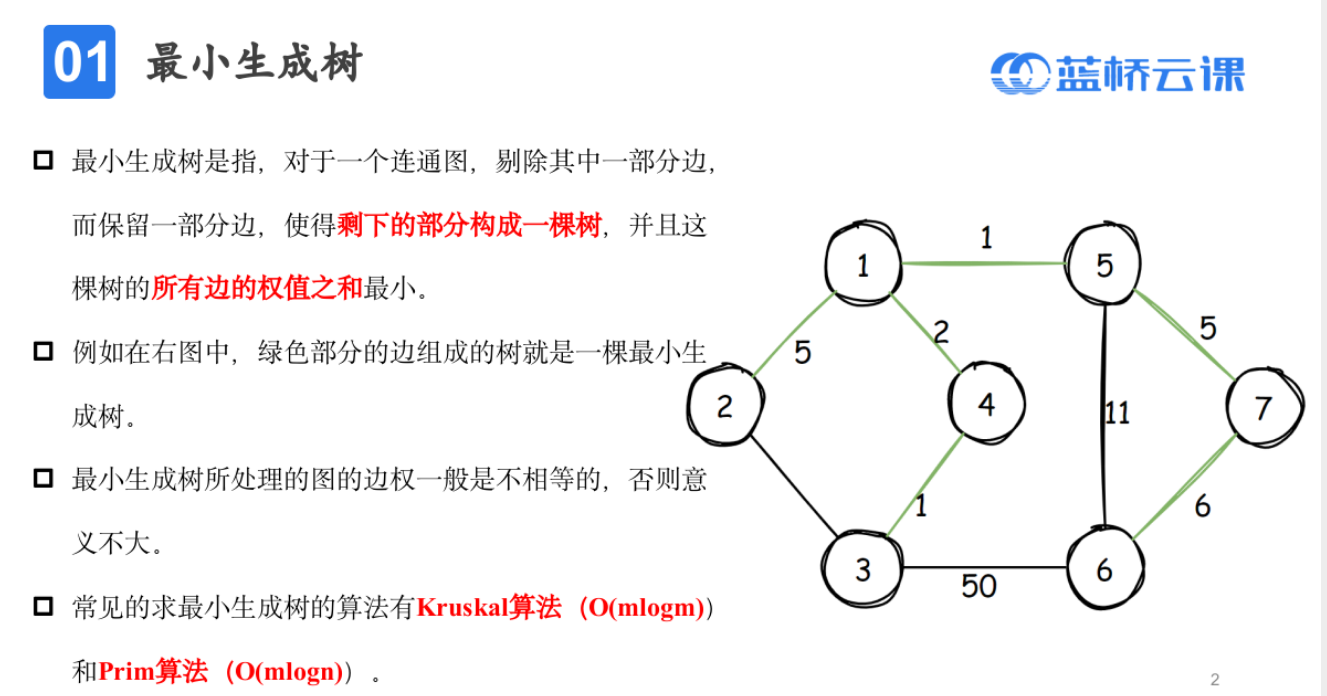
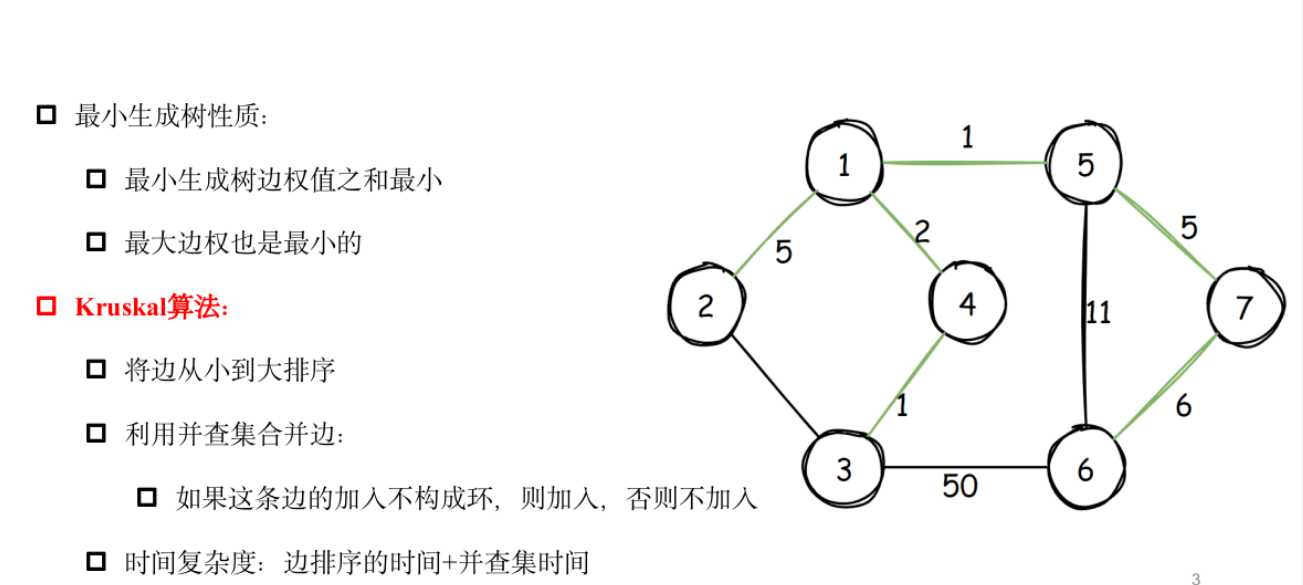
模板题——繁忙的都市
1 | |
Prim
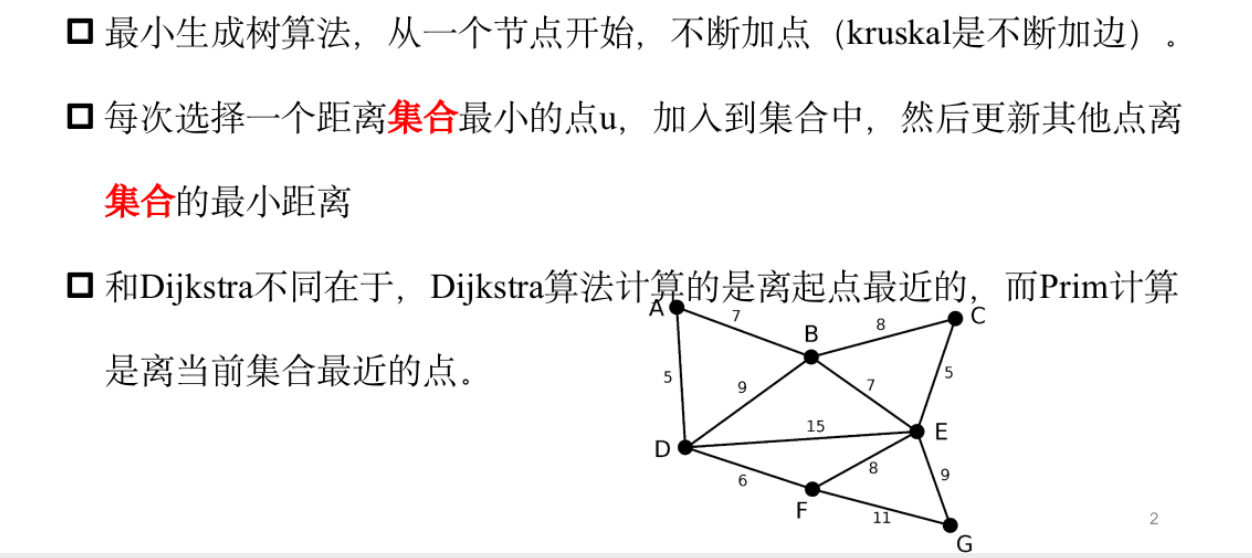
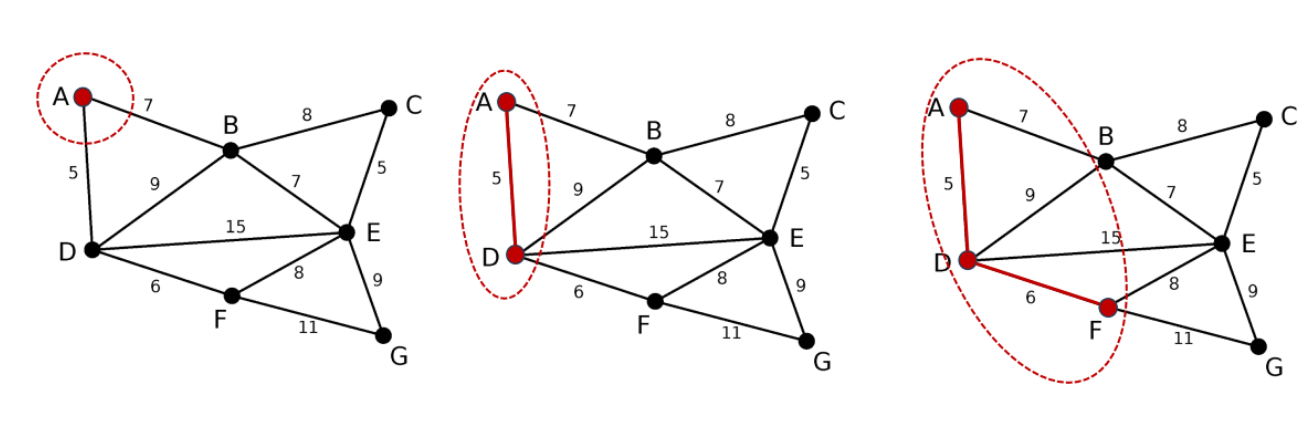
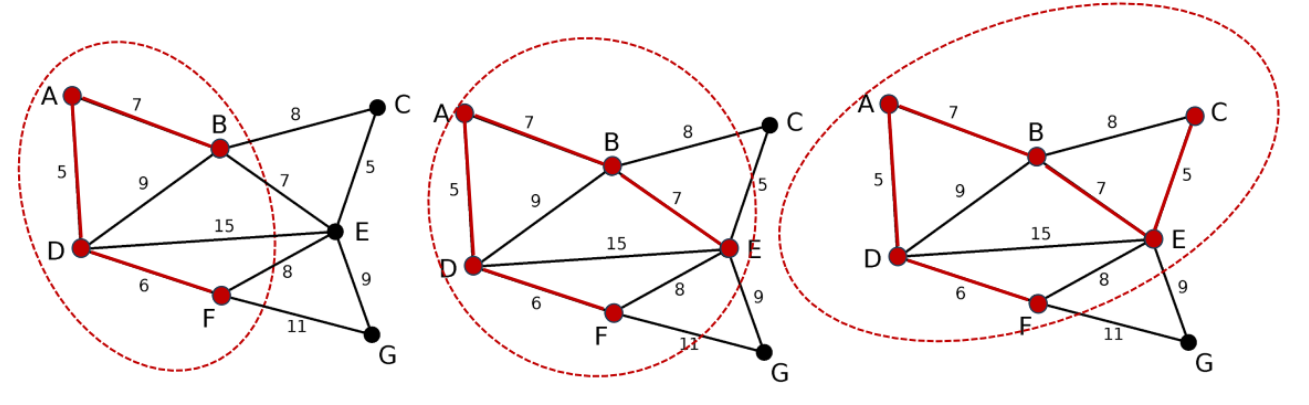
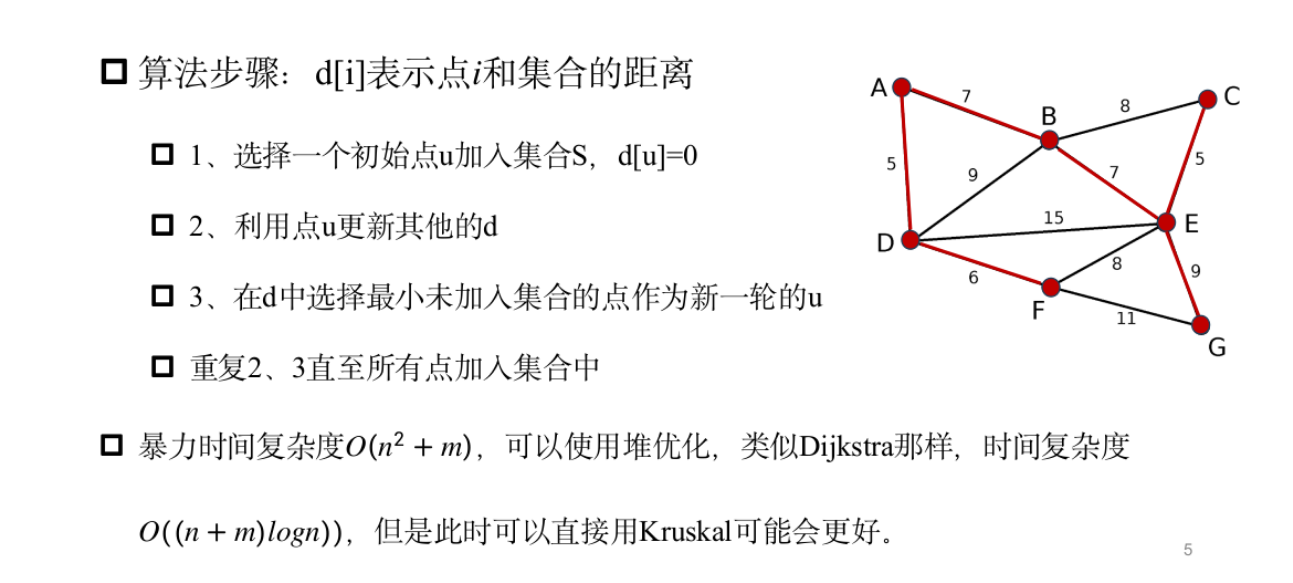
模板题——繁忙的都市
1 | |

打赏
支付宝 | Alipay


微信 | Wechat

